2. Introduction to RL

Roadmap에 있는 내용 가볍게 훑은 후 별도 교안으로 학습

02 강화학습 개념

1. 강화학습 개요

강화학습이란 agent가 environment와 상호작용하며 학습하는 머신러닝의 한 종류. agent는 environment에서 action을 취하고 그에 따른 reward를 받는다.

강화학습의 주요 목적은 기대되는 reward를 증가시키는 policy를 찾는 것이다.

라벨링된 데이터를 바탕으로 이루어지는 supervised learning과는 다르게 RL은 agent가 trial and error 형태로 학습한다.

2. Markov Decision Process

MDP는 decision-making을 모델링하기 위한 프레임워크이다.

state의 집합 $S$ 와 action의 집합 $A$ 그리고 transition model $P(s^{\prime }|s,a)$ 와 reward function $R(s,a,s^{\prime })$ 로 이루어진다.

discounter factor는 미래의 reward에 대한 현재의 가치를 의미한다.

위의 $P$ 와 $R$ 의 함수에서 볼 수 있듯이 다음 state $s^{\prime }$ 는 현재 state $s$ 와 action $a$ 에 의해 결정되며 reward는 $s\to s^{\prime }$ 로의 이동에서 발생한다.

3. 가치함수(상태-가치, 행동-가치)

• State-Value Function V(s): state $s$ 에서 미래까지 최적으로 얻을 수 있는 reward를 의미한다. 따라서 agent가 특정 $s$ 에 있는 것이 얼마나 좋은지 나타낸다.
• Action-Value Function Q(s,a): $s$ 에서 $a$ 를 취했을 때의 미래까지 최적으로 얻을 수 있는 reward를 의미한다. 따라서 주어진 $s$ 에서 취하는 각 $a$ 의 중요도를 나타낼 수 있다.

4. 벨만 방정식 (Bellman Equation)

RL의 기본 원칙으로 각 state와 다음 state(또는 action) 간의 관계를 나타낸다. 최적값 함수를 계산하는데 사용된다.

$$\begin{gathered} V(s)=\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V(s^{\prime })] \\ Q(s,a)=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \sum _{a^{\prime }}\pi (a^{\prime }|s^{\prime })Q(s^{\prime },a^{\prime })] \end{gathered}$$

State-Value Function V(s)에 대해 자세히 살펴보자.

$\pi$ 는 policy이다. 따라서 이 policy에 대해 $s$ 에서 취할 수 있는 모든 $a$ 를 합한 것이 ${\sum }_a\pi (a|s)$ 이다.

$p(s^{\prime },r|s,a)$ 는 $s$ 에서 $a$ 를 취했을 때의 이동할 $s’$ 와 얻을 $r$ 에 대한 확률이다. 여기에 얻은 reward $r$ 과 미래의 얻을 $V(s’)$ 에 대해 discount factor를 곱하였다.

정리하자면 특정 state $s$ 에서 policy에서 취할 수 있는 action $a$ 를 통해 얻을 수 있는 모든(미래까지) reward $r$ 을 계산하는 함수이다.

마찬가지로 Action-Value Function Q(s,a)도 동일하게 생각해볼 수 있다.

이번에는 특정 state $s$ 에서 취한 어떤 $a$ 에서 얻을 수 있는 reward $r$ 을 모두 계산한다. discount factor를 곱해 다음 state $s’$ 에서 갖게되는 모든 value 들도 연쇄적으로 포함하고 있다.

5. 몬테카를로, TD (Monte Carlo and Temporal Difference Learning)

• Monte Carlo(MC): 몬테카를로는 episodes로 부터 바로 학습한다. environment의 모델링의 영향을 받지 않는다(model-free). 여러 랜덤 샘플링을 통해 return 값을 얻어내 이를 통해 값을 추정한다.
• Temporal Difference(TD) Learning: Dynamic programming(DP)와 Monte Carlo 를 결합한 것이다. episode가 끝날 때까지 기다리지 않고, 추정값을 다른 학습된 값으로 업데이트한다. 이러한 방식은 연속적인 task의 환경이나 최종값을 바로 알기 어려운 환경에서 사용하기 적합하다.

Reinforcement vs Supervised vs Unsupervised Learning

각각의 차이를 알아보자.

RL은 처음 설명한 것과 같이 시간에 따라 누적되는 기대 reward를 증가시키는 policy를 찾는 것이다.

Supervised Learning은 input data를 기대되는 ouput으로 mapping할 수 있도록 학습하는 것이다. 이때 data는 라벨링된 train data를 사용한다.

Unsupervised Learning은 라벨링되지 않은 data로부터 숨겨진 패턴이나 구조를 찾아내는 것이다.

주로 RL은 action에 대해 정해진 reward를 가지고 학습한다.

Supervised는 학습시킬 각 dataset에 정답이 주어진다. 학습 시킨 후 test data에 대해 정답을 잘 맞추도록 하는 것

Unsupervised는 라벨링이 없이 data들이 이루고 있는 규칙적인 혹은 반복되는 특징들을 찾아내는 것

---

Markov Decision Process, Value Iteration and Policy Iteration

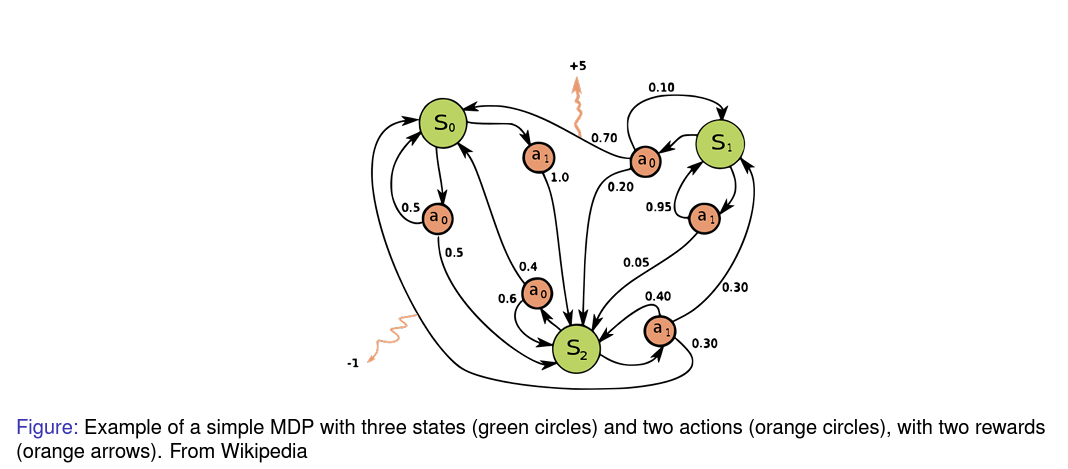
MDP는 강화학습에서 완전히 관측가능한(fully observable) environment를 의미한다. 거의 대부분의 RL 문제들은 MDP로 표현할 수 있다.

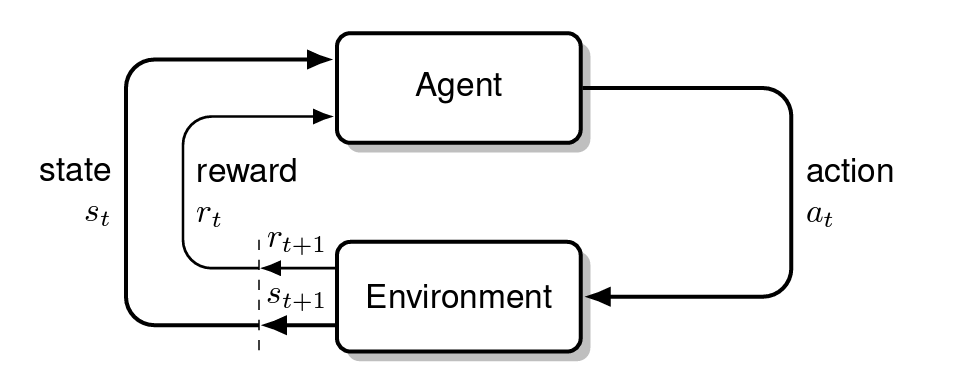
Agent는 학습하는 대상이면서 결정을 내린다(learner and decision-maker)

Agent 외의 상호작용 하는 모든 것들을 environment라고 한다. agent는 action을 선택하고 environment는 이에 대해 새로운 상태를 부여한다. 그리고 reward를 주는데, agent는 시간에 따라 이를 최대화할 수 있는 action을 찾는다.

Markov Property

이전 강화학습 수학에서 다루었던 개념으로 간단하게 하면 현재의 state $s_t$ 는 이전 시간 $1,2,\dots ,t$ 까지의 모든 정보를 담고 있다.

Markov Chain

이에 따라 마르코브 체인은 memoryless 한 랜덤 프로세스이다.

Markov chain은 $<\text{S, P}>$ 로 이루어진다. 기호에 대한 정의는 위에서 하였으므로 생략.(각각 Set, Transition model)

State transition matrix $P$ 는 state $s$ 에서 $s’$ 로의 확률로 이루어진 행렬로 표현할 수 있다.

$$P_{s{s}^{\prime }}=\left[\begin{array}{c}{P}_{11}\dots P_{1n}\\ ⋮\ddots ⋮\\ P_{n1}\dots P_{nn}\end{array}\right]$$

Markov chain Monte Carlo(MCMC): Gibbs Sampling

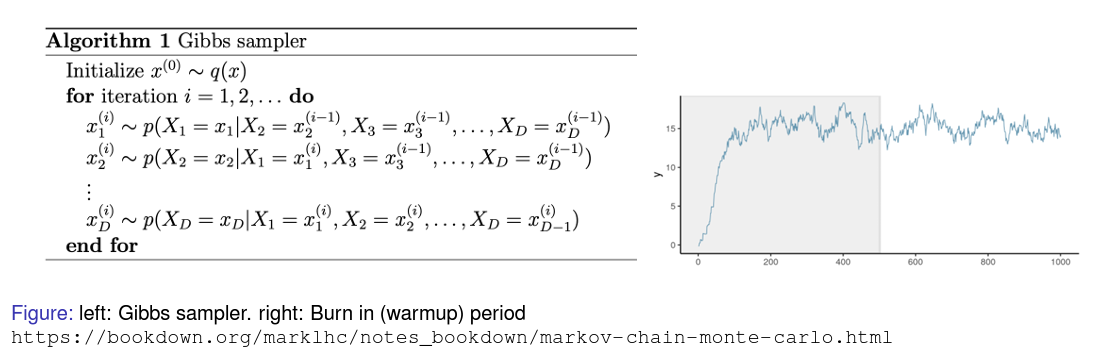
평균값으로 원하는 기댓값을 추정하기 위해 MCMC sampling이 사용될 수 있다.

Gibbs sampling은 각 변수를 조건부 분포를 이용해 샘플링하고 현재 값에 대한 변수는 고정하여 posterior sample을 생성한다. 그리고 이를 반복하여 원하는 기댓값을 추정한다.

Markov Reward Process

$<S,P,R,\gamma >$ 앞선 Markov chain에 reward 함수와 discount factor가 더해졌다. 각 notation에 대한 설명은 생략.

$G_t$ 는 현재 time step $t$ 에서의 total discounted reward이다.

$$G_t=\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k+1}$$

discount factor $\gamma$ 가 0에 가까울 수록 myopic하고, 1에 가까울 수록 far-sighted 하다. 즉, 0에 가까울 수록 현재에 가까운 값들을 더 중요하게 보고 1에 가까울 수록 멀리 본다.

대부분의 Markov reward와 decision process들을 discount한다.

이유는

• 수학적으로 편하다
• 미래에 대한 불확실성이 확실하지 않다(not fully represented)
• 경제적 관점에서는 즉각적인 reward가 더 많은 이익을 가져올 수 있다.
• 동물/인간적 행동에서는 즉각적인 보상에 더 선호를 보인다.

Bellman Equation in Matrix form

Bellman equation $V=R+\gamma PV$ 를 행렬 형태로 나타내면 아래와 같다.

가치함수 $V$ 는 행벡터가 된다.

$$\left[\begin{array}{c}V(1)\\ ⋮\\ V(n)\end{array}\right]=\left[\begin{array}{c}{R}_1\\ ⋮\\ R_n\end{array}\right]+\gamma \left[\begin{array}{c}{P}_{11}\dots P_{1n}\\ ⋮\ddots ⋮\\ P_{n1}\dots P_{nn}\end{array}\right]\left[\begin{array}{c}V(1)\\ ⋮\\ V(n)\end{array}\right]$$

Bellman equation은 선형 방정식이므로 바로 풀 수 있다.

$$\begin{array}{rl}V& =R+\gamma PV\\ V& =(1-\gamma P{)}^{-1}R\end{array}$$

이러한 역행렬을 통한 풀이의 복잡도는 $O(|S{|}^3)$ 이다. 매우 높은 계산복잡도를 가지므로 작은 Markov Reward Process에서만 바로 풀 수 있으며 큰 MRP에 대해서는 iterative methods를 사용한다.

• Dynamic programming
• Monte-Carlo evaluation
• Temporal-Difference learning

Markov Decision Process

MRP와 달리 MDP는 action과 decision-making을 포함한다.

MRP에서는 action이 없이 확률에 의해 state간의 transitions이 이루어진다.

MDP는 선택한 action과 그에 따른 transition으로 이동한다.

Policies

policy $\pi$ 는 주어진 state $s$ 에서의 action $a$ 의 분포를 의미한다.

$$\pi (a|s)=p[a_t=a|s_t=s]$$

Policy는 현재의 state에 의존하기 때문에 지난 history와는 관련이 없으므로 stationary 또는 time-independent하다고 한다.

주어진 policy에 대해서 MDP의 state sequence는 Markov chain과 같으며, state and reward sequence는 Markov Reward Process와 같다.

$$\begin{gathered} P_{s{s}^{\prime }}^{\pi }=\sum _{a\in A}\pi (a|s)P_{s{s}^{\prime }}^a \\ {R}_s^{\pi }=\sum _{a\in A}\pi (a|s)R_s^a \end{gathered}$$

Optimal Value Function

위에서 다른 state-value function과 action-value function의 최적값의 정의는 아래와 같다.

$$\begin{gathered} V^{\ast }(s)=\underset{\pi }{\max }{V}^{\pi }(s) \\ {Q}^{\ast }(s,a)=\underset{\pi }{\max }{Q}^{\pi }(s,a) \end{gathered}$$

어떤 Markov decision process 에서는 모든 optimal policies ${\pi }^{\ast }$ 에 대해 optimal value function $V^{\ast }(s)$ 와 $Q^{\ast }(s,a)$ 를 얻을 수 있다.

optimal policy는 $Q^{\ast }(s,a)$ 를 최대화함으로써 찾을 수 있다. 따라서 MDP를 푼다는 것은 $Q^{\ast }$ 를 찾는 것과 같다.

Bellman optimality equation은 nonlinear하므로 iterative methods를 통해 풀 수 있으며, value iteration, policy iteration 그리고 Q-learning 등과 같은 방법을 주로 사용한다.

Dynamic Programming

복잡한 문제를 풀기 위해 여러 작은 subproblem 들로 나누어 푸는 방식이다.

DP의 필요 조건들은 아래와 같다.

1. Optimal substructure

   Principle of optimality가 적용되며, Optimal solution은 subproblem들로 나뉘어질 수 있다.

2. Overlapping subproblems

   Subproblem들이 여러 번 발생하고, solution들을 기억해서 다시 사용할 수 있다.

MDP는 이러한 조건들을 만족한다.

• Bellman equation은 연쇄적으로 구성되어 있다.
• Value function을 가지고 다시 사용할 수 있다.

DP는 MDP에 대해 모든 것을 알고 있는 것을 전제로 한다.(Assumes full knowledge of the MDP)

For prediction

• Input: $<S,A,P,R,\gamma >$ 와 policy $\pi$
• Output: Value function $V^{\pi }$

For control

• Input: $<S,A,P,R,\gamma >$
• Output: Optimal value function $V^{\ast }$ 와 optimal policy ${\pi }^{\ast }$

Policy Evaluation

Problem: 주어진 policy $\pi$ 에 대해 value function을 평가하기

Solution 1: Bellman expectation equation을 이용한다. $V^{\pi }=(I-\gamma P^{\pi }{)}^{-1}{R}^{\pi }$

Solution 2: Iterative application $V_1\to V_2\to V_{\pi }$

각 $k+1$ 에서의 iteration에서 모든 state $s$ 에 대해 $V_k(s’)$ 를 이용해 $V_{k+1}(s)$ 를 업데이트 한다.

$$\begin{gathered} V_{k+1}(s)=\sum _{a\in A}\pi (a|s)(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{V}^{\pi }(s^{\prime }) \\ {V}^{k+1}=R^{\pi }+\gamma P^{\pi }{V}^k \end{gathered}$$

Matrix Induced Norms

행렬 $A=[a_{ij}]\in R^{m\times n}$ 로 정의되었을 때, p-norm로 유도되는 matrix norm은 아래와 같이 정의된다. (sup는 supremum 을 의미한다. i.e. the largest)

$$\Vert A{\Vert }_p=\underset{x\ne 0}{\sup }\frac{\Vert Ax{\Vert }_p}{\Vert x{\Vert }_p}=\underset{\Vert x{\Vert }_p=1}{\max }\Vert Ax{\Vert }_p$$

이에 대한 증명은 생략. $\text{if}x\ne 0,\Vert Px{\Vert }_p\le {\sup }_{x\ne 0}(\frac{\Vert Px{\Vert }_p}{\Vert x{\Vert }_p})\Vert x{\Vert }_p$ 를 이용.

Contraction Mapping Theorem

Definition

Let (X, d) be a complete metric space. Then a map T: X→X is called a contraction mapping on X if there exists $q\in [0,1)$ such that

$$d(T(x)T(y))\le qd(x,y),\forall x,y\in X$$

Theorem

Let (X, d) be a non-empty complete metric space with a contraction mapping T: X→X. Then T admits a unique fixed-point $x^{\ast }\in X$ i.e. $T(x^{\ast })=x^{\ast }$.

Furthermore, $x^{\ast }$ can be found as follows: start with an arbitrary element $x_0\in X$ and define a sequence $x_n$ by $x_n=T(x_{n-1})$ for $n\ge 1$ . Then $x_n\to x^{\ast }$

결론적으로, 특정 조건 하에서 반복적으로 mapping이 이루어지면 결국 한 지점으로 수렴한다는 것을 의미한다.

Convergence of Value Iteration

Theorem

Value iteration은 optimal value로 수렴한다 $\hat{V}\to V^{\ast }$

Proof.

어떤 Value function $\hat{V}$ 에 대한 추정으로 Bellman backup operator $B:{\mathbb{R}}^{|S|}\to {\mathbb{R}}^{|S|}$ 을 정의한다.

$$B(\hat{V})=\underset{\pi }{\max }(R^{\pi }+\gamma P^{\pi }\hat{V})$$

그리고 $B$ 가 $\gamma$ -contraction이라는 것을 보이자.

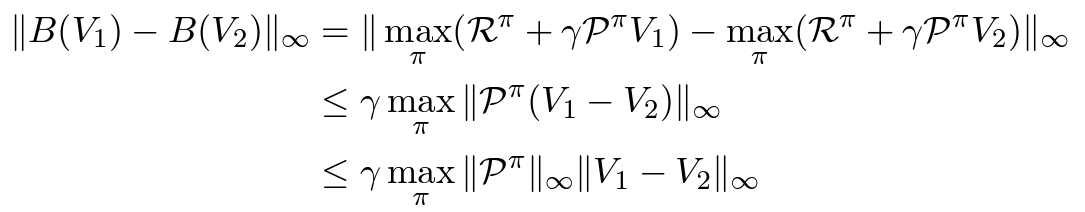
$\Vert P^{\pi }{\Vert }_{\infty }={\max }_{s\in S}{\sum }_{s’\in S}{P}_{ss’}=1$ 이고, ${\max }_{\pi }\Vert V_1-V_2{\Vert }_{\infty }=\Vert V_1-V_2{\Vert }_{\infty }$ 이므로 결국 아래와 같이 정리된다.

$$\Vert B(V_1)-B(V{)}_2{\Vert }_{\infty }\le \gamma \Vert V_1-V_2{\Vert }_{\infty }$$

the contraction mapping theorem에 의해 우리는 Optimal value function을 찾을 수 있다.

Policy Iteration

1. 무작위 policy $\hat{\pi }$ 로 초기값을 설정한다.
2. Policy evalution: policy의 가치 $V^{\pi }$ 를 계산한다. 선형 방정식을 풀거나 iterative method 사용
3. Policy improvement: $V^{\pi }$ 를 이용해 $\pi$ 를 업데이트 한다.
4. 만약 $\pi$ 가 변한다면 step 2로 돌아가 반복한다.

Generalized Policy Iteration

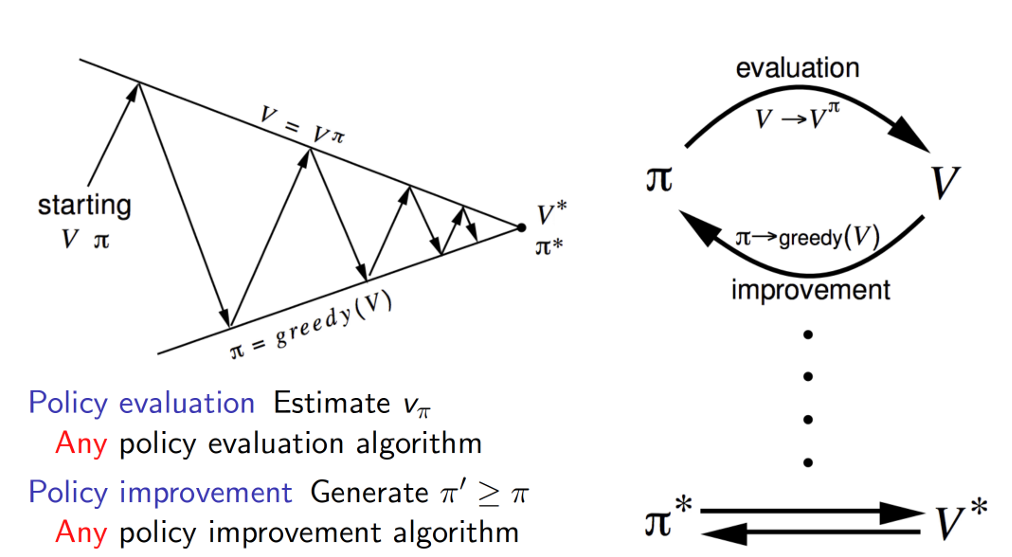
Value Iteration vs Policy Iteration

finite-time convergence 때문에 보통 Policy iteration이 이상적이다.

그러나 선형 방정식을 푸는 것은 계산 복잡도가 크다.

Value iteration은 매 iteration마다 $O(|S|\times |A|)$ 의 시간을 필요로 한다.

보통 policy iteration이 빠르게 수렴한다.