[T-RO '22] Model Predictive Contouring Control for Time-Optimal Quadrotor Flight

Model Predictive Contouring Control for Time-Optimal Quadrotor Flight

IEEE

Cite

A. Romero, S. Sun, P. Foehn and D. Scaramuzza, "Model Predictive Contouring Control for Time-Optimal Quadrotor Flight," in _IEEE Transactions on Robotics_, vol. 38, no. 6, pp. 3340-3356, Dec. 2022, doi: 10.1109/TRO.2022.3173711

이 논문은 Scaramuzza 교수님 연구실에서 publish 된 quadrotor 에서의 Model Predictive Contouring Control (MPCC) 방법론에 대한 논문이다.

전통적인 방식은 trajectory planning과 tracking을 별도로 처리하기 때문에 time-optimal 한 trajectory 를 필요로 한다. 그러나 본 논문은 MPCC 를 통해 reference path 를 tracking 하면서 동시에 time allocation 을 처리한다.

Introduction

Quadrotor 드론에서의 time-optimal flight는 복잡한 nonlinear dynamics, aerodynamics 및 actuator constraints 등으로 인해 실시간 구현에 어려움이 있다. 기존 방법은 trajectory planning 과 tracking 을 나누어 수행하며, 이로 인해 실시간 재계획이 어렵다는 문제점이 존재했다.

Time-optimal multiwaypoint flight

[1] P. Foehn, A. Romero, and D. Scaramuzza, “Time-optimal planning for quadrotor waypoint flight,” Sci. Robot., vol. 6, no. 56, 2021, Art. no. eabh1221.
[2] G. Ryou, E. Tal, and S. Karaman, “Multi-fidelity black-box optimization for time-optimal quadrotor maneuvers,” Int. J. Robot. Res., 2020, Art. no. 02783649211033317.

그렇기 때문에 보수적인 actuation limit 을 가지거나 미리 생성된 궤적에서 약간만 벗어나도 (외란이나 model mismatch 등으로 인해) online 으로 경로 재생성이 필요한데, 현재 solver 성능으로는 제약이 있다. 그래서 computationally efficient 한 접근으로는 point mass 로 기체를 모델링 하거나 polynomial 로 궤적을 근사하는 것이다.

For point-mass model (PMM) approaches, the problem of finding time-optimal point-to-point trajectories has a closed-form solution [19] and is, therefore, very fast to solve. However, these simplified trajectories lack the notion of 3D rotation and are dynamically infeasible (since quadrotors are underactuated systems, they need to rotate to align their thrust with the desired acceleration direction). On the other hand, polynomial trajectories offer a fast way of generating feasible paths. However, polynomial control inputs are smooth and cannot fully exploit the actuator potential, rendering control policies suboptimal.

III. Methodology

Model Predictive Contouring Control

MPCC는 trajectory의 거리를 최소화하면서도 주어진 경로를 따라 최대한 빠르게 이동하는 것을 목표로 한다.

추종해야 하는 reference path 의 arc length (혹은 progress) 를 $\theta$ 로 하고 $k$ 시점의 현재 arc length 를 ${\theta }_k$ 라고 하자. 그렇다면 $\theta$ 로 parameterize 한 3차원 path 를 ${\mathbf{p}}^d(\theta )=[x^d(\theta )y^d(\theta )z^d(\theta ){]}^T$ 로 표현할 수 있고, $k$ 시점의 드론 위치를 ${\mathbf{p}}_k=[x_k{y}_k{z}_k{]}^T$ 로 둔다.

Model predictive contouring control

D. Lam, C. Manzie, and M. Good, “Model predictive contouring control,” in Proc. 49th IEEE Conf. Decis. Control, 2010, pp. 6137–6142.

$$J_{\text{MPCC}}(\mathbf{x})=\sum _{k=0}^N{q}_c(e_k^c{)}^2-\rho {\theta }_N$$

MPCC 수식은 ${\mathbf{p}}_k$ 와 ${\mathbf{p}}^d(\theta )$ 간의 projected distance 를 최소화하면서 progress $\theta$ 를 최대화 하는 cost function 으로 구성된다. 위 수식에서 $e_k^c$ 는 $k$ step 에서의 contour error 로 그림의 초록색 선에 해당한다.

$$e_k^c=\underset{\theta }{\min }\Vert {\mathbf{p}}_k-{\mathbf{p}}^d(\theta ){\Vert }_2$$

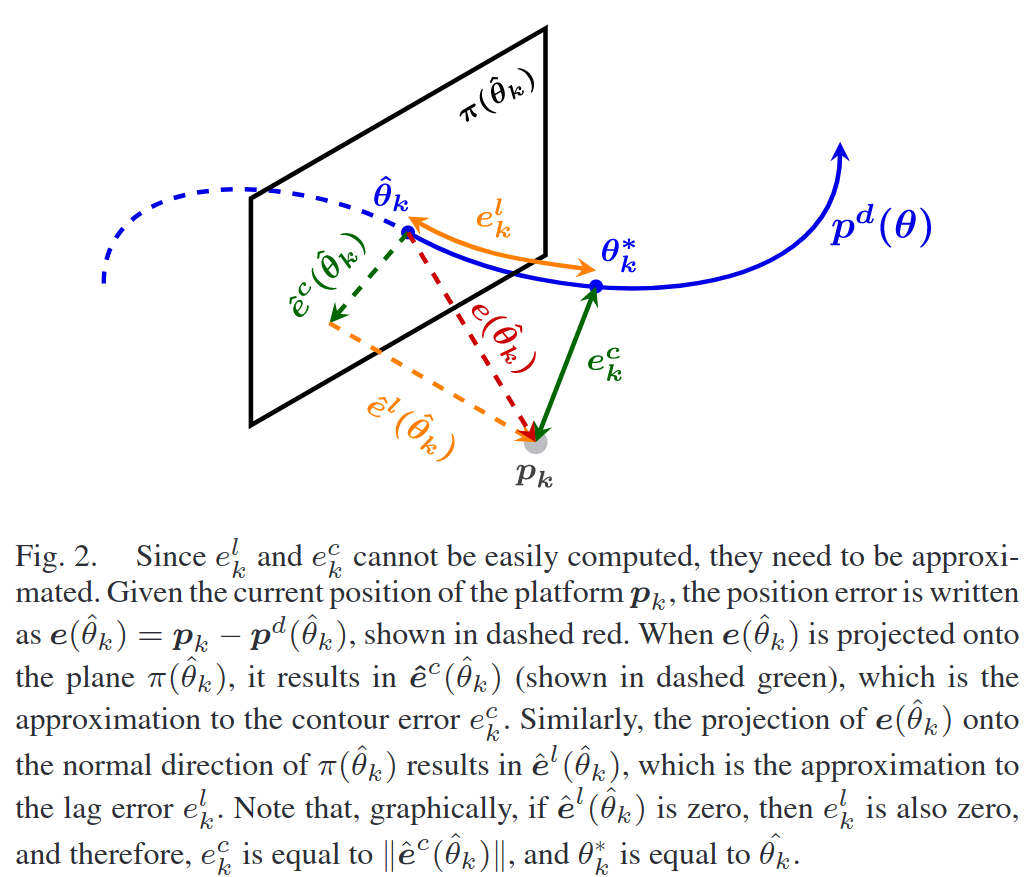
여기서 $e_k^c$ 를 구하는 것 또한 또다른 최적화문제이기 때문에, MPCC 의 본 cost function 을 online 으로 푸는데에 어려움이 있다. 이를 해결하기 위해 본 논문에서는 ${\hat{\theta }}_k$ 를 도입하여 ${\theta }_k^{\ast }$ 를 근사하고자 한다.

$${\hat{\theta }}_{k+1}={\hat{\theta }}_k+v_{\hat{\theta }}\Delta t$$

여기서 v_\hat{\theta}=\frac{\Delta \hat{\theta}_k}{\Delta t} 로 virtual control 로 추후에 MPCC 를 풀어 얻은 output 이 된다.

그리서 위 그림의 초록색 점선에 해당하는 ${\hat{e}}^c({\hat{\theta }}_k)$ 로 근사하게 되고, 이를 정확하게 근사하기 위해서는 lag error 의 근사인 ${\hat{e}}^l({\hat{\theta }}_k)$ 가 최소화가 되어야 한다.

이를 고려한 최종적인 MPCC 수식은 아래와 같다.

$$\begin{array}{rl}\pi (\mathbf{x})={\arg \min }_u& \sum _{k=0}^N\Vert {\hat{e}}^c({\hat{\theta }}_k){\Vert }_{q_c}^2+\Vert {\hat{e}}^l({\hat{\theta }}_k){\Vert }_{q_l}^2-\mu v_{\hat{\theta },k}\\ \text{subject to}& {\mathbf{x}}_0=\mathbf{x}\\ & {\mathbf{x}}_{k+1}=f(x_k,u_k)\\ & {\mathbf{x}}_k\in \mathcal{X}{\mathbf{u}}_k\in \mathcal{U}\end{array}$$

이 때 quadratic term 에 들어간 $q_c,q_l$ 은 weight term 이라고 한다. 인용된 MPCC 본 논문과 같이 정확한 approximation 을 위해 $q_l$ 은 높게 골라진다고 한다.

Arc-Length Parameterization of the Paths

일반적인 곡선의 arc-length parameterization 을 구하는 것은 불가능에 가까우므로 본 논문은 근사화를 제안한다.

주어진 3차원 경로 ${\mathbf{p}}^d(t)$ 가 연속적인 궤적으로 주어진다면, bisection method 를 통해 여러 sample 들 간의 arc length 가 동일하도록 나누고 이를 binary search 를 하여 $\theta$ 를 찾는 것이다.

만약 경로점 처럼 연속적인 점들로 주어진다면 각 점들간의 선형성을 가정하여 equidistance 한 segment 를 탐색한다. 두 가지 경우 모두 각 점들에 대응되는 arc length, position, normalized velocity 를 저장한다.

이를 통해 3차원 스플라인 ${\mathbf{\rho }}_i({\theta }_k)i\in [-,\dots ,P-1]$ 을 아래와 같이 얻을 수 있다.

$${\mathbf{p}}^d({\theta }_k)=\{\begin{array}{ll}{\mathbf{\rho }}_0({\theta }_k)& 0\le {\theta }_k\le {\theta }_0\\ {\mathbf{\rho }}_1({\theta }_k)& {\theta }_1\le {\theta }_k\le {\theta }_2\\ ⋮{\mathbf{\rho }}_{\mathbf{P}-1}({\theta }_k)& {\theta }_{P-1}\le {\theta }_k\le {\theta }_P\end{array}$$

Derivation of Contour and Lag Errors in 3D

${\mathbf{p}}^d({\theta }_k)$ 의 tangent line 을 $\mathbf{t}({\theta }_k)\in {\mathbb{R}}^3$ 로 정의하자. 그러면 아래와 같은 관계를 유도할 수 있다.

$$\begin{array}{rl}{\theta }_k& ={\int }_0^{{\theta }_k}\Vert ({\mathbf{p}}^d{)}^{\prime }(t)\Vert dt⟺\\ \frac{d{\theta }_k}{d{\theta }_k}& =\frac{d{\int }_0^{{\theta }_k}\Vert ({\mathbf{p}}^d{)}^{\prime }(t)\Vert dt}{d{\theta }_k}⟺\\ 1& =\Vert ({\mathbf{p}}^d{)}^{\prime }(t)\Vert =\Vert \frac{d{\mathbf{p}}^d({\theta }_k)}{d{\theta }_k}\Vert =\Vert \mathbf{t}({\theta }_k)\Vert \end{array}\text{\hspace{1em}(9)}$$

앞서 그림에서 보았듯이, $\mathbf{e}({\theta }_k)$ 는 tangent line $\mathbf{t}({\theta }_k)$ 에 사영(projection) 된 ${\mathbf{e}}^l({\theta }_k)$ 와 평면 $\pi ({\theta }_k)$ 에 있는 ${\mathbf{e}}^c({\theta }_k)$ 로 구성하여 $\mathbf{e}({\theta }_k)={\mathbf{e}}^l({\theta }_k)+{\mathbf{e}}^c({\theta }_k)$ 로 표현할 수 있다. ($\widehat{(\cdot )}$ 은 모두 생략)

$\mathbf{t}({\theta }_k)$ 로 사영된 $\mathbf{e}({\theta }_k)$ 인 ${\mathbf{e}}^l({\theta }_k)$ 는 아래와 같고,

$${\mathbf{e}}^l({\theta }_k)=(\mathbf{t}({\theta }_k{)}^T\cdot \mathbf{e}({\theta }_k))\mathbf{t}({\theta }_k)=e^l({\theta }_k)\mathbf{t}({\theta }_k)$$

우리가 최소화하려는 $q_l$-weighted norm 을 수식 (9)를 이용해 아래와 같이 정리할 수 있다.

$$\Vert e_l({\theta }_k){\Vert }_{q_l}^2=\Vert e_l({\theta }_k){\Vert }_{q_l}^2\cdot \Vert t({\theta }_k){\Vert }_{q_l}^2=q_l\cdot e_l({\theta }_k{)}^2\text{\hspace{1em}(10)}$$

이와 같이 $e_c({\theta }_k)$ 를 구하면 아래와 같이 표현할 수 있다.

$$e_c({\theta }_k)=e({\theta }_k)-e_l({\theta }_k)=\left[\begin{array}{ccc}1-t_x^2({\theta }_k)& -t_x({\theta }_k)t_y({\theta }_k)& -t_x({\theta }_k)t_z({\theta }_k)\\ -t_x({\theta }_k)t_y({\theta }_k)& 1-t_y^2({\theta }_k)& -t_y({\theta }_k)t_z({\theta }_k)\\ -t_x({\theta }_k)t_z({\theta }_k)& -t_y({\theta }_k)t_z({\theta }_k)& 1-t_z^2({\theta }_k)\end{array}\right]e({\theta }_k)$$

마찬가지로 $q_c$-weighted norm 은 아래와 같다.

$$\Vert e_c({\theta }_k){\Vert }_{q_c}^2=e_c({\theta }_k{)}^{\top }{Q}_c{e}_c({\theta }_k)\text{\hspace{1em}(11)}$$

IV. Application to Quadrotors

Quadrotor Dynamics

$$\begin{array}{rl}\dot{p}& =v\\ \dot{q}& =\frac{1}{2}q\otimes \left[\begin{array}{c}0\\ \omega \end{array}\right]\\ \dot{v}& =g+\frac{1}{m}R(q)f_T\\ \dot{\omega }& =J^{-1}\left(\tau -\omega \times J\omega \right)\end{array}\text{\hspace{1em}(12)}$$ $$f_T=\left[\begin{array}{c}0\\ 0\\ \sum f_i\end{array}\right],\tau =\left[\begin{array}{c}\frac{l}{\sqrt{2}}(f_1+f_2-f_3-f_4)\\ \frac{l}{\sqrt{2}}(-f_1+f_2+f_3-f_4)\\ c_{\tau }(f_1-f_2+f_3-f_4)\end{array}\right]\text{\hspace{1em}(13)}$$

위 Dynamics 수식 자세한 내용은 생략, 본 논문에서는 aerodynamic effects 를 고려한 linear drag model 을 사용해서 아래와 같이 expand 하여 사용했다. 여기서 $\mathbf{D}=\text{diag}(d_x,d_y,d_z)$ 이다.

$$\dot{v}=g+\frac{1}{m}R(q)f_T-R(q)D{R}^{\top }(q)v\text{\hspace{1em}(14)}$$

Optimal Control Problem Formulation

앞서 소개된 dynamics 를 MPCC 수식에서 고려하기 위해 아래와 같이 state, control space 를 정의한다.

하지만 virtual input 으로 사용된 $v_{\theta }$ 의 변화를 제한하기 위해 progress acceleration $\Delta v_{\theta }=\frac{d{v}_{\theta }}{dt}$ 를 도입하였다.

$$x=\left[\begin{array}{c}p\\ q\\ v\\ \omega \\ f\\ \theta \\ v_{\theta }\end{array}\right],u=\left[\begin{array}{c}\Delta v_{\theta }\\ \Delta f\end{array}\right]\text{\hspace{1em}(15)}$$

augmented 된 state 들은 아래와 같이 선형 dynamics 를 사용한다.

$$\begin{array}{rl}{f}_{k+1}& =f_k+\Delta f_k\Delta t\\ {\theta }_{k+1}& ={\theta }_k+v_{\theta ,k}\Delta t\\ v_{\theta ,k+1}& =v_{\theta ,k}+\Delta v_{\theta ,k}\Delta t\end{array}\text{\hspace{1em}(16)}$$

그러면 최종적인 OCP(Optimal Control Problem) 은 아래와 같다.

$$\begin{array}{rl}\pi (x)=\arg \underset{u}{\min }& \sum _{k=0}^N(\Vert e_l({\theta }_k){\Vert }_{q_l}^2+\Vert e_c({\theta }_k){\Vert }_{q_c}^2+\Vert {\omega }_k{\Vert }_{Q_{\omega }}^2\\ & +\Vert \Delta v_{\theta ,k}{\Vert }_{r_{\Delta v}}^2+\Vert \Delta f_k{\Vert }_{R_{\Delta f}}^2-\mu v_{\theta ,k})\\ \text{subject to:}& x_0=x\\ & x_{k+1}=f(x_k,u_k)\\ & {\omega }_{\min }\le {\omega }_k\le {\omega }_{\max }\\ & f_{\min }\le f_k\le f_{\max }\\ & 0\le v_{\theta ,k}\le v_{\theta ,\max }\\ & \Delta v_{\theta ,\min }\le \Delta v_{\theta ,k}\le \Delta v_{\theta ,\max }\\ & \Delta f_{\min }\le \Delta f_k\le \Delta f_{\max }\end{array}\text{\hspace{1em}(17)}$$

기존 OCP 수식에서 몇 가지 더해진 term 과 contraint 가 있는데 이들은 안정적인 application 을 위함이라고 한다. 예를 들어, virtual input $\Delta v_{\theta }$ 와 $\Delta f$, 그리고 $\mathbf{w}$ 이 그렇다. ($\mathbf{w}$ 은 body rates 를 낮게 유지하게 하여 안정적이게 하는데 중요하다고 함.) 그래서 $\min ,\max$ term 들은 모두 tuning parameter 에 해당한다.

지금까지의 설명을 포함하여 전체 알고리즘은 아래와 같다.

Dynamic Allocation of Contouring Weight

MPCC 는 reference path 를 정교하게 따라가기 보다 빠르게 따라가는 성향이 있는데 이는 progress weight 혹은 controuring error weight term 에 따라 달라진다.

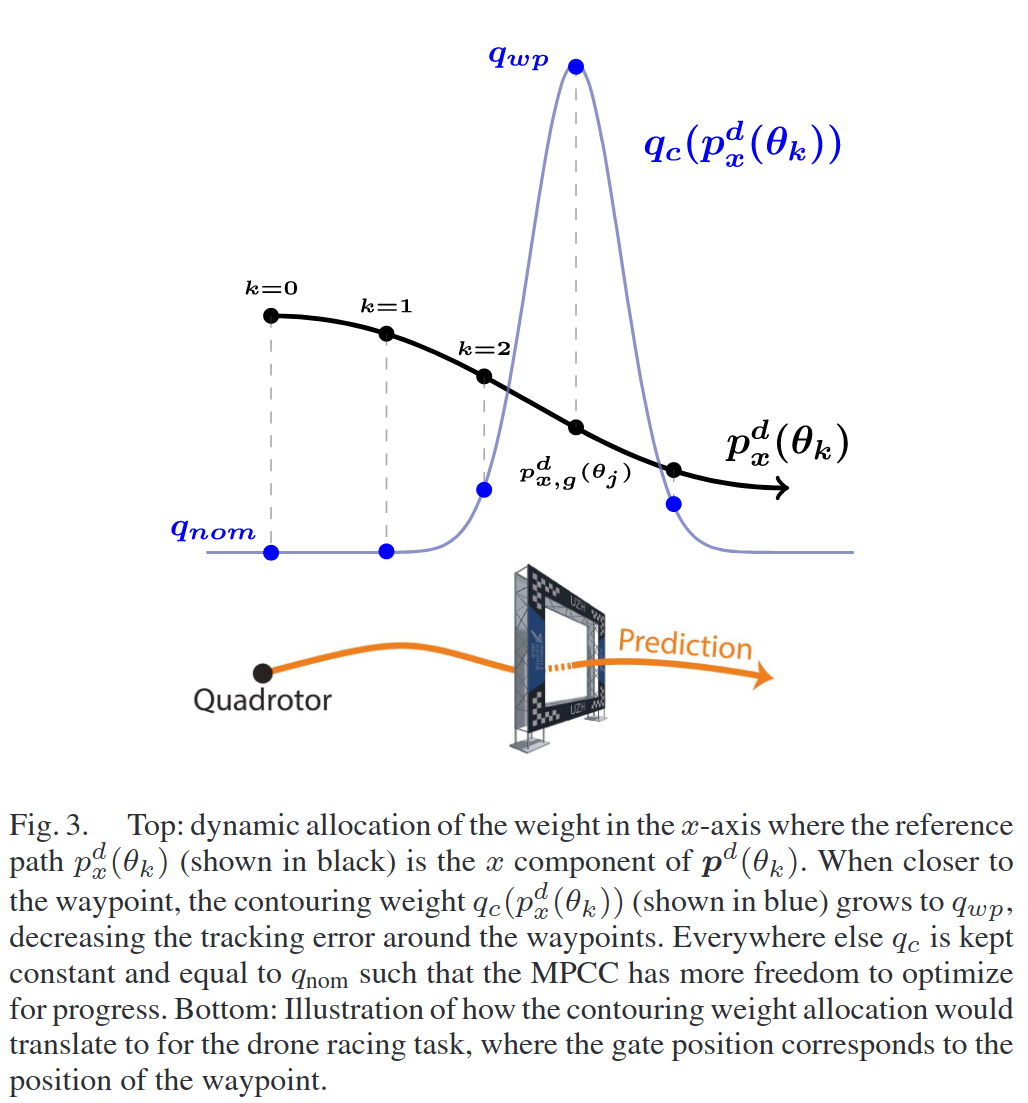
위 그림처럼 레이싱 같은 환경에서는 꼭 지나가야 하는 gate 에서는 progress 를 우선시하기보다 contour error 를 최대한 줄여야 한다.

그래서 본 논문에서는 이를 동적으로 할당한다. 자세한 사항은 직접 논문 참고.

Path Generation

이 섹션에서는 MPCC 에서 사용할 ${\mathbf{p}}^d(t)$ 를 생성하는 3가지 방식에 대해 소개한다.

Multiwaypoint Minimum Snap

드론 분야에서는 minimum snap trajectory 가 널리 사용되고 있다. 드론의 differential flatness 한 특성 덕분에 full state trajectory representation 으로 적합하기 때문이다. 하지만 단점은 control input 이 polynomial 의 미분으로만 구성될 수 있다는 점이다.

Polynomial 은 smooth 하고 한 점에서 가장 좋은 값만 갖기 때문에 갑자기 빠르게 변하는 control input 을 갖기 어렵다. 본 논문에서는 receding horizon 방식으로 polynomial 을 생성하였고, $N$ 개의 다음 waypoint 를 가지며 snap 을 최소화하도록 생성하였다.

그리고 다음 waypoint 로 이동한 후에는 자동으로 replanning 하도록 하였다. 이렇게 함으로써 한번에 모든 gate 를 지남으로 인해 numerical issue 를 발생시키지 않고자 하였다고 한다.

Time-Optimal Full Model

![cite] CPC

P. Foehn, A. Romero, and D. Scaramuzza, “Time-optimal planning for quadrotor waypoint flight,” Sci. Robot., vol. 6, no. 56, 2021, Art. no. eabh1221.

여기서는 CPC 를 기반으로 하여 full nonlinear model 을 고려하는 궤적을 만들었다. 이는 state-of-the-art time-optimal 한 플래닝 방식이다.

언급한 단점으로는, 궤적 자체는 discretized 되어 있고 platform 의 model 이 정확하긴 하더라도 완벽하진 않다는 것이다.

또한, 몇 시간에 걸친 offline 방식으로 생성되기 때문에 real-time 으로 재생성 하는 것은 불가능하다.

Time-Optimal PMM

MPCC 의 장점 중 하나로 infieasible 한 경로여도 MPCC 에서 자체적으로 time allocation 을 하면서 따라가기 때문에 큰 문제가 되지 않는다.

그렇기 때문에 단순한 PMM 으로 모델링하여 궤적을 만들었을 때의 MPCC 성능을 보고자 하였다.

Point mass 를 사용하기 때문에 연산적으로 매우 우수하고 closed-form 으로 해를 얻을 수 있다.

본 논문에서는 아래 논문에서 사용된 방식을 차용하였다고 한다.

PMM

P. Foehn et al., “AlphaPilot: Autonomous drone racing,” Auton. Robots, vol. 46, no. 1, pp. 307–320, 2022.

PMM 에서는 $\ddot{p}=u$ 로 모델링하고 Pontryagin’s maxium principle 을 이용해 acceleration 과 velocity 에 대한 bound constraint 를 부여하여 bang-singular-bang solution 을 사용하였다고 한다. 자세한 내용은 본 논문과 2024-09-08-BangBangControl 을 참고해보자.

Experiments & Results

Simulation

• 기준 궤적에 따른 성능 차이 (Ablation Study):

  • MPCC는 기준 궤적의 품질에 따라 결과 성능 차이가 있음.

  • Minimum snap trajectory는 계산은 빠르지만 최적성 낮음.

  • CPC trajectory는 시간 최적성이 높으나 오프라인 계산에 수 분~수 시간이 걸림.

  • PMM (point-mass model) 기반 경로는 계산이 빠르며, MPCC와 결합 시 CPC 수준에 가까운 성능 발휘.

• 딜레이 견딤 성능 (Time Delay Study):

  • 위치/자세 측정 지연을 0~60ms까지 시뮬레이션.

  • MPCC는 최대 50ms까지 안정적으로 주행 가능, 반면 MPC는 25ms부터 실패.

Conclusion

• MPCC는 시간 최적 드론 주행을 실시간으로 가능하게 한다:

  • 기존 오프라인 최적화 방식 (예: CPC) 대비 계산 부담이 낮고, 동적 상황에 대응 가능.

• PMM과의 결합으로 실시간 경로 생성 + 제어 가능:

  • 기준 경로가 물리적으로 정확하지 않아도 MPCC가 이를 효과적으로 따라감.
  • 고속 + 안정성 + 계산 효율 모두 확보.

• 실세계 실험을 통해 성능 검증 완료:

  • 드론 레이싱 트랙에서 세계 수준 조종사를 이김.
  • 실시간 재계획, 센서 딜레이, 제약 고려 등 실제 환경 요소를 통합해 안정적 비행 달성.