[CS285] 9. Advanced Policy Gradients

Lecture 9: Advanced Policy Gradients

Part 1

이전에 배운 policy gradients 알고리즘을 생각해보자.

1. Generate samples $\{{\tau }^i\}$
2. Fit a model to estimate return ${\hat{Q}}^{\pi }(x_t,u_t)={\sum }_{t^{\prime }=t}^{T}r(x_{t^{\prime }},u_{t^{\prime }})$
3. Improve the policy $\theta \leftarrow \theta +\alpha {\nabla }_{\theta }J(\theta )$

Gradient descent 를 이용해 policy 를 개선하는 방식은 지난 주차 내용 의 value-based method 중 policy iteration algorithm 과 닮아있다.

차이점은 policy iteration 은 policy 를 update 할 때 $\arg \max$ 를 사용했다는 점이다. Policy gradient 는 한번에 점프하는 대신 개선이 더 많은 방향으로 점진적으로 이동한다.

Policy gradient as policy iteration

여기서 이야기하는 ${\theta }^{\prime }$ 은 updated 된 policy 의 파라미터이고, $\theta$ 는 이전의 것이다. 그래서 이 둘의 차이를 $E_{\tau \sim p_{{\theta }^{\prime }}(\tau )}[{\sum }_t{\gamma }^t{A}^{{\pi }_{\theta }}(s_t,a_t)]$ 로 설정하였다. 이 둘의 차이가 가장 크다면 우리는 policy $\pi$ 를 가장 크게 개선했다고 할 수 있을 것이다.

그리고 우리는 ${\theta }^{\prime }$ 에서의 $E[V^{{\pi }_{\theta }}]$ 를 최대화 하는 것이 올바른 방향임을 보이고자 한다.

$E_{s_0\sim p(s_0)}$ 는 policy 에 좌우되지 않으므로 이를 $E_{\tau \sim p_{{\theta }^{\prime }}(\tau )}$ 로 표현해도 변하지 않는다.

수식의 전개를 차근히 따라가보면 결국 advantage 로 수식이 표현되는 것을 알 수 있고, 둘의 차이를 claim 한 것이 옳다는 것을 증명하였다.

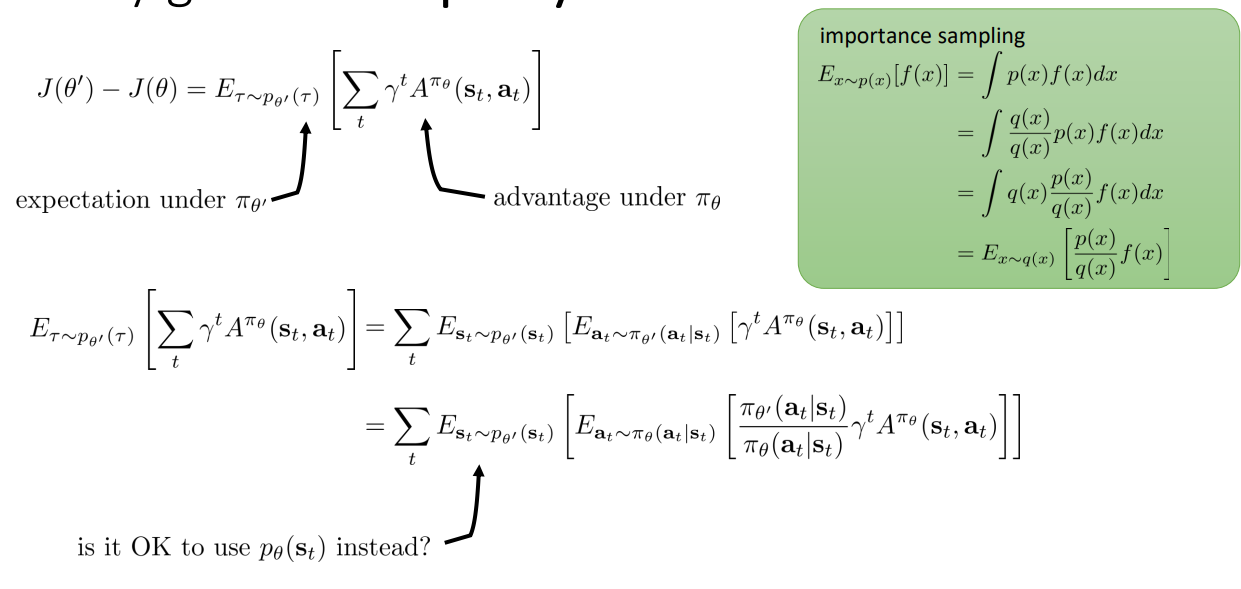
하지만 분포의 차이를 무시해도 괜찮은 것일까? 우리가 결국 하고 싶은 것은 $J({\theta }^{\prime })-J(\theta )\approx \bar{A}({\theta }^{\prime })$ 임을 보여서 improved 된 ${\pi }^{\prime }$ 를 구할 때 $\bar{A}({\theta }^{\prime })$ 를 사용하고자 하는 것이다.

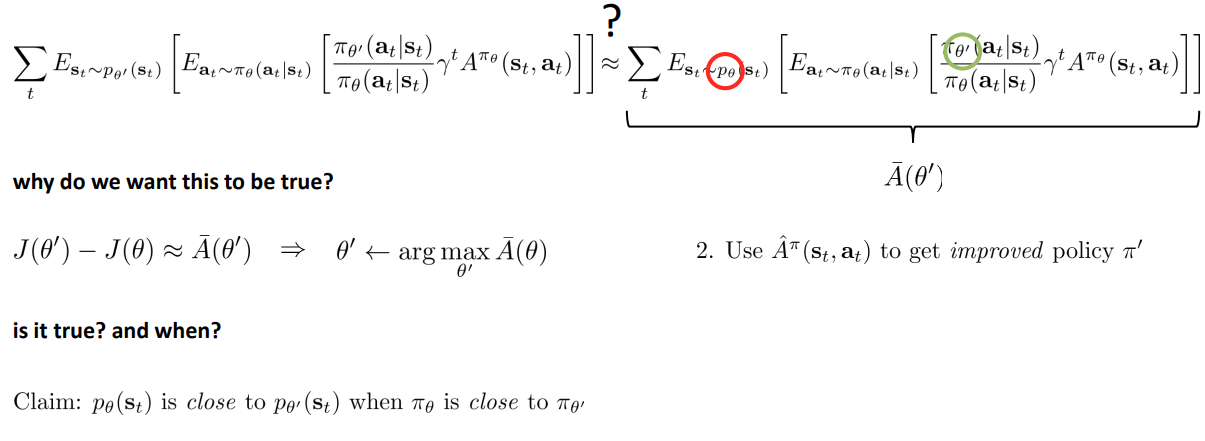
이 근사가 참인지 그리고 어떨 때 참일 수 있는지에 대해 다음 파트에서 알아보도록 한다.

Part 2: Bounding the Distribution Change

Stochastic 한 경우 이전에 deterministic 한 경우를 먼저 살펴보자.

여기서 나온 수식은 2주차 강의 에서 나온 것을 기억해내면 이해는 어렵지 않다.

이제 임의의 분포에서 어떤지 알아보자.

기댓값에 대해서도 boundary 를 둘 수 있지만 쉽게 살펴보기 위해 크기에 대한 boundary 로 설명한다고 한다.

슬라이드에 있는 lemma 를 이용하면 stochastic 한 경우에 대해서도 이전처럼 증명을 보일 수 있다.

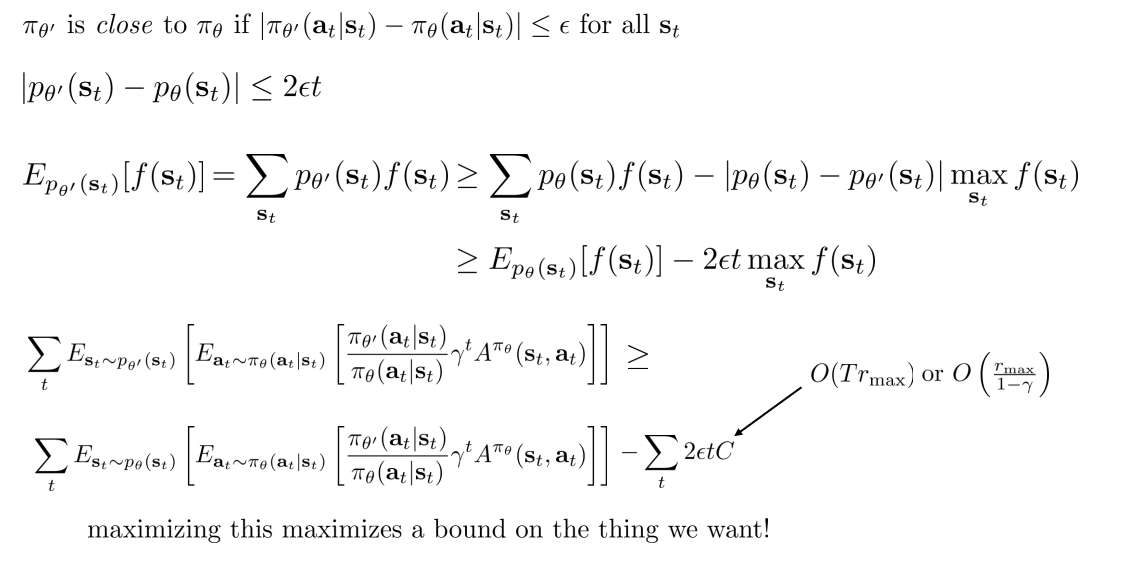
우리의 Claim 이 참인지 보기 위해 식을 정리해보면 $-{\sum }_{t}2ϵtC$ 항의 차이로 정리된다. 그렇다면 $C$ 의 값을 어떻게 사용해야 할까.

Advantage function 은 return 의 합이므로 $C$ 의 최댓값은 $T{r}_{max}$ 가 됨을 알 수 있고, 이것의 복잡도를 적절히 표현할 수 있다. Infinite 한 경우에는 $\frac{r_{max}}{1-\gamma }$ 로 표현할 수 있다.

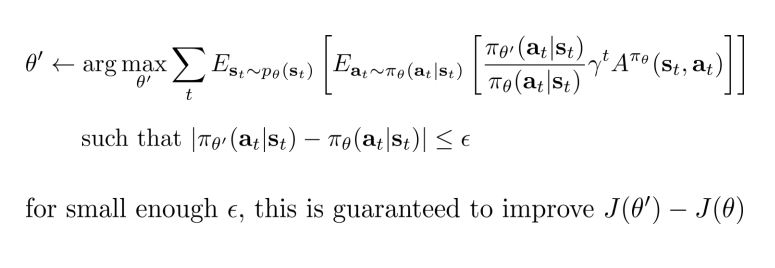
여태까지의 내용을 정리하면 gradient descent 를 수행할 때 ${\theta }^{\prime }\leftarrow \arg \max \bar{A}({\theta }^{\prime })$ 할 수 있음을 보이고자 하였고, boundary 조건에서 이를 증명하였다.

Part 3: Policy Gradients with Constraints

A more convenient bound

앞서 다룬 bound 에서 가장 편한 방식은 KL divergence 를 사용하는 것이다.

Question

• 여기에서 $\sqrt{\frac{1}{2}{D}_{KL}({\pi }_{{\theta }^{\prime }}(\cdot )\Vert {\pi }_{\theta }(\cdot ))}$ 은 어떻게 유도된 것인지?

How do we enforce the constraint?

이제 ${\theta }^{\prime }\leftarrow \arg \max \bar{A}({\theta }^{\prime })$ 로 ${\theta }^{\prime }$ 를 update 할 때 bound 를 만족해야 $\bar{A}({\theta }^{\prime })$ 를 사용하는 것이 가능하다.

그렇다면 어떻게 제약조건을 만족하도록 할 수 있을까?

가장 쉬운 방식은 라그랑지안 CO 를 사용하는 것이다. 즉, 제약조건을 직접 만족시키도록 하는 대신에 $-\lambda$ 를 곱하여 목적함수에 추가해주는 것이다.

Natural Gradient

또다른 방법 중 하나는 First-order Taylor approximation 을 사용하는 것이다. 그래서 단순하게 ${\nabla }_{\theta }\bar{A}(\theta {)}^T({\theta }^{\prime }-\theta )$ 를 계산한다. ($\bar{A}({\theta }^{\prime })$ 가 아닌 $\bar{A}(\theta )$ 임에 유의)

그리고 제한 조건을 고려하여 closed-form solution 을 도출할 수 있다고 한다.

Can we just use the gradient then?

$$\begin{array}{rl}{\theta }^{\prime }\leftarrow & \arg \underset{{\theta }^{\prime }}{\max }{\nabla }_{\theta }J(\theta {)}^T({\theta }^{\prime }-\theta )\\ & \text{such that}{D}_{KL}({\pi }_{{\theta }^{\prime }}(a_t|s_t)\Vert {\pi }_{\theta }(a_t|s_t))<ϵ\end{array}$$

우리가 풀어내는 식 대신 GD 처럼 $\theta \leftarrow \theta +\alpha {\nabla }_{\theta }J(\theta )$ 를 해볼 수 있을 것이다.

문제는, 제약조건을 만족하도록 $\theta$ 의 해당하는 parameter 를 조금만 바꾸더라도 어떤 parameter 들은 probability 를 매우 많이 바꿀 수 있다는 것이다.

따라서 gradient descent 방식으로 CO 를 해결할 수는 있지만, KL space 가 아닌 $\theta$ space 에서 제약조건을 고려하는 것이 되어 제대로 제약조건을 고려하지 않는 것이 된다.

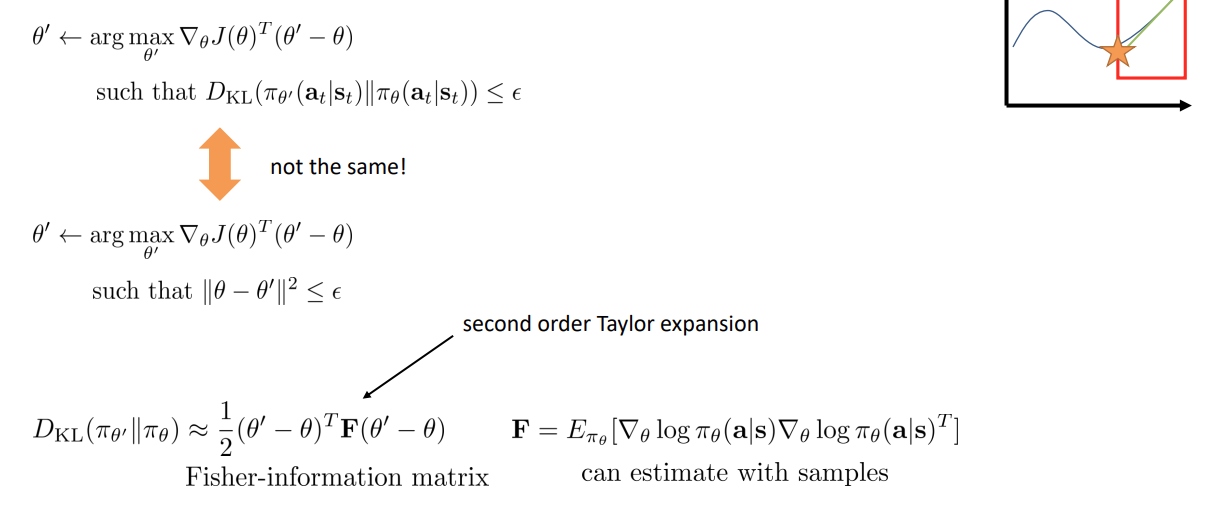
제대로 하는 방법은 $D_{KL}$ 을 2차 테일러 급수로 근사하여 하는 것으로, 이는 quadratic constraint 를 갖는 것과 유사하기도 하다. 그래서 이를 계산할 때 샘플들의 기댓값을 이용해 estimate 할 수 있다.

$D_{KL}$ 을 2차 급수로 근사하는 유도과정은 생략.

$$\begin{array}{rl}\text{Maximize}& {\nabla }_{\theta }J(\theta {)}^{\top }\Delta \theta \\ \text{s.t.}& \frac{1}{2}\Delta {\theta }^{\top }F\Delta \theta <\delta \end{array}$$

위 수식을 Langrange multiplier 를 이용하여 gradient step 을 계산하면 아래와 같다.

$$\begin{array}{rl}& \mathcal{L}={\nabla }_{\theta }J(\theta {)}^{\top }\Delta \theta -\lambda (\frac{1}{2}\Delta {\theta }^{\top }F\Delta \theta -\delta )\\ & {\nabla }_{\Delta \theta }\mathcal{L}={\nabla }_{\theta }J(\theta )-\lambda F_{\theta }\Delta \theta \\ & \\ & {\nabla }_{\Delta \theta }\mathcal{L}=0,\Delta \theta =\frac{1}{\lambda }{F}_{\theta }^{-1}{\nabla }_{\theta }J(\theta )\end{array}$$

얻어진 step 을 constraint 에 다시 넣으면 $\lambda$ 를 구할 수 있다.

$$\begin{array}{rl}& \frac{1}{2}(\frac{1}{\lambda }{F}_{\theta }^{-1}{\nabla }_{\theta }J(\theta ){)}^{\top }{F}_{\theta }(\frac{1}{\lambda }{F}_{\theta }^{-1}{\nabla }_{\theta }J(\theta ))=\delta \\ & \lambda =\sqrt{\frac{2\delta }{{\nabla }_{\theta }J(\theta {)}^{\top }{F}_{\theta }^{-1}{\nabla }_{\theta }J(\theta )}}\end{array}$$

이렇게 closed-form 으로 gradient 를 수행하면 natural gradient 에 해당한다.

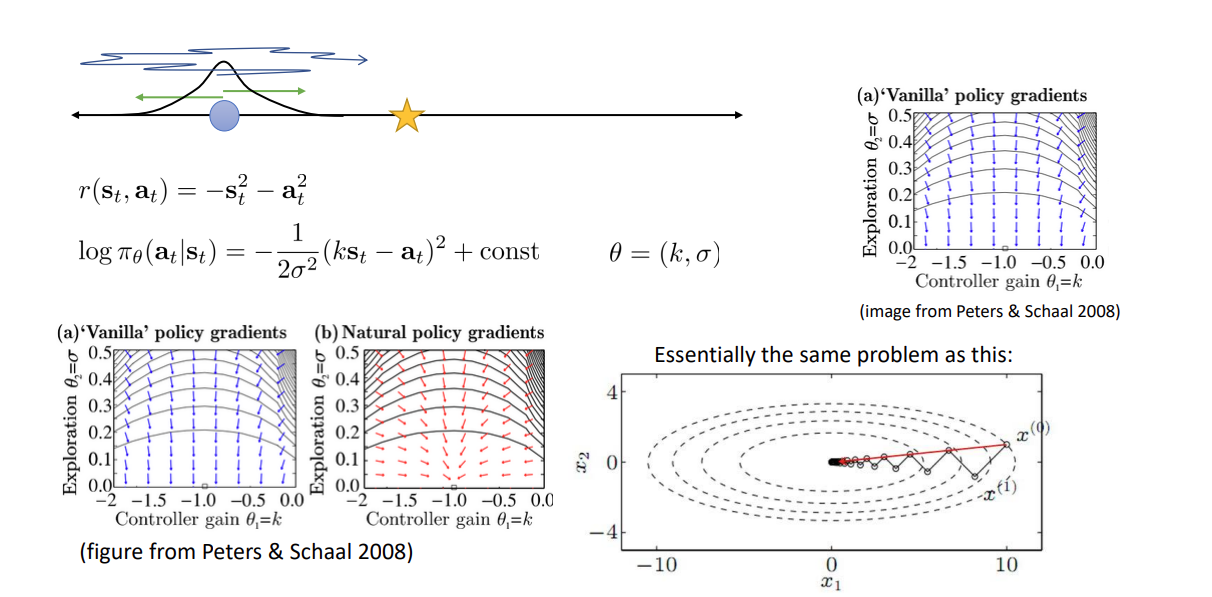
원 논문에서 이미지를 보면 Vanilla PG 에서의 ill-conditioned 가 natural PG 에선 훨씬 개선된 것을 알 수 있다.

Practical methods and notes