[CS275] 8. Deep RL with Q-Functions

Lecture 8: Deep RL with Q-Functions

이전에 Value Function Methods 를 다루었는데 이번에는 실제로 Deep RL 에서 Q function 을 어떻게 사용하는지 다룬다.

Value based 방식이 수렴성을 보장하지 않는다는 것을 알았지만, 실용적으로는 굉장히 잘 되게 만들 수 있고 유용한 방식이다.

Part 1

What’s wrong in online Q-learning?

이전 시간에 배웠듯이, Q-learning 에서 3번 step 은 target value ${\mathbf{y}}_i$ 에 대해서는 chain rule 을 적용하지 않았기 때문에 gradient descent 가 아니다.

Correlated samples in online Q-learning

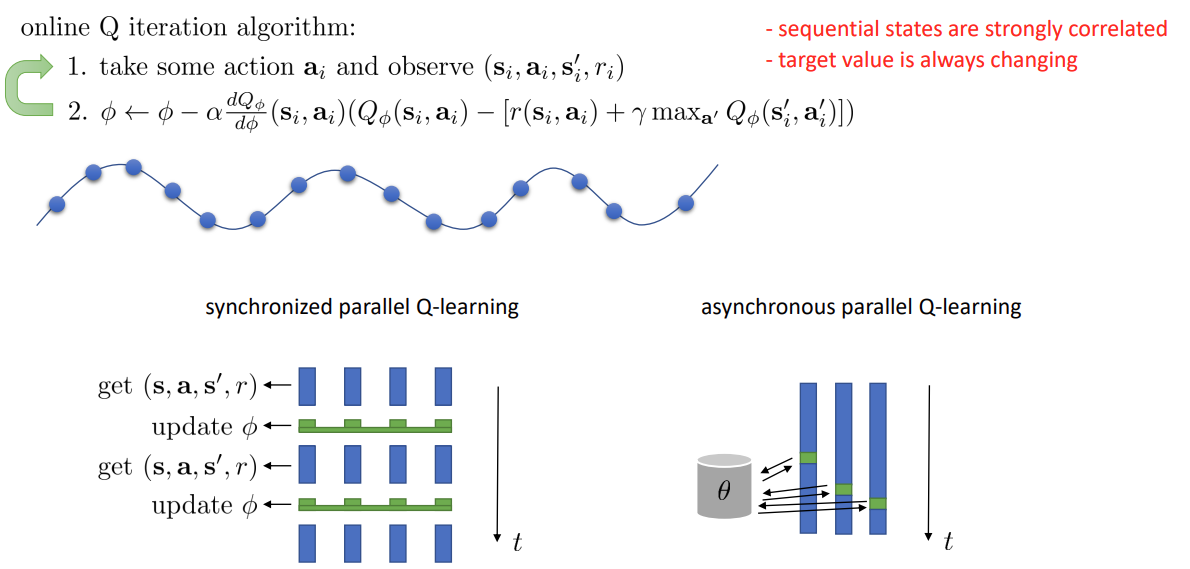
online Q iteration 의 step 1 을 보면, 연속적인 state $s_i,s_{i+1}$ 은 서로 가까운 시점에 있기 때문에 연관성이 매우 높은 것을 생각할 수 있다.

그렇기에 step 2 에서 target value 를 계산할 때 매번 변하게 된다. 그래서 매 시점에 하기 보다는 어떤 window 안에 있는 state 끼리 계산을 하는 것이 전체 함수를 예측하는데 더 효과적일 것이다.

사진의 아래 부분과 같이 synchronized / asynchronous parallel Q-learning 방식을 사용할 수 있다.

Another solution: replay buffers

Replay buffer 는 99년도에 제안된 오래된 방식이지만 제시된 문제를 해결할 수 있는 방법 중 하나이다.

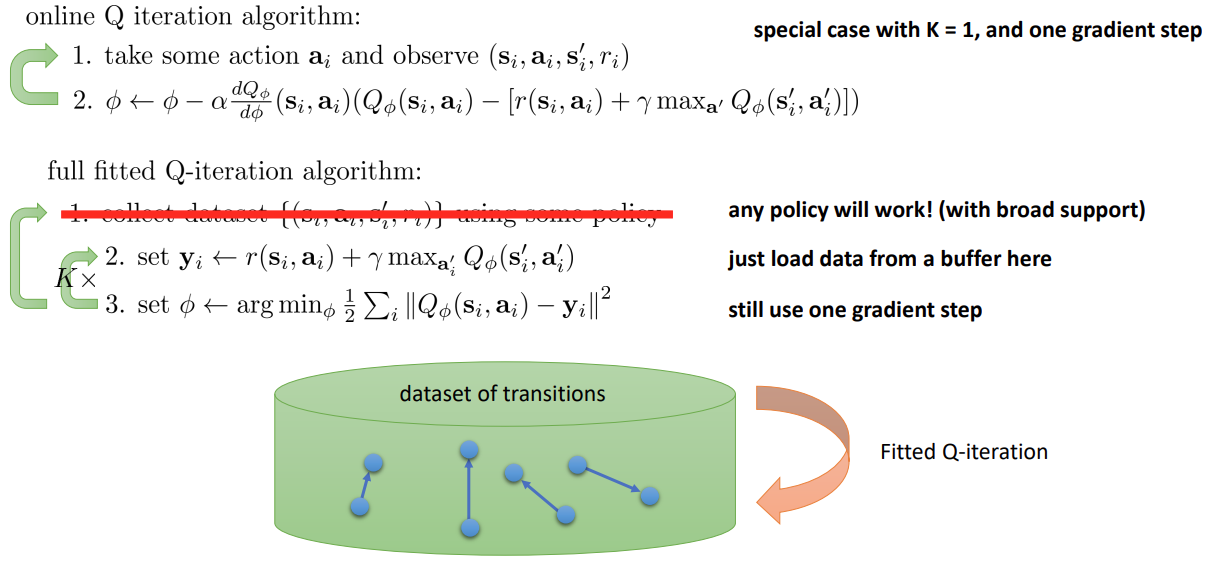
online Q iteration 을 full FQI 에서 K=1 인 경우로 생각한다면,

아래의 FQI 알고리즘에서 데이터셋에서 iteration 을 하지 않고, 단순히 buffer 에서 데이터를 가져와서 iteration 을 수행할 수 있다.

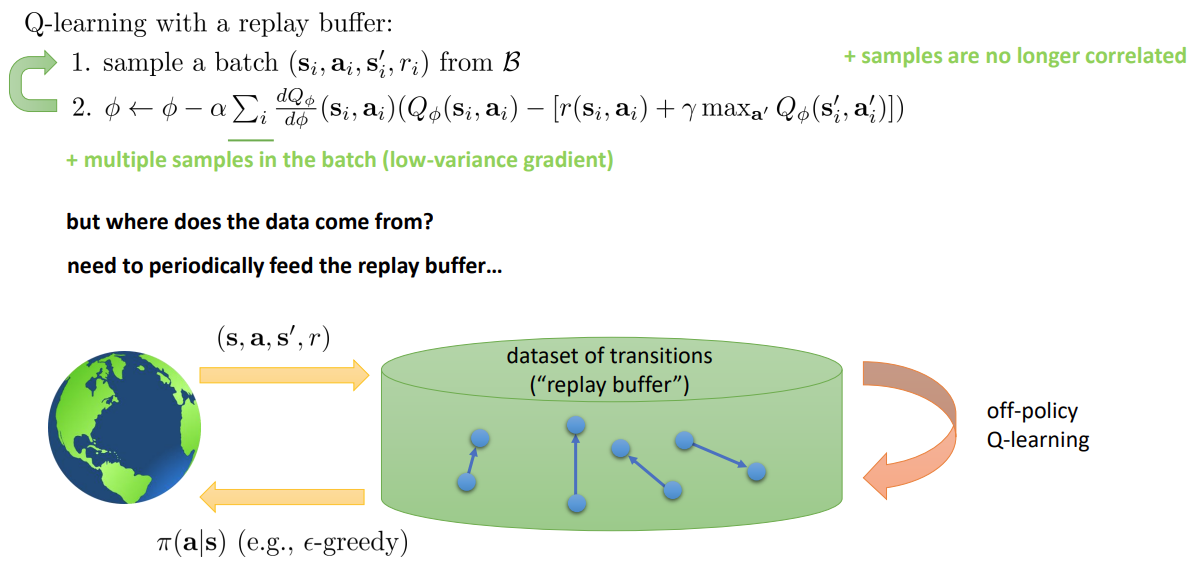
이렇게 하면 더이상 샘플들이 연관성을 가지지 않고, 여러 개의 샘플을 한번에 사용하여 분산을 낮출 수 있다.

초기의 policy 는 좋지 않기 때문에 개선된 최신의 policy 를 이용해 replay buffer 를 주기적으로 채워주어야 한다.

Part 2: Target Networks

Part 1 에서는 correlated 된 sample 문제를 해결하였다.

하지만 gradient descent 가 아닌 문제는 아직 해결되지 않았다. 본 파트에서는 해당 내용을 다룬다.

Q-Learning and Regression

Replay buffer 를 활용한 Q-learning 알고리즘에서 일반적으로 $K=1$ 를 선택한다. 이유는 잘못된 target value 로 gradient 를 여러 번 수행하며 좋지 않기 때문이다.

Fitted Q-iteration 에서 $\varphi$ 를 업데이트 하는 방식은 잘 구성되어있기 때문에 우리는 이 중간 정도의 적절한 수식을 구성해야 한다.

Q-Learning with target networks

Target value 가 계속해서 바뀌는 문제를 해결하기 위해 target network 를 사용한다. Target network 의 파라미터를 ${\varphi }^{\prime }$ 으로 하고 매우 큰 숫자의 $N$ 을 사용하면 이전과 유사한 Q-learning 이지만 target value 를 거의 변하지 않게 할 수 있다.

그리고 step 2~4의 이러한 모습은 supervised regression 과 유사하다.

”Classic” deep Q-learning algorithm (DQN)

classic 한 DQN 은 이전에 설명한 알고리즘에서 $K=1$ 의 모습이다. 즉, $\varphi$ 의 update 를 여러 번 iteration 하지 않고 한 번씩 만 update 한 후에 새로 sample 을 뽑는 것이다.

Alternative target network

classic DQN 은 위 이미지의 그림에서 볼 수 있듯이, target network 의 ${\varphi }^{\prime }$ 와 $\varphi$ 간 의 step 차이가 일정하지 않다. ${\varphi }^{\prime }$ 업데이트가 일어난 직후에는 1 step 의 차이만 있지만, 업데이트 직전에는 $N-1$ step 의 차이가 있기 때문이다.

그래서 가까이에서 보기에는 target network 가 움직이는 것 처럼 보이지만, 멀리서 보기에는 가만히 있는 것처럼 보인다. 이러한 방식은 약간의 의문을 갖게 한다.

이를 해결하기 위해, 컨벡스 최적화에서 개념을 가져와 Polyak averaging 과 유사한 방식을 활용한다. 물론, 이러한 방식 또한 신경망의 파라미터를 공유하는 것처럼 보이지만 실제로는 이론적으로 타당함을 어느정도는 보일 수 있다고 한다.

Part 3: A General View of Q-Learning

Part 2 에서 배웠던 알고리즘을 조금 더 넓은 관점에서 살펴보고자 한다.

Fitted Q-iteration and Q-learning

위에 보인 Q-learning 과 아래의 Fitted Q-learning 은 step 1과 2의 순서가 다른 것을 알 수 있다.

DQN 의 경우는 FQI 에서 $N=1,K=1$ 인 경우라고 생각할 수 있다.

A more general view

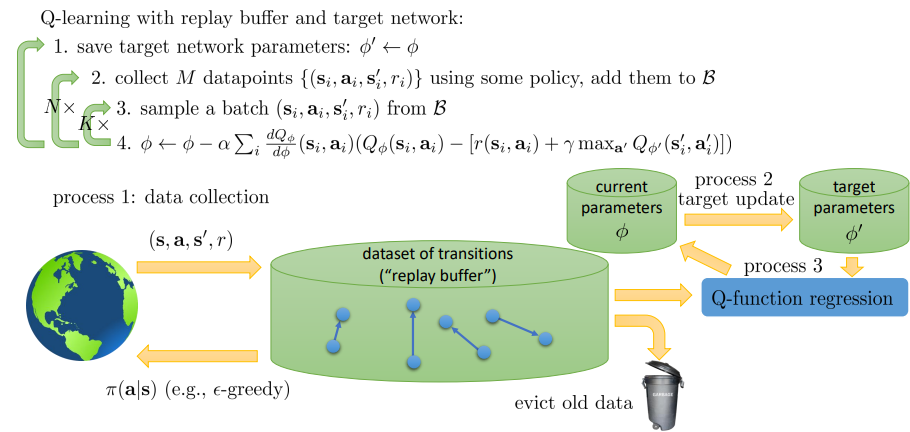
이를 하나의 개요도로 생각을 해보면,

1. 데이터 수집: 환경으로 부터 데이터를 수집해서 replay buffer $\mathcal{B}$ 에 넣는다. 이 때, 우리는 언제를 기준으로 이전 데이터를 버릴 지도 정해야 한다.
2. 파라미터 업데이트: target value $Q_{\varphi }^{\prime }$ 를 위한 ${\varphi }^{\prime }$ 는 $\varphi$ 로 부터 업데이트 된다. 이 과정은 매우 드물게 일어나서, target value 를 GD 과정에서는 일정하게 유지되도록 한다.
3. $Q$ regression: 알고리즘의 step 3,4 에 해당하는 단계이다. 갖고 있는 transition 과 $\varphi ,{\varphi }^{\prime }$ 를 통해 핵심이 되는 학습 과정이 일어난다.

그래서 이전에 배운 여러 Q-learning 알고리즘들이 서로 다르게 보이지만, 과정 1~3 이 어느정도의 비율로 이루어지는 지에 대한 차이라고 생각할 수 있다.

• Online Q-learning: evict immediately, process 1, process 2, and process 3 all run at the same speed
• DQN: process 1 and process 3 run at the same speed, process 2 is slow (quite large $\mathcal{B}$)
• Fitted Q-iteration: process 3 in the inner loop of process 2, which is in the inner loop of process 1

Part 4: Improving Q-Learning

Overestimation in Q-learning

예상하는 Q 가 증가할수록, return $R$ 도 증가하는 것은 맞지만 실제의 Q 값과는 큰 차이가 생긴다. 그 이유는 우리가 target value 를 계산할 때 $\max$ 를 취하는 부분이 문제가 된다.

이를 이해하기 위한 예시로 두 랜덤변수 $X_1,X_2$ 를 들었다. 평균이 0인 정규분포를 따른다고 생각해보자.

$X_1,X_2$ 중 하나라도 양수일 확률은 75% 이다. 그렇다면 $E[\max (X_1,X_2)]$ 는 양수를 가지게 될 것이다. $E[X_1],E[X_2]$ 는 기댓값이므로 모두 평균인 0을 갖게 된다. 이렇듯, $\max$ 를 취하게 되면 $Q_{{\varphi }^{\prime }}$ 를 추정함에 있어 양의 오차를 고려하게 되어 overestimate 하게 된다.

${\max }_{a^{\prime }}{Q}_{{\varphi }^{\prime }}(s^{\prime },a^{\prime })$ 를 구할 때 오차로 인해, 더 좋다고 잘못 추정한 ${\mathbf{a}}^{\prime }$ 를 선택하게 되면 target value 를 위한 값도 오차를 갖게 된다. 만약, 우리가 action selection 과 value estimation 의 오차를 decouple 시킬 수 있다면 이러한 문제를 해결할 수 있을 것이다.

Double Q-learning

“double” Q-learning 은 action 을 선택하는 것과 value 를 추정하는 데에 같은 신경망을 사용하지 않고, 다른 2개의 신경망을 사용하는 것이다.

$$\begin{array}{r}{Q}_{{\varphi }_A}(s,a)\leftarrow r+\gamma Q_{{\varphi }_B}(s^{\prime },\arg \underset{a^{\prime }}{\max }{Q}_{{\varphi }_A}(s^{\prime },a^{\prime }))\\ Q_{{\varphi }_B}(s,a)\leftarrow r+\gamma Q_{{\varphi }_A}(s^{\prime },\arg \underset{a^{\prime }}{\max }{Q}_{{\varphi }_B}(s^{\prime },a^{\prime }))\end{array}$$

Double Q-learning in practice

우리가 Double Q-learning 을 실제로 도입할 때 2개의 Q-function 을 사용하는 대신, 현재와 target network 를 사용한다.

하지만 우리가 이전에 다뤘듯, ${\varphi }^{\prime }$ 와 $\varphi$ 는 완전히 분리되어 있지 않다. 주기적으로 ${\varphi }^{\prime }$ 로 update 되기 때문이다. 그래도 완벽한 방식은 아니지만 훨씬 잘 작동한다고 한다.

Multi-step returns

$Q_{{\varphi }^{\prime }}$ 가 좋지 않은 학습 초기에는 return $r_{j,t}$ 를 주요하게 사용하는 것이 좋을 것이고, 반대의 경우에는 $Q_{ph{i}^{\prime }}$ 를 주요하게 사용하는 것이 좋을 것이다.

그래서 actor-critic 에서 했던 것처럼, $N$-step return estimator 개념을 사용해볼 수 있을 것이다.

Q-learning with N-step returns

N-step return 을 사용하는 Q-learning 방식의 장점은 학습 초기에 잘못된 $Q$ 를 적게 사용하여 less biased 되는 것이고, 덕분에 빨리 잘 학습된다는 것이다. 하지만 같은 policy 로 학습하는 on-policy 의 경우에만 정확하다는 것이다. 그래서 off-policy 의 데이터로 이 방식을 사용하는 것은 정확하지 않다.

이를 해결하는 방식은 이미지를 참고하자.

Part 5: Q-Learning with Continuous Actions

Q-learning with continuous actions

간단한 해결방법으로는 연속적인 action space 에서 $(a_1,\dots ,a_N)$ 를 샘플링하는 것이다. 이런 방법은 매우 간단하면서도 효율적으로 병렬화 할 수 있다. 하지만, action space 가 매우 클 경우에는 부정확한 방식이다.

Stochastic optimization 보다 더 정확한 방법론들은 아래와 같다.

• cross-entropy method (CEM)
  • simple iterative stochastic optimization
• CMA-ES
  • substantially less simple iterative stochastic optimization

Quadratic function 같이 쉽게 최적화할 수 있는 함수를 사용하는 것도 또다른 방법이다.

마지막 옵션은 approximate maximizer 를 학습시키는 것이다.

그래서 ${\mu }_{\theta }(s)\approx \arg {\max }_a{Q}_{\varphi }(s,a)$ 가 되는 ${\mu }_{\theta }(s)$ 를 학습시키고, chain rule 를 이용해 파라미터 $\theta$ 를 업데이트 한다.

이를 제안한 DDPG 를 살펴보면 step 5 가 해당 내용이다.

Part 6: Implementation Tips and Examples

Simple practical tips for Q-learning

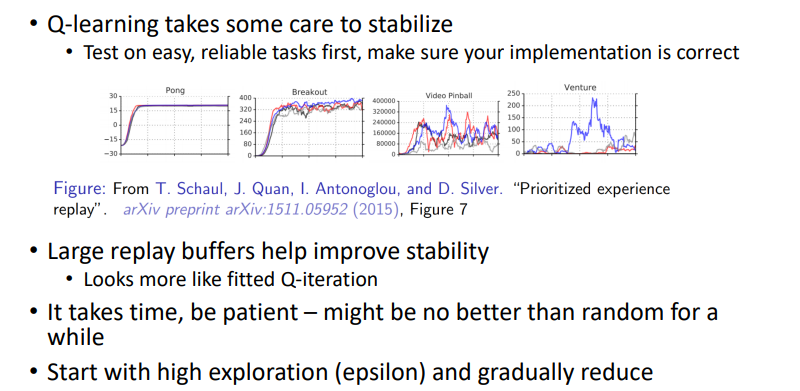
Q-learning 은 그림에서 보다시피 task 에 따라 매우 다른 양상을 보임을 알 수 있고, 같은 알고리즘도 경우에 따라 다른 양상을 보인다.

그렇기 때문에 쉬운 task 부터 디버깅, 파라미터 튜닝을 하며 문제를 풀어나가는 것이 좋다.

그리고 대다수의 경우 Q function 이 좋지 않기 때문에 오랜 시간을 지켜보며, 처음에는 exploration 을 많이 수행하는 것이 좋다.

Advanced tips for Q-learning

Q-learning suggested readings