[CS285] 7. Value Function Methods

Lecture 7: Value Function Methods

이전 시간에는 Actor-Critic 에 대해 배워보았다.

Part 1

Can we omit policy gradient completely?

Value function $V^{\pi }$ 는 어떤 ${\mathbf{s}}_t$ 가 가장 좋은지 알려주기 때문에, 단순히 더 큰 $V^{\pi }$ 를 얻는 action ${\mathbf{a}}_t$ 를 선택하게 하면 되므로 명시적인 policy neural network 가 필요하지 않을 수 있다.

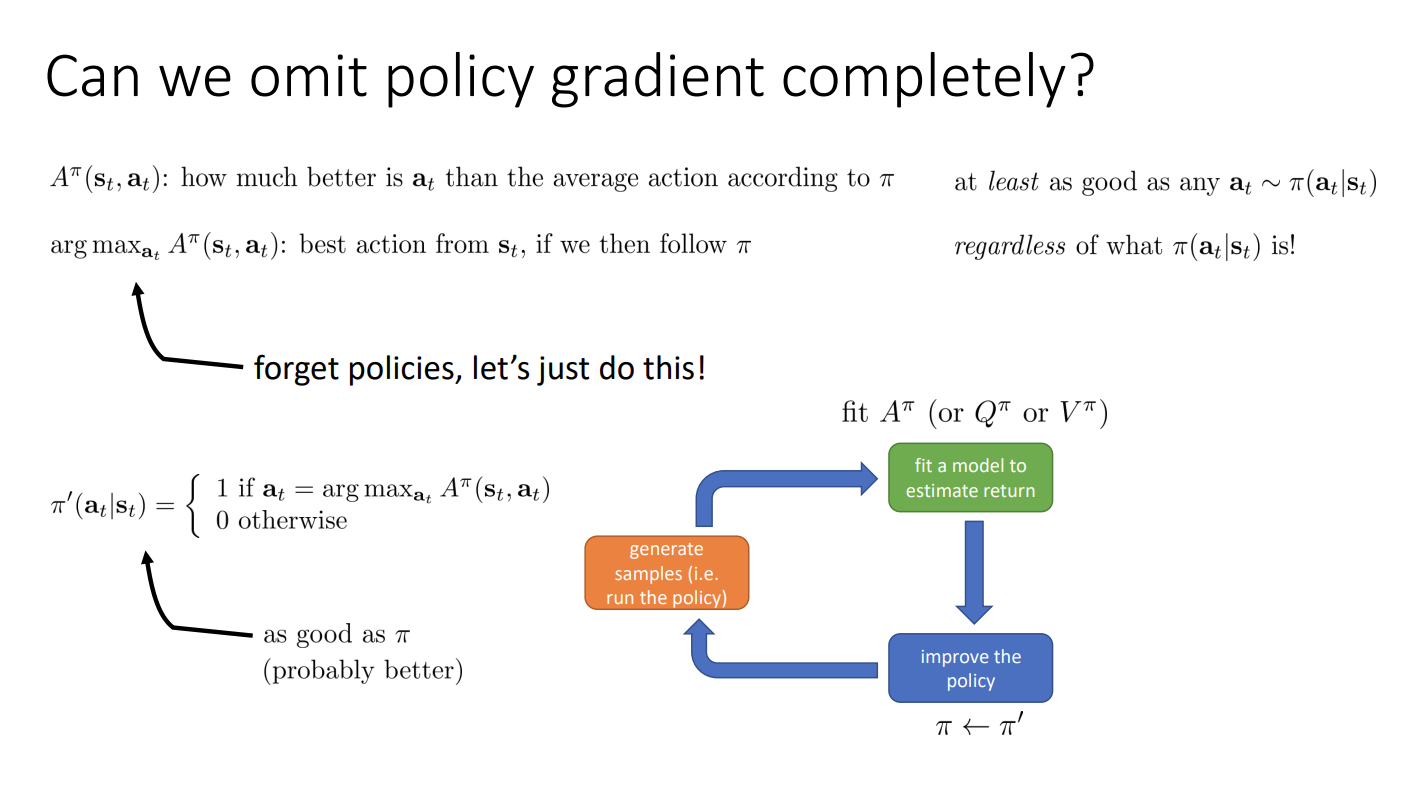
수식적으로 표현하면 $A^{\pi }$ 를 가장 최대화하는 action ${\mathbf{a}}_t$ 를 선택하자는 것이다. 이런 방식은 선택된 어떤 ${\mathbf{a}}_t$ 보다 같거나 좋게 되고, policy $\pi ({\mathbf{a}}_t|{\mathbf{s}}_t)$ 에 상관없이 가장 좋은 ${\mathbf{a}}_t$ 를 선택하게 된다.

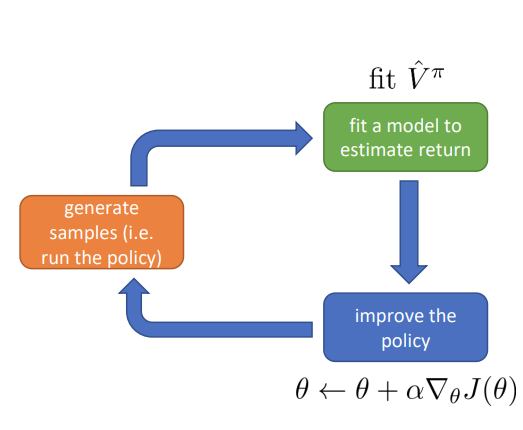
이전의 Actor-Critic 알고리즘과 비교해보면 더이상 policy gradient 를 수행할 필요 없이 policy improvement 를 수행할 수 있다.

Policy iteration

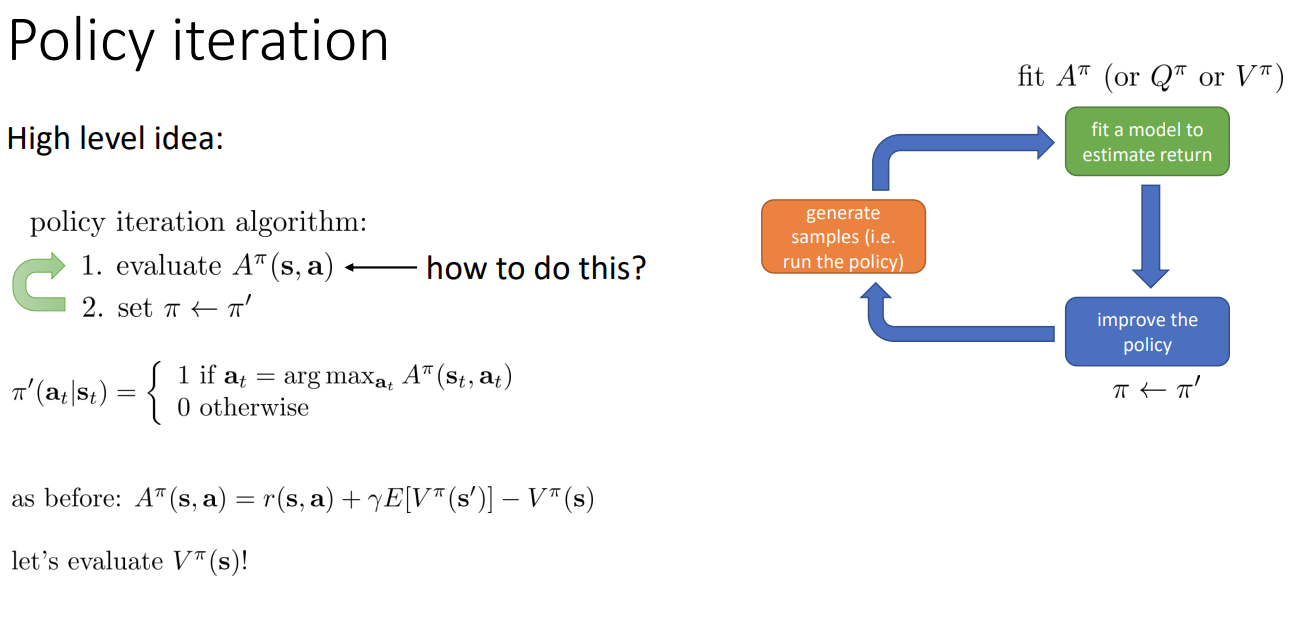
전체 알고리즘을 정리하면 위의 그림과 같다. 여기서의 문제는 ${\mathbf{A}}^{\pi }(\mathbf{s},\mathbf{a})$ 가 어떤 것이 가장 좋은지 어떻게 평가할 것인가 이다.

이전에 advantage function ${\mathbf{A}}^{\pi }(\mathbf{s},\mathbf{a})$ 를 평가한 방식을 보면 ${\mathbf{V}}^{\pi }(\mathbf{s})$ 를 평가하면 된다.

Dynamic programming

위와 같은 tabular MDP 에서는 transition probability $p({\mathbf{s}}^{\prime }|\mathbf{s},\mathbf{a})$ 를 알기 때문에 iteration 을 통해 optimal policy 를 쉽게 구해낼 수 있다.

Policy iteration with dynamic programming

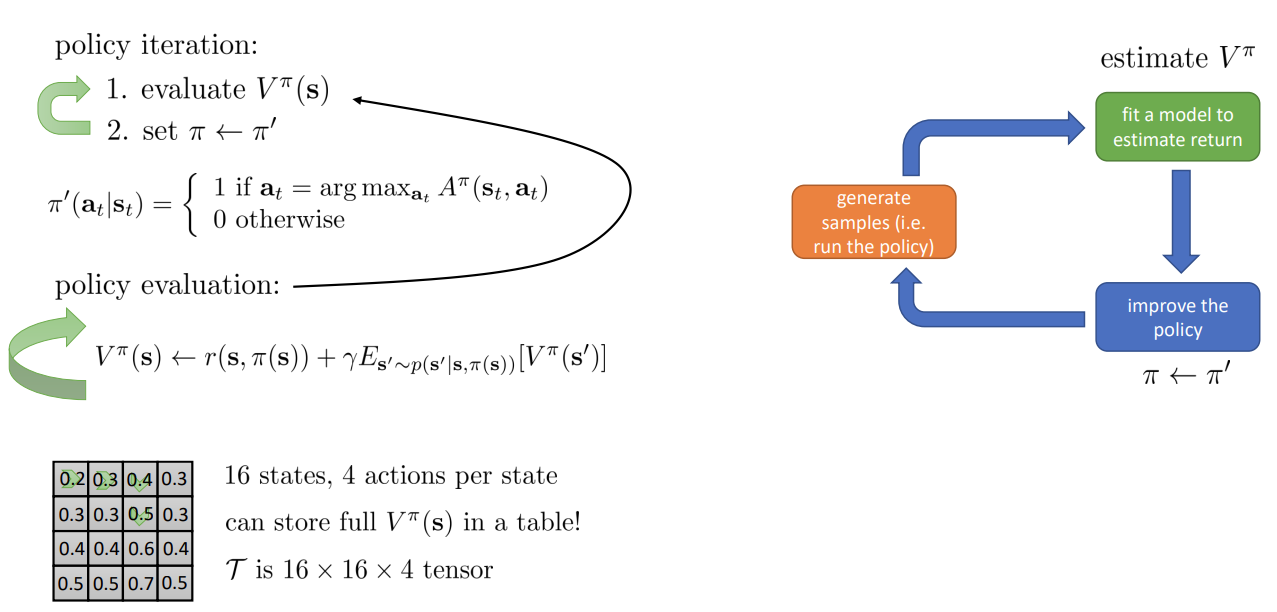
Tabular MDP 환경에서는 위 알고리즘 대로 policy evaluation 과 iteration 을 각 state 마다 수행하면 된다.

Even simpler dynamic programming

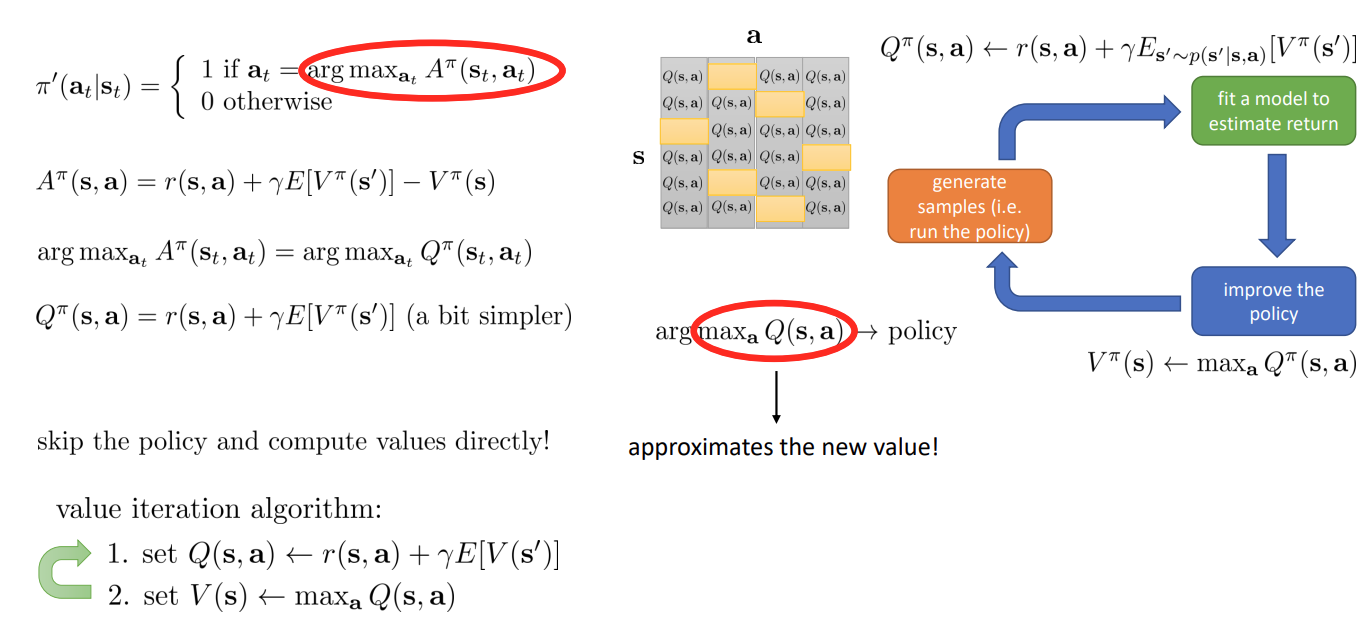
우리가 policy evaluation 을 수행할 때 $\arg {\max }_{{\mathbf{a}}_t}{A}^{\pi }(s_t,a_t)$ 를 계산하고 있다. 이 때, 우리는 ${\mathbf{a}}_t$ 를 찾고 있기 때문에 이와 관련되어 있지 않은 항인 $-V^{\pi }(\mathbf{s})$ 는 지워져도 관계 없다.

따라서 $\arg {\max }_{{\mathbf{a}}_t}{A}^{\pi }(s_t,a_t)=\arg {\max }_{{\mathbf{a}}_t}{Q}^{\pi }(s_t,a_t)$ 가 성립함을 알 수 있고, 이를 구하는 것이 더 쉬워진다. ($V^{\pi }(\mathbf{s})$ 를 구할 필요가 없어진다.)

$\arg {\max }_{\mathbf{a}}Q(\mathbf{s},\mathbf{a})$ 가 policy 를 구하는 것과 같으므로 policy 를 따로 구할 필요 없이 ${\max }_{\mathbf{a}}Q(\mathbf{s},\mathbf{a})$ 를 이용해서 value $V(\mathbf{s})$ 를 바로 구할 수 있다.

위 사진을 보면 $Q(\mathbf{s},\mathbf{a})$ 테이블을 구성해서 ${\max }_{\mathbf{a}}Q$ 로 $V(\mathbf{s})$ 를 얻은 후 이를 반복해서 알고리즘을 수행할 수 있음을 알 수 있다.

Part 2: Fitted Value Iteration & Q-Iteration

Fitted value iteration

이전과 달리 더 큰 환경에서 신경망을 활용하는 경우를 생각해보자.

이러한 경우 state space 의 dimension 이 매우 커지기 때문에 연산이 매우 커짐을 알 수 있다. 그래서 function approximator 를 사용한다. 이전 6강 에서 다루었듯이 neural network $V_{\varphi }:\mathcal{S}\to \mathbb{R}$ 를 사용한다.

What if we don’t know the transition dynamics?

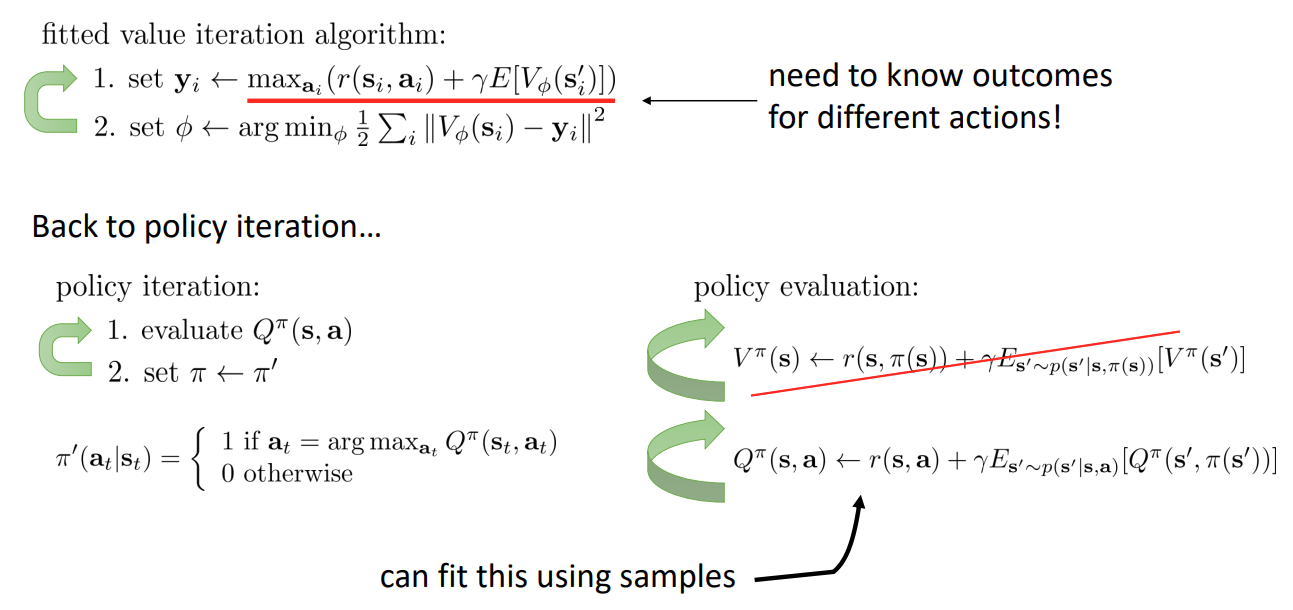
슬라이드에서 볼 수 있듯이 빨간 밑줄에서 transition dynamics 를 알아야 $\max$ 를 구할 수 있다.

그래서 $V^{\pi }$ 를 평가하는 대신 $Q^{\pi }$ 를 평가하면 이러한 문제를 피할 수 있다. 이전에 Policy iteration 와 비교해보면, 수식을 대체해서 사용된 것을 알 수 있다. $\mathbb{E}$ 를 계산할 때도 $p({\mathbf{s}}^{\prime }|\mathbf{s},\mathbf{a})$ 에서 샘플하기 때문에 더이상 policy $\pi$ 는 중요하지 않음을 알 수 있다.

그래서 수식을 약간 바꾼 것처럼 보이지만 transition dynamics 를 알지 못해도 policy iteration 을 수행할 수 있게 된다.

Can we do the “max” trick again?

fitted Q iteration 알고리즘의 단점은 non linear function approximation 에서는 수렴성이 보장되지 않는다는 것이다.

Fitted Q-iteration

아래 신경망 구조에서 input 에 $\mathbf{s},\mathbf{a}$ 가 들어가 있지만, 이렇게 하지 않고 input 에는 state $\mathbf{s}$ 만 들어가고 output 에 각 action $\mathbf{a}$ 에 따른 $Q_{\varphi }(\mathbf{s},\mathbf{a})$ 를 나오게 하기도 한다.

Part 3: From Q-Iteration to Q-Learning

Why is this algorithm off-policy?

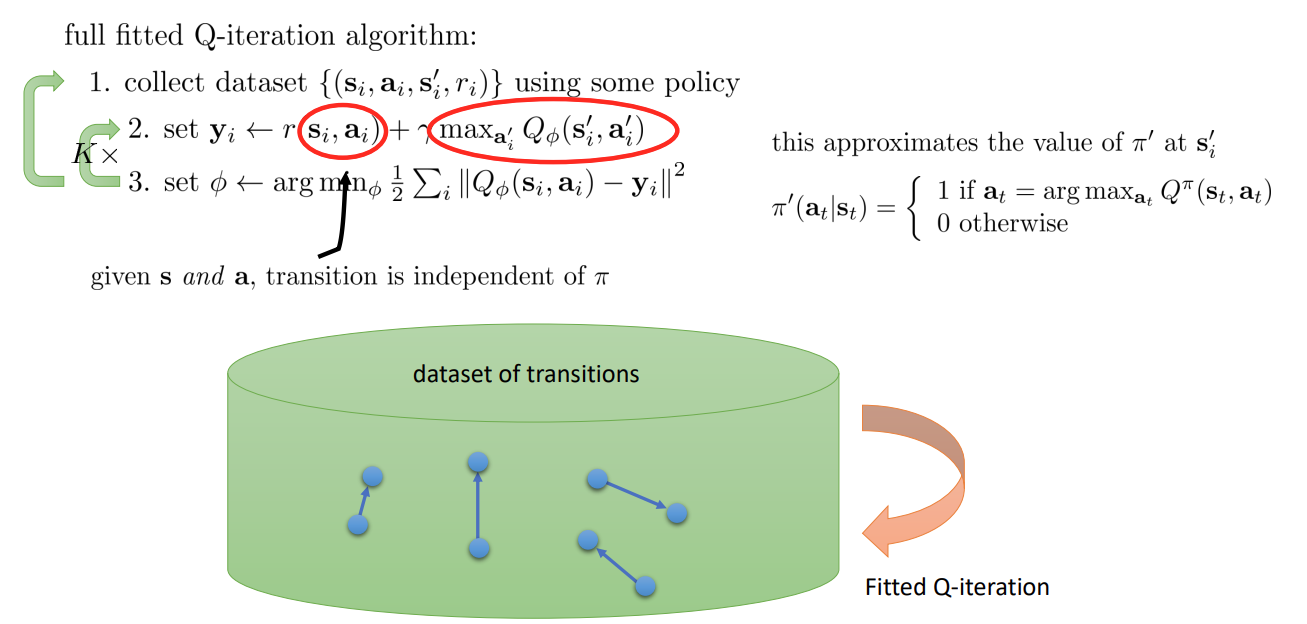
What is fitted Q-iteration optimizing?

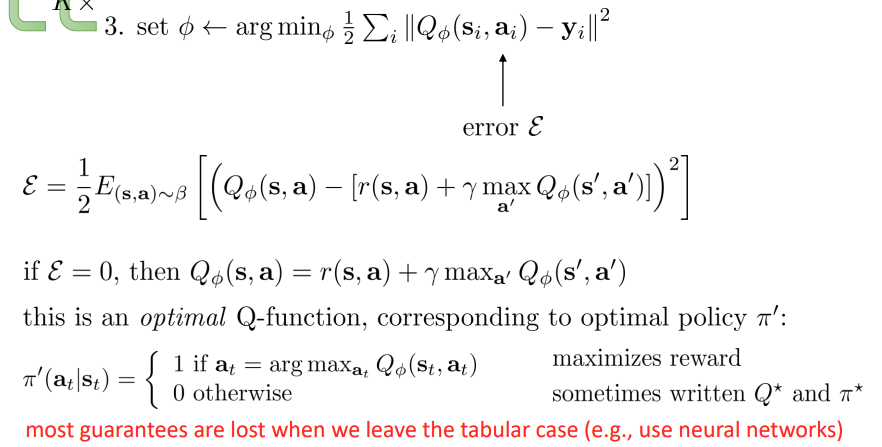
FQI 알고리즘에서 수식 3번을 보면 그림에 표현된 error $\epsilon$ 를 러닝을 통해 줄이는 것이 되고, $\epsilon =0$ 이면 optimal Q-function, policy ${\pi }^{\prime }$ 를 얻게 된다.

하지만 그렇지 않은 경우에는 policy 가 어떠한지 lost 한 상태가 된다.

Online Q-learning algorithms

이전의 FQI 는 $K$ 번 iteration 을 반복하고 추가적으로 데이터를 수집하는 방식을 사용했으나, 아래와 같이 online 방식으로 Q iteration 을 할 수 있다.

수식 3번에서 처럼 chain rule 을 이용하여 temporal difference 를 구하고 parameter 를 update 한다.

그리고 action ${\mathbf{a}}_i$ 를 선택할 때 off policy 이므로 이전처럼 greedy 한 방식 대신 다양한 policy 를 사용할 수 있다.

Exploration with Q-learning

우리의 최종 policy 는 FQI 처럼 greedy policy 일 것이다.

하지만 학습이 진행될 때 greedy policy 를 사용하는 것은 좋은 방법이 아니다. 왜냐하면, greedy policy 를 사용할 때 초기의 어떤 임의의 안좋은 Q function 이 사용되고 있다면 특정 state $s_t$ 에서는 계속 안좋은 action $a_t$ 를 만들 것이고 거기에 stuck 하게 될 것이다.

그래서 더 좋은 action 이 있는지 Exploration 을 수행해야 한다. 이를 위해 약간의 무작위성을 추가한다.

Part 4: Value Function in Theory

Value function learning theory

value iteration algorithm 이 수렴하는지? 그렇다면, 어떤 것으로 수렴하는지? 에 대한 이론적 설명을 하기 위해 Bellman operator $\mathcal{B}$ 를 사용한다.

optimal 한 $V\ast$ 에 도달할 수 있음을 증명할 수 있는데, 이유는 $\mathcal{B}$ 가 contraction 이기 때문이다.

Non-tabular value function learning

이제 value iteration algorithm 을 $\mathcal{B}$ 를 이용해 아래 이미자와 같이 간단하게 표현할 수 있다.

non-tabular 한 경우에는 fitted value iteration 을 사용한다는 것을 Part 2 에서 배웠다. 기존의 방식의 step 2 를 $\mathcal{B}$ 를 이용해 표현한 수식은 아래와 같다.

$$V^{\prime }\leftarrow \arg \underset{V^{\prime }\in \Omega }{\min }\frac{1}{2}\Sigma \Vert V^{\prime }(s)-(\mathcal{B}V)(s){\Vert }^2$$

파란 색 실선은 value function $V$ 가 표현될 수 있는 모든 집합 $\Omega$ 를 의미한다. 그래서 $\mathcal{B}V$ 는 해당 실선에서 벗어나게 되므로 다시 projection 을 하는 operator $\Pi$ 가 필요하다.

$$\Pi :\Pi V=\arg \underset{V^{\prime }\in \Omega }{\min }\frac{1}{2}\Sigma \Vert V^{\prime }(s)-V(s){\Vert }^2$$

그래서 non-tabular 환경에서의 fitted value iteration 은 $\mathcal{B}$ 와 $\Pi$ 를 이용해 다시 표현된다. (그림 참고)

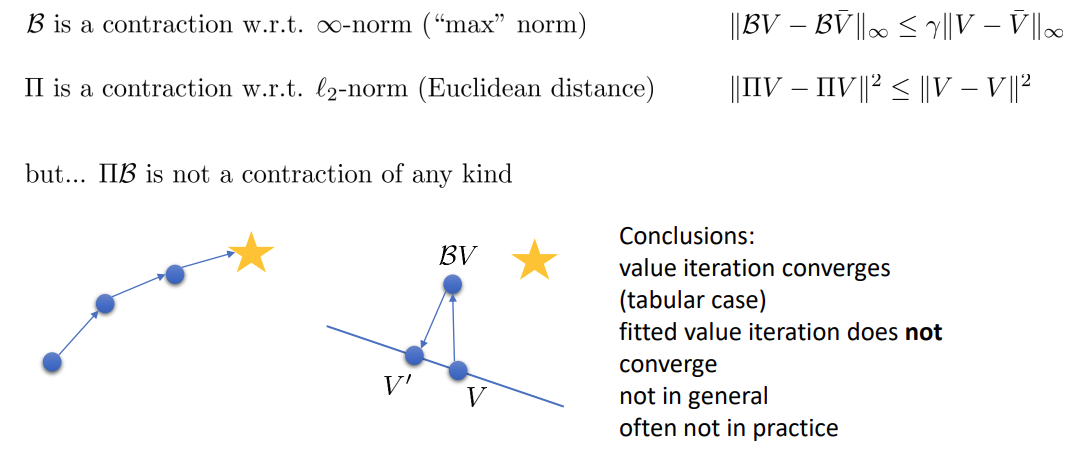
$\mathcal{B}$ 와 $\Pi$ 모두 contraction 이지만 $\Pi \mathcal{B}$ 는 contraction 이 아니다. 그래서 fitted value iteration 은 수렴성이 보장되지 않고, 실제로는 더욱 잘 되지 않는다.

What about fitted Q-iteration?

이전과 동일한 방식으로 $\mathcal{B}$ 와 $\Pi$ 를 정의할 수 있다.

그렇다면, $Q\leftarrow \Pi \mathcal{B}Q$ 로 FQI 를 단순히 표현할 수 있다.

FVI 와 마찬가지로 $\Pi \mathcal{B}$ 는 constraction 이 아니다.

But… it’s just regression!

그렇다면 이전에 설명한 대로 online FQI 는 regression 이므로 수렴하지 않느냐 하는 질문이 생길 수 있다.

하지만 Q-learning 은 실제로는 gradient descent 가 아니다! 왜냐하면 target value ${\mathbf{y}}_i$ 에도 $Q_{\varphi }$ 가 있지만 이 항에 대해서는 gradient 를 계산하지 않기 때문이다.

이와 마찬가지로 이전에 다루었던 batch actor-critic algorithm 도 수렴성이 보장되지 않는다.