[CS285] 6. Actor-Critic Algorithms

Lecture 6: Actor-Critic Algorithms

Part 1

State & state-action value functions

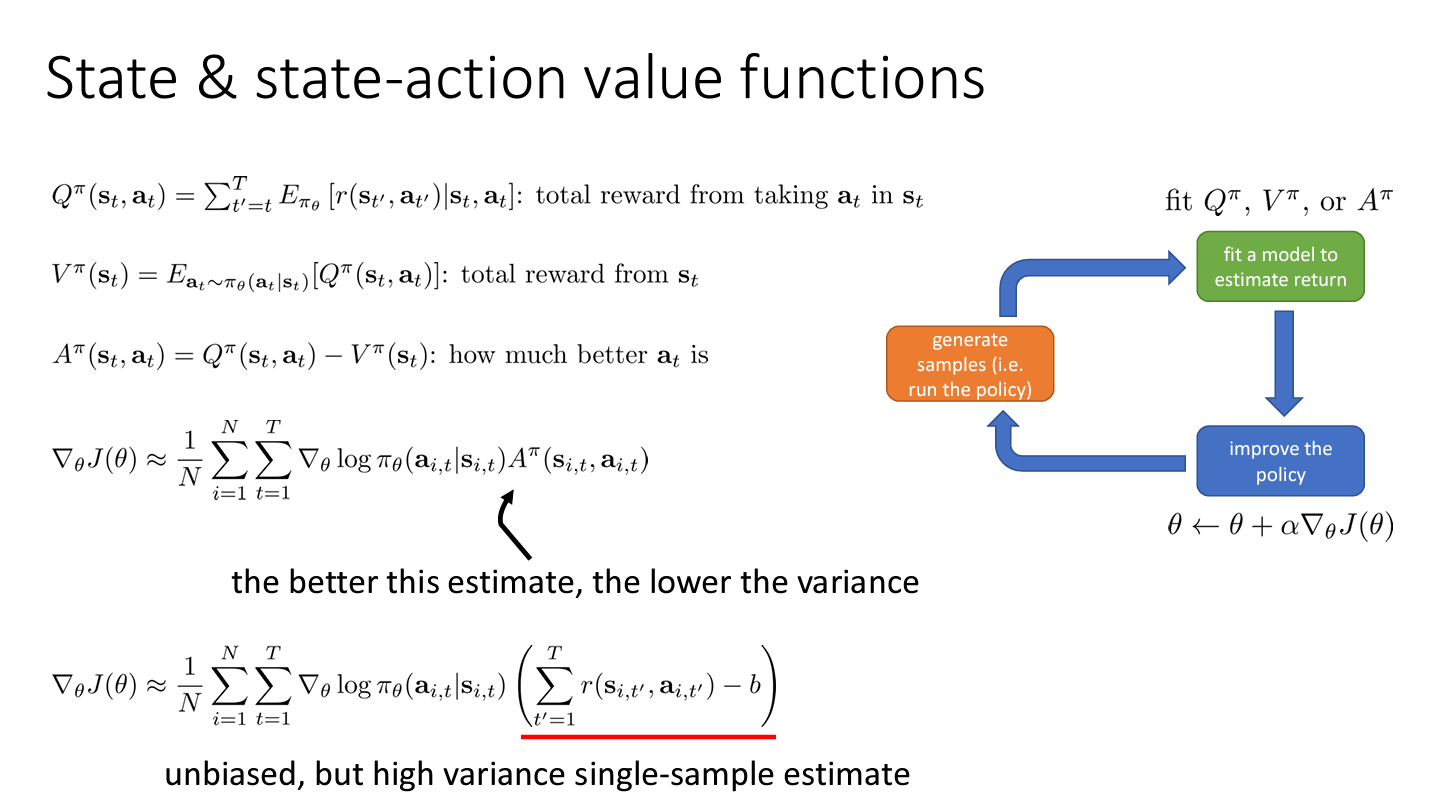
Value function fitting

위 3개의 value function 중 어떤 것에 맞춰야 할까?

$$\begin{array}{rl}{Q}^{\pi }(s_t,a_t)& =\sum _{t^{\prime }=t}^T{E}_{{\pi }_{\theta }}[r(s_{t^{\prime }},a_{t^{\prime }})|s_t,a_t]\\ & =r(s_t,a_t)+\sum _{t^{\prime }=t+1}^T{E}_{{\pi }_{\theta }}[r(s_{t^{\prime }},a_{t^{\prime }})|s_t,a_t]\\ & =r(s_t,a_t)+E_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}[V^{\pi }(s_{t+1})]\\ & \approx r(s_t,a_t)+V^{\pi }(s_{t+1})\end{array}$$

$Q^{\pi }$ 를 위와 같이 유도하여 근사식 (4) 을 세울 수 있다. 그럼 이제 $A^{\pi }(s_t,a_t)\approx r(s_t,a_t)+V^{\pi }(s_{t+1})-V^{\pi }(s_t)$ 로 정리해볼 수 있다. 이렇게 되면 오로지 $V^{\pi }$ 에 의존하게 되고 이는 $s_t$ 만 가지고 얻을 수 있기 때문에 $Q^{\pi }$ 나 $A^{\pi }$ 보다 구하기 쉽다. (학습하기 쉽다)

나중에는 $Q^{\pi }$ 를 맞추기 위한 Actor Critic 도 배우지만 우선 $V^{\pi }$ 를 다루기로 한다.

Policy evaluation

$V^{\pi }={\sum }_{t^{\prime }=t}^T{E}_{{\pi }_{\theta }}[r(s_{t^{\prime }},a_{t^{\prime }})|s_t]$ 로 정의되므로 $t=1$ 일 때의 $V^{\pi }$ 를 구하는 것으로 목적함수를 표현할 수 있다.

$$J(\theta )=E_{s_1\sim p(s_1)}[V^{\pi }(s_1)]$$

그렇다면 policy evaluation 을 어떻게 할 수 있을까? 가장 먼저 제시된 것은 Monte Carlo policy evaluation 이다.

기댓값을 사용하는 대신 여러 번 샘플링한 보상의 평균을 구해 다음과 같이 근사한다. (많은 궤적을 얻을 수록 평균은 기댓값에 수렴해간다)

$$V^{\pi }(s_t)\approx \frac{1}{N}\sum _{i=1}^N\sum _{t^{\prime }=t}^{T}r(s_{t^{\prime }},a_{t^{\prime }})$$

4.1. Policy Evaluation

Monte Carlo evaluation with function approximation

이제 신경망에 이를 적용시켜서 $y^{\prime }:s\to {\hat{V}}^{\pi }(s)$ 을 학습시키고자 한다.

하지만 policy gradient 를 수행하기 전에 모델이 맞도록 해야한다. 같은 $s_t$ 를 두 번 가는 경우 그 이후의 궤적이 크게 달라지더라도 같은 ${\hat{V}}^{\pi }$ 를 추정할 것이기 때문이다.

평균을 내는 방식보다는 안 좋지만 그래도 여전히 좋다고 한다. Why?

그래서 학습 데이터 $\{(s_{i,t},y_{i,t}={\sum }_{t^{\prime }=t}^{T}r(s_{i,t^{\prime }},a_{i,t^{\prime }})\}$ 으로 supervised regression $\mathcal{L}(\varphi )=\frac{1}{2}{\sum }_i\Vert {\hat{\mathcal{V}}}_{\varphi }^{\pi }(s_i)-y_i{\Vert }^2$ 를 수행한다.

+) generalization 으로 인해 낮은 분산을 가진다고 한다. ⇒ 정확하게 이해하지 못함.

5.1 Monte Carlo Policy Evaluation

Can we do better?

bootstrapped 방식은 single sample estimator 대신 $\hat{V}$ 를 사용하여 낮은 분산을 갖지만 ${\hat{V}}_{\varphi }^{\pi }$ 가 틀릴 수도 있기 때문에 높은 bias 를 가지기도 한다.

Part 2: From Evaluation to Actor Critic

Aside: discount factors

만약 episode 의 길이 $T$ 가 무한대라면 어떡할까? ${\hat{V}}_{\varphi }^{\pi }$ 가 무한대로 커지게 될 것이다.

따라서 이를 시간이 지날 수록 보상을 작게 만들어주고자 discount factor $\gamma \in [0,1]$ 를 도입한다.

$$y_{i,t}\approx r(s_{i,t},a_{i,t})+\gamma {\hat{V}}_{\varphi }^{\pi }(s_{i,t+1})$$

그리고 이러한 $\gamma$ 의 도입은 MDP 를 아래와 같이 state 의 종료가 도입된 것으로 볼 수 있다.

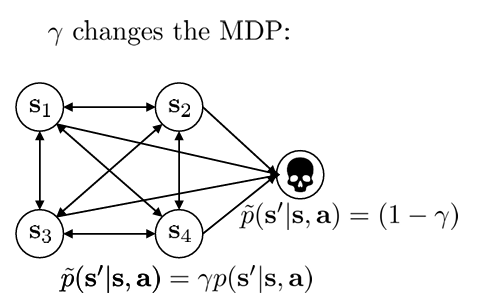
what about (Monte Carlo) policy gradients?

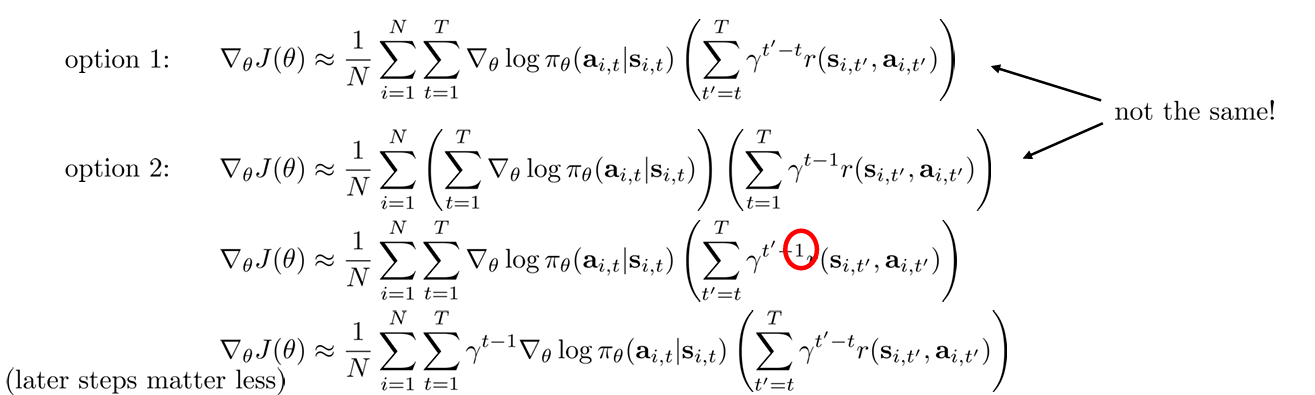
Policy gradient 를 생각해보았을 때 single sample 로 얻는 option 1 (”reward-to-go” 에서 유도함) 과 평균을 내는 Monte Carlo 방식의 option 2 를 모두 생각해볼 수 있다.

Option 1 과 option 2 는 수학적으로도 다른데, option 2 의 수식을 정리해보면 이는 미래의 gradient descent 에도 discount factor 를 적용시키는 것이다. 미래의 보상 뿐만 아니라 미래의 수행할 policy 도 현재의 미치는 영향이 적기 때문이다.

Which version is the right one?

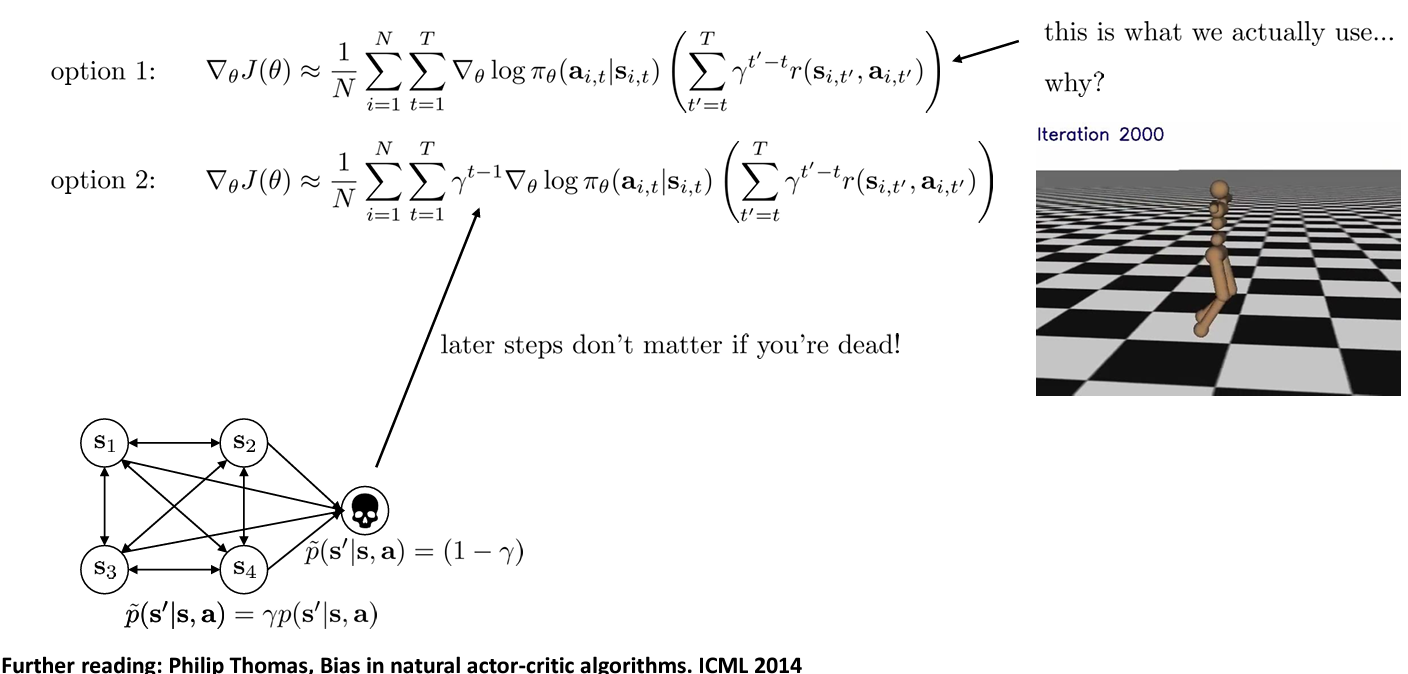
Actor-critic algorithms (with discount)

앞서 Part 2 첫 장에서 설명한 actor-critic 알고리즘에 discount factor $\gamma$ 가 3번째 step에 적용되었다.

Part 3: Actor-Critic Design Decisions

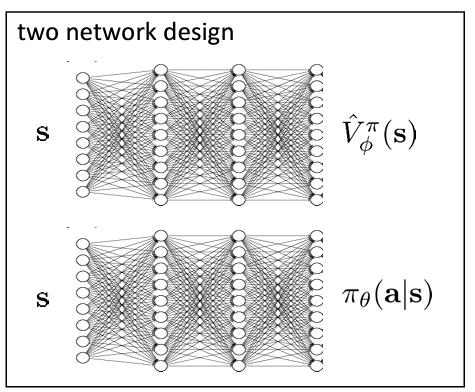
Actor-critic 에서는 actor ${\pi }_{\theta }(a|s)$ 와 critic ${\hat{V}}_{\varphi }^{\pi }(s)$ 모두 학습시켜야 한다.

이를 각각의 신경망으로 학습하는 것은 단순하고 안정적이지만, 서로 공유하는 것이 없다는 단점이 있다.

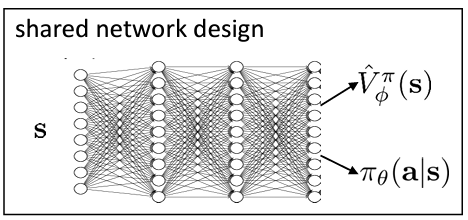
그래서 shared network design 으로 두 개를 한 번에 학습시키는 효율적인 방법도 있다. 하지만 서로 다른 gradient descent 를 수행하므로 unstable 하고 hyperparameter 에 민감할 수 있다.

Online actor-critic in practice

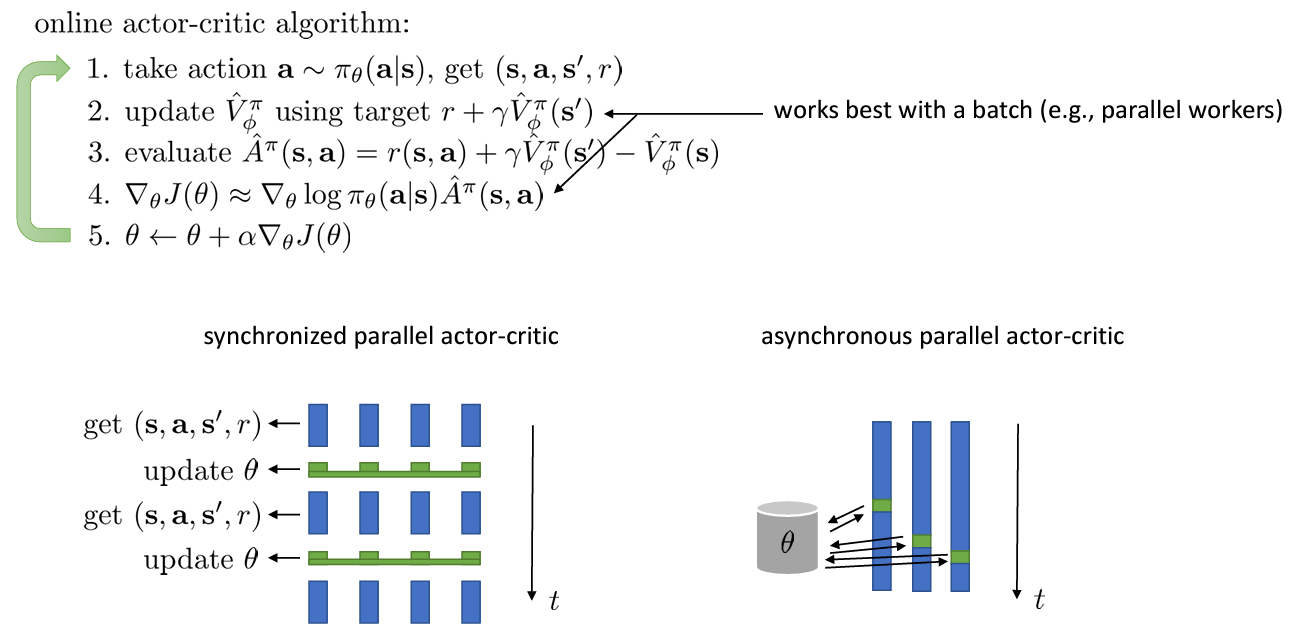
SGD 에서 하나 씩 update 하는 것은 비효율적이므로 여러 개의 actor 를 가지고 update 를 수행한다.

Can we remove the on-policy assumption entirely?

위에서 asynchronous 하게 수행하는 경우 이전의 actor 가 수행한 것으로 개선한 $\theta$ 를 가지게 된다는 문제가 있다.

그래서 얻은 데이터를 가지고 policy improvement 를 수행하고자 한다.

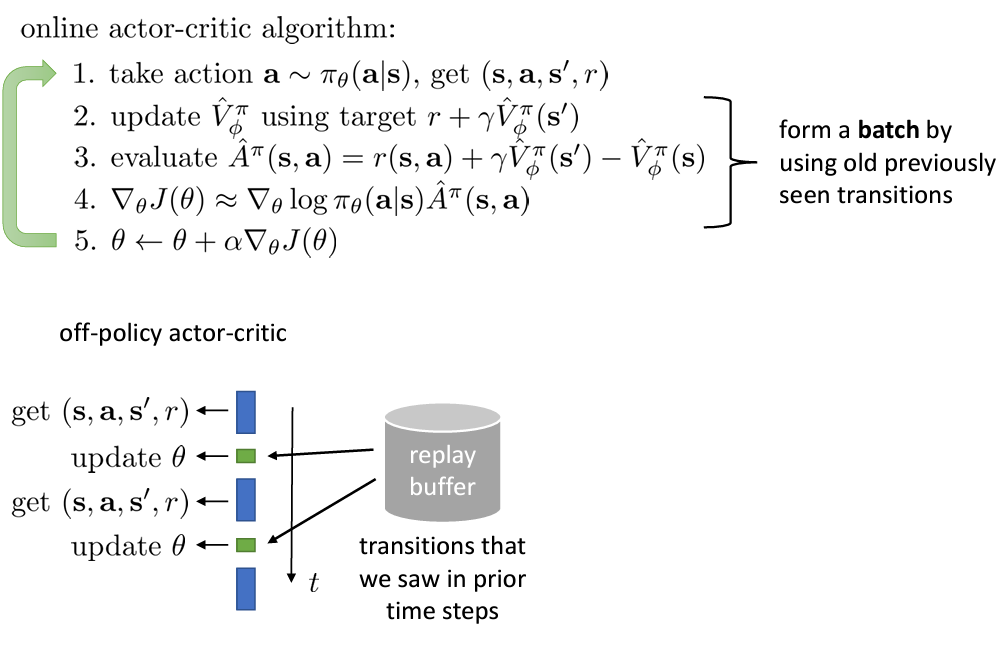
replay buffer 를 사용하여 ${\pi }_{\theta }$ 로 얻은 action $a$ 를 가지고 $(s,a,s^{\prime },r)$ 를 replay buffer 에 넣는다.

그리고 여기서 샘플링하여 ${\hat{V}}_{\varphi }^{\pi }$ 와 ${\hat{A}}^{\pi }$ 를 학습시거나 구한다.

문제는 step 3 와 5 에서 계산에서 사용되는 $a_i$ 나 $s_i^{\prime }$ 가 ${\pi }_{\theta }$ 에서 얻은 것이 아니기 때문에 ($\mathcal{R}$ 에서 추출한 것이므로) 수식을 수정해야 한다.

Fixing the value function

여기서부터 매우 어려워짐

$\mathcal{R}$ 에서 $\{s_i,a_i,r_i,s_i^{\prime }\}$ 만 가져온다. 따라서 이 외의 $i$ 가 붙은 것들은 같은 timestamp 이지만 replay buffer 에서 가져온 것이 아니다. 또한, $a_i$ 는 ${\pi }_{\theta }$ 에서 얻은 것이 아니다.

Step 3 를 수정하기 어떤 $a_t$ 이어도 상관없는 $Q^{\pi }$ 를 사용한다. ${\hat{V}}_{\varphi }^{\pi }(s_t^{\prime })$ 는 $s_t^{\prime }$ 에서 $\pi$ 를 수행할 때 얻을 보상인 반면, $Q^{\pi }(s_t,a_t)$ 는 given $s_t,a_t$ 에서 policy $\pi$ 를 수행했을 때 기대되는 보상이기 때문이다.

그래서 이제는 $\hat{V}$ 대신 $\hat{Q}$ 를 학습시킨다.

그러면 regression 에서의 target value $y_i$ 가 바뀌어야 한다. $V^{\pi }(s_t)$ 수식을 보면 policy $\pi$ 에서 취한 $a$ 에 대한 $Q$ 의 기댓값으로 표현되는 것을 알 수 있다. 이를 이용해 $a_i^{\prime }$ 을 이전의 (update 되지 않은) ${\pi }_{\theta }$ 로 부터 얻어 ${\hat{Q}}_{\varphi }^{\pi }$ 를 구하면 기존의 $y_i=r_i+\gamma {\hat{V}}_{\varphi }^{\pi }(s_i^{\prime })$ 을 $y_i=r_i+\gamma {\hat{Q}}_{\varphi }^{\pi }(s_i^{\prime })$ 로 바꿀 수 있다.

Fixing the policy update

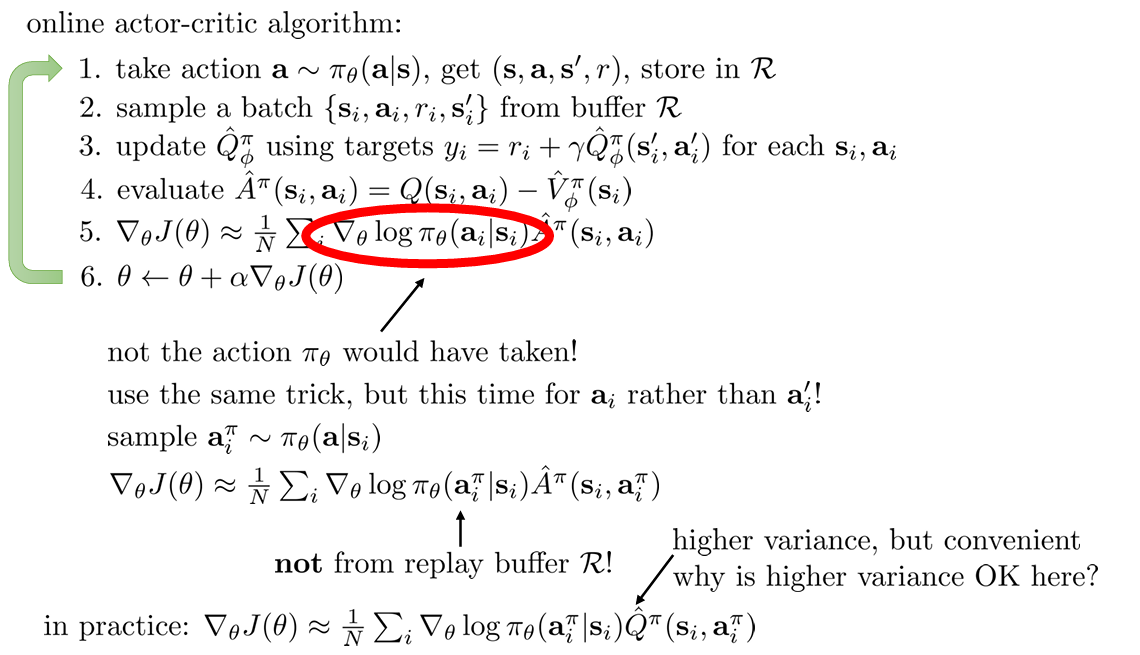
Step 5 도 마찬가지로 이전 ${\pi }_{\theta }$ 에서 $a_i^{\pi }$ 를 샘플링하여 얻는다.

또한 실제로 gradient 를 계산할 때 ${\hat{A}}^{\pi }$ 를 사용해도 상관없지만 ${\hat{Q}}^{\pi }$ 를 사용하는 것이 훨씬 편하고 좋다고 한다. 왜냐하면, ${\hat{Q}}^{\pi }$ 는 그 자체로는 높은 분산을 갖지만 off-policy 이므로 신경망으로 여러 번 샘플링하여 쉽게 분산을 낮출 수 있기 때문이다.

What else is left?

또 남은 문제로는 $s_i$ 가 $p_{\theta }(s)$ 로 부터 얻어지지 않았다는 점이다. 하지만 off-policy 에서는 근본적으로 이를 해결할 수 없다.

궁극적으로는 $p_{\theta }(s)$ 에서 최적의 policy ${\pi }^{\ast }$ 를 얻고자 한다. 이러한 ${\pi }^{\ast }$ 는 $p_{\theta }(s)$ 보다 수많은 $s$ 를 방문하여 replay buffer 에 넣어 더 넓은 분포를 가짐으로써 얻을 수 있다.

Some implementation details

실제로 적용할 때 step 4 에서 inegral 대신 reparameterization trick 을 사용할 수도 있고, $\hat{Q}$ 를 학습하기 위한 더 근사한 방법들도 많다.

예제로 들어준 알고리즘으로는 Soft Actor Critic (SAC) 가 있다.

• Haarnoja, Tuomas, et al. “Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor.” International conference on machine learning. PMLR, 2018. Arxiv Link

Part 4 Critics as Baselines

이번 파트에서는 critic 을 baseline $b$ 에 사용하여 얻는 trade-off 에 대해 다룬다.

Critics as state-dependent baselines

Actor-critic 과 policy gradient 에서의 baseline 을 사용하는 것의 장점을 모두 얻고자 함.

그래서 value function ${\hat{V}}_{\varphi }^{\pi }$ 를 (state-dependent) baseline 으로 사용함으로써 bias 없이 (actor-critic 만큼은 아니지만) 낮은 분산을 가지도록 함.

이는 $s_{i,t}$ 에 의존성을 가지고 있기 때문이라고 한다. 그래서 더 의존적이게($a_{i,t}$ 에도) 만들어 분산을 더 낮출 수도 있을까?

Control variates: action-dependent baselines

가능하지만 좀 더 문제가 복잡해진다.

state 와 action 에 모두 의존적인 baseline 을 “control variates” 라고 한다.

Eligibility traces & n-step returns

$${\hat{A}}_C^{\pi }(s_t,a_t)=r(s_t,a_t)+\gamma {\hat{V}}_{\varphi }^{\pi }(s_{t+1})-{\hat{V}}_{\varphi }^{\pi }(s_t)$$

Actor-critic 알고리즘의 Advantage estimator ${\hat{A}}_C^{\pi }$ 은 PG 보다 낮은 분산값을 갖지만 value 가 틀리다면 높은 bias 를 가진다.

$${\hat{A}}_{MC}^{\pi }(s_t,a_t)=\sum _{t^{\prime }=t}^{\infty }{\gamma }^{t^{\prime }-t}r(s_{t^{\prime }},a_{t^{\prime }})-{\hat{V}}_{\varphi }^{\pi }(s_t)$$

Monte-carlo PG 에서의 Advantage estimator ${\hat{A}}_{MC}^{\pi }$ 를 살펴보면 bias 가 없지만 하나의 샘플로 추정한 값이어서 높은 분산값을 갖는다.

그렇다면 이 두 가지를 합쳐서 사용할 수는 없을까?

이를 위해 n-step returns 를 사용한다. 시간이 지날수록 분산이 커지기 때문에 그 전까지의 보상만을 사용하고 나머지는 value function 을 사용한다.

$${\hat{A}}_n^{\pi }(s_t,a_t)=\sum _{t^{\prime }=t}^{t+n}{\gamma }^{t^{\prime }-t}r(s_{t^{\prime }},a_{t^{\prime }})-{\hat{V}}_{\varphi }^{\pi }(s_t)+{\gamma }^n{\hat{V}}_{\varphi }^{\pi }(s_{t+n})$$

따라서 $n>1$ 일 때 더 좋으며 n 이 커질수록 ${\gamma }^n$ 이 작아지므로 bias 는 작아지지만 분산은 커지게 된다. 따라서 앞부분 term 이 분산을 조절하고 뒷 term 이 bias 를 조절한다.

Generalized advantage estimation

그래서 나온 GAE 는 적절한 n 을 정하는 대신 n-step returns 의 가중치를 가해 더한 것이다.

$${\hat{A}}_{GAE}^{\pi }(s_t,a_t)=\sum _{n=1}^{\infty }{w}_n{\hat{A}}_n^{\pi }(s_t,a_t)$$

그렇다면 어떻게 가중치를 부여할까? 적은 분산을 위해서는 작은 n 이 좋기 때문에 $w_n$ 을 ${\lambda }^{n-1}$ 에 비례하도록 만들어 기하급수적으로 미래의 보상을 작게 만든다.

$${\hat{A}}_{GAE}^{\pi }(s_t,a_t)=r(s_t,a_t)+\gamma ((1-\lambda ){\hat{V}}_{\varphi }^{\pi }(s_{t+1})+\lambda (r(s_{t+1},a_{t+1})+\gamma (\dots ))$$

위 식을 간단하게 ${\hat{A}}_{GAE}^{\pi }(s_t,a_t)={\sum }_{t^{\prime }=t}^{\infty }(\gamma \lambda {)}^{t^{\prime }=t}{\delta }_{t^{\prime }}$ 으로 표현할 수 있다. 이 때 ${\delta }_{t^{\prime }}=r(s_{t^{\prime }},a_{t^{\prime }})+\gamma {\hat{V}}_{\varphi }^{\pi }(s_{t^{\prime }+1})-{\hat{V}}_{\varphi }^{\pi }(s_{t^{\prime }})$ 이다.

그래서 $\lambda$ 를 선택하여 biase 와 분산간의 trade-off 를 정하는 discount 의 역할을 한다.

Part 5. Review, Examples, and Additional Readings

Review

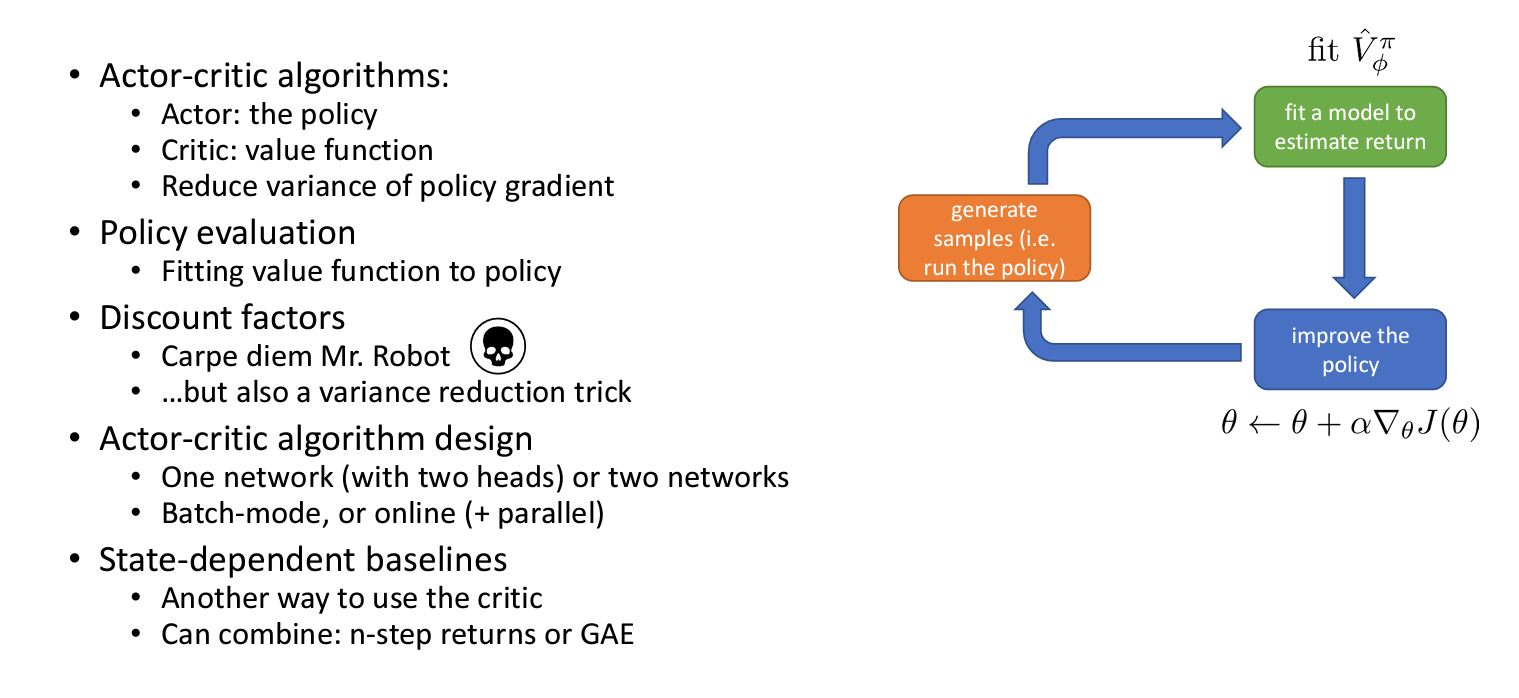
Actor-critic suggested readings

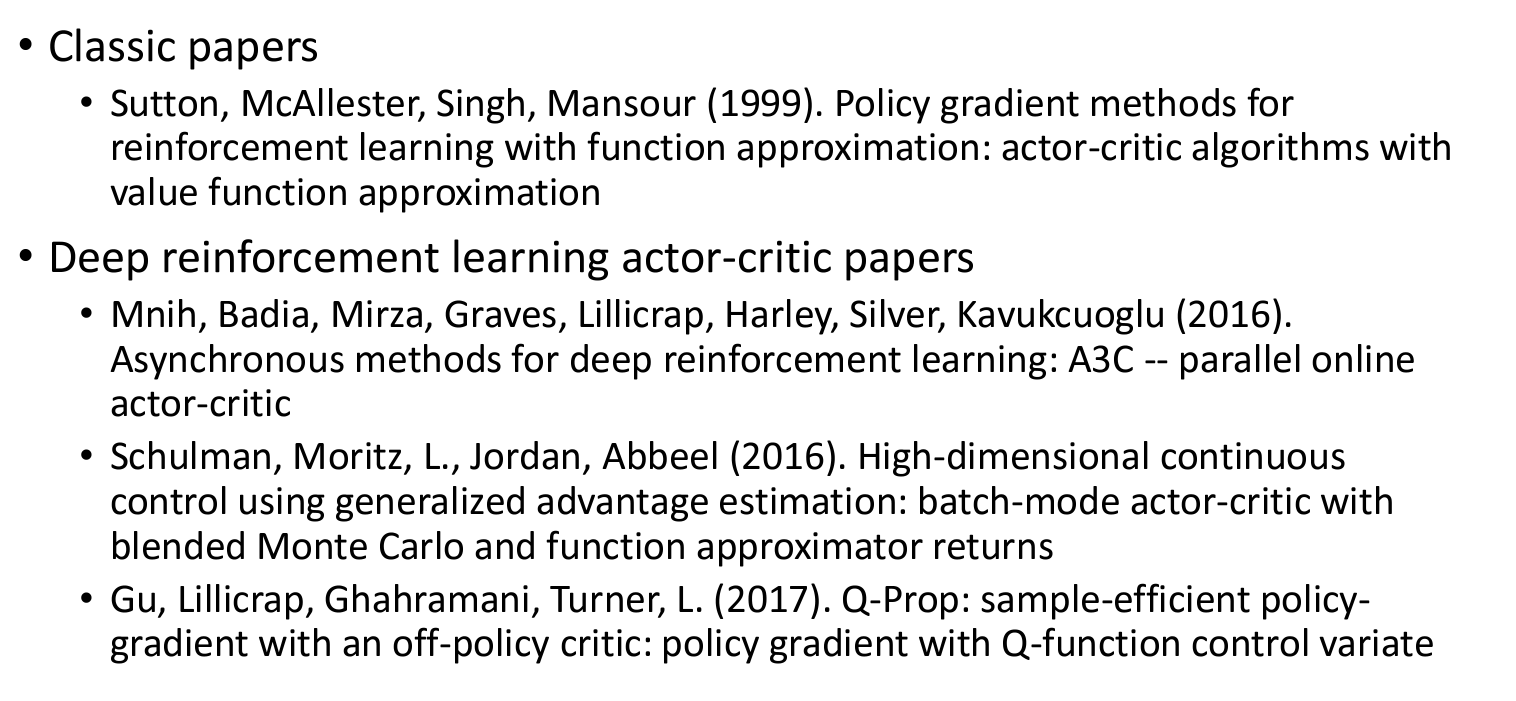
• Sutton, R. S., McAllester, D., Singh, S., & Mansour, Y. (1999). Policy Gradient Methods for Reinforcement Learning with Function Approximation. In S. Solla, T. Leen, & K. Müller (Eds.), Advances in Neural Information Processing Systems (Vol. 12). Retrieved from https://proceedings.neurips.cc/paper_files/paper/1999/file/464d828b85b0bed98e80ade0a5c43b0f-Paper.pdf
• Mnih, Volodymyr, et al. “Asynchronous methods for deep reinforcement learning.” International conference on machine learning. PMLR, 2016. Arixiv
• Schulman, John, et al. “High-dimensional continuous control using generalized advantage estimation.” arXiv preprint arXiv:1506.02438 (2015). Arxiv
• Gu, Shixiang, et al. “Q-prop: Sample-efficient policy gradient with an off-policy critic.” arXiv preprint arXiv:1611.02247 (2016). Arxiv