4. Policy Gradient (2)
이전에 다 살펴보지 못한 Policy Gradient를 강의 교안과 “수학으로 풀어보는 강화학습” 교재로 마저 공부하기로 했다.
The Goal of Policy Gradient Method
를 policy 로 생성되는 궤적, state-action의 연속적인 조합이라 하자.
이에 최적 파라미터 는 아래와 같다.
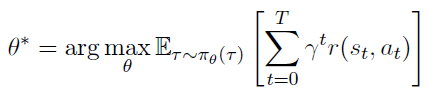
이 때 는 policy 로부터 얻은 궤적의 확률밀도함수(pdf) 이다. the p.d.f of trajectories from the policy
그러면 목적함수 를 아래와 같이 정의할 수 있다.
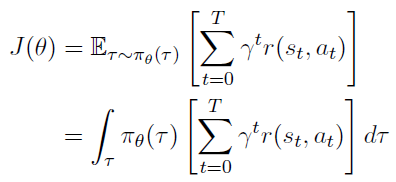
Compute
Bayes’ rule를 통해 를 계산해보자.
Bayes’ rule
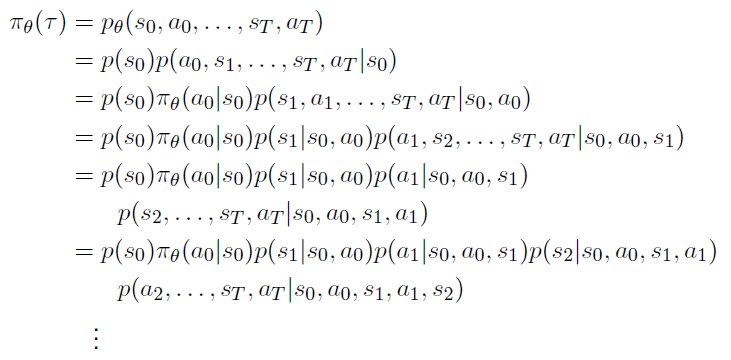
위에 정리된 수식에 Markov property를 적용하면 아래와 같이 식을 정리할 수 있다.
Markov property
즉, 이전 history에 대한 정보가 현재 state에 담겨있다고 보기 때문에 는 아래와 같이 정리된다.
Direct Policy Differentitaion
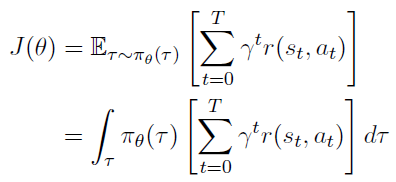
아까 본 목적함수에서 를 로 표현하자. 그리고 목적함수를 에 대해 미분하면 아래와 같다.
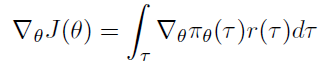
Likelihood Ratios
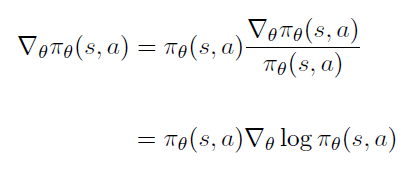
라는 가정을 사용하여 위의 목적함수 미분을 풀이한다.
이 가정은 (1) 를 샘플링할 수 있고, (2) 각 샘플된 값에 대해 와 를 평가할 수 있으면 사용 가능하다.
The likelihood-ratio gradient — Graduate Descent
이제 목적함수 미분을 정리하면 아래와 같다.,
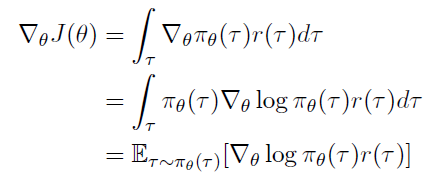
이전에 에 대해 얻었으므로 양쪽에 로그를 취해 마저 수식을 전개한다.
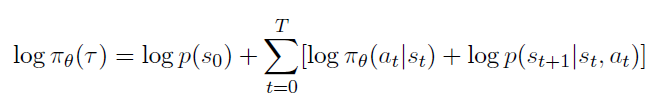
여기에 gradient를 취해준다 (에 대해 미분)
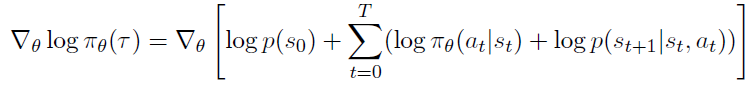
가 없는 term들은 미분했을 때 0이 되므로 지워지고 최종적으로는 아래와 같이 목적함수 미분이 정리된다.
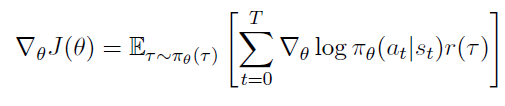
Evaluating the Policy Gradient
샘플링을 통해 목적함수를 근사해보자.
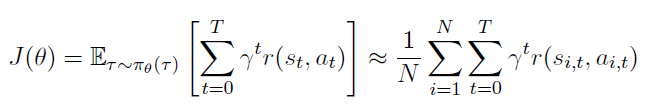
여기서 은 샘플된 궤적의 수이다.
목적함수의 그래디언트에도 적용할 수 있다.
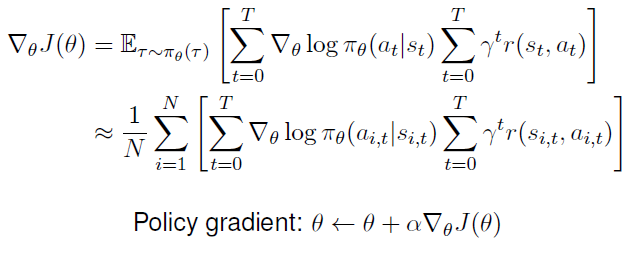
Softmax Policy
feature의 선형결합 을 이용한 weight action 개념이 사용된다.
action의 확률은 이 weight의 거듭제곱에 비례한다.
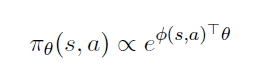
log-likelihood function의 1차 미분인 score function은 아래와 같다.
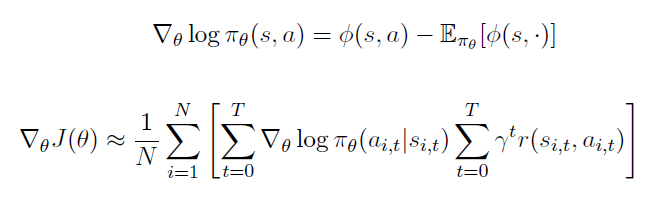
이에 대한 증명
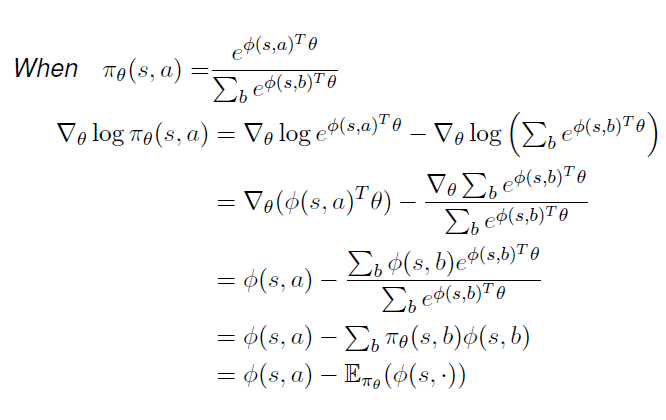
Gaussian Policy
연속적인 action 공간에서는 Gaussian policy를 사용한다.
평균(Mean)은 state feature의 선형 결합이다.
분산(Variance)는 로 고정하거나 변수화할 수 있다.
Policy는 Gaussian이다.
이에 대한 score function은 아래와 같다.
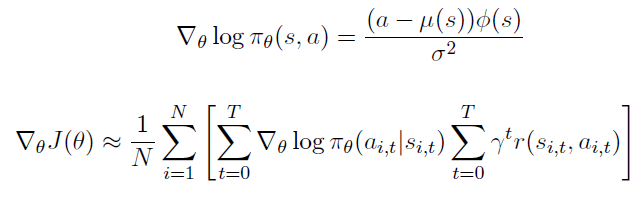
추가 참고자료
Monte-Carlo Policy Gradient (REINFORCE)
stochastic gradient ascent를 통해 파라미터를 업데이트하고, 의 unbiased sample로 return 를 얻는다.
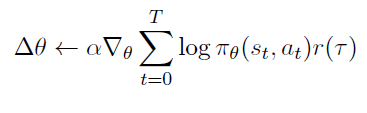
위 Evaluating the Policy Gradient에서 샘플을 이용해 기댓값을 근사한 것을 사용한다.
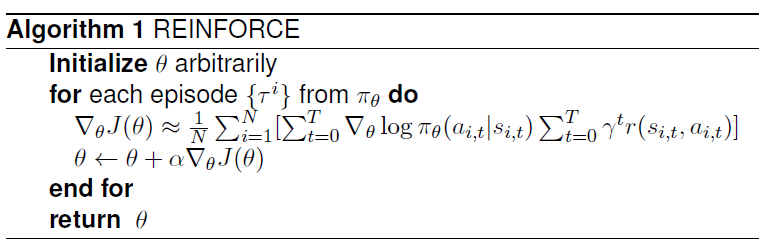
를 업데이트할 때 return을 고려하므로 return이 큰 policy가 더 큰 영향을 끼쳐, policy가 개선된다.
매번 에서 각 에피소드 를 뽑아서 사용하므로 (for each episode from policy do) 사용한 샘플은 더이상 쓰지 않고 새로 샘플을 생성한다.
Limitation of PG
Policy Gradient의 한계는 분산 값이 높다는 것이다. (High variance)
또한, 가 0인 경우에는 좋은 샘플 혹은 궤적을 얻음에도 불구하고 목적함수의 그래디언트가 사라지게 된다.
Reducing Variance
- Reward to go
인과성(Causality) timestep 에 실행된 policy는 이전 timestep들의 보상값에 영향을 끼치지 못한다.
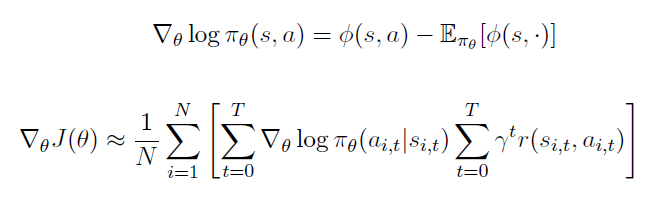
이를 이용해 reward (그리고 PG variance)를 작게 만들 수 있다.
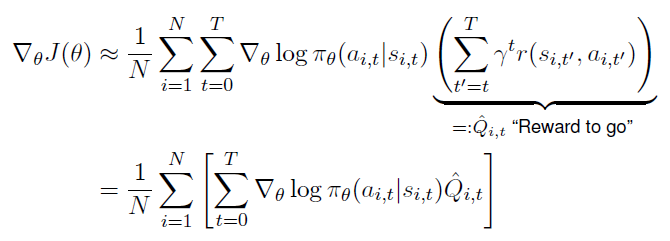
부터 고려하던 부분을 부터 고려하는 방식이다.
- a Baseline
Policy Gradient에서 baseline function 를 빼내어 기댓값의 변화 없이 분산을 줄이는 방식이다. (→ PG still unbiased!)
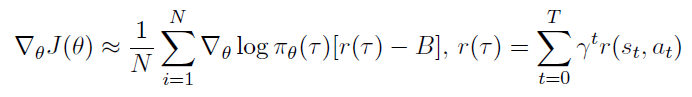
위 Policy Gradient 의 기댓값이 변화없음에 대한 증명
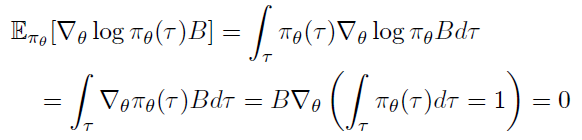
따라서 궤적 가 포함되지 않은 baseline을 선정해야하는데 좋은 baseline으로는 State-value function이 있다.
이를 이용해 advantage function 를 이용해 PG를 다시 정리할 수 있다.
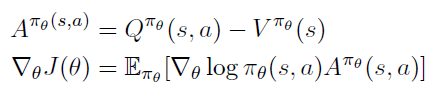
- a Critic
Critic을 통해 Action-value function을 추정할 수 있다.
Actor-critic 알고리즘은 두 파라미터 집합으로 구성된다.
Actor: critic으로 제안되는 방향으로 를 업데이트 한다.
Critic: 를 이용해 Action-value function을 업데이트한다.
그래서 다음과 같은 근사 PG를 사용한다.
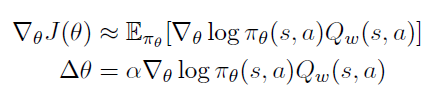
Estimating the Action-value Fuction
- Critic은 policy evaluation과 같은 문제를 푸는 것이다 (??)
- 현재의 에 대해 policy 가 얼마나 좋은지 본다
- least-squares policy evaluation 같은 것을 사용할 수 있다.
Actor-Critic Methods
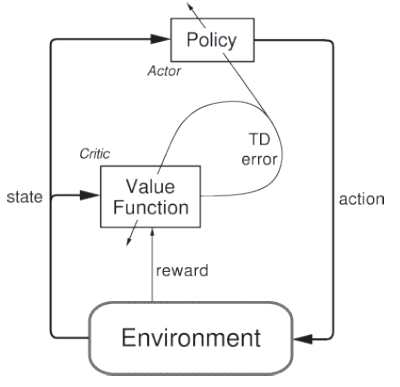
Actor-critic 방법은 별도의 메모리 구조를 갖는 TD(Temporal Difference) 방법이다. 이는 Value function에 독립적인 policy를 갖는 것을 의미한다.
Action을 선택하는 actor와 추정된 Value function critic 으로 구성되고 actor에서 만든 action을 **critic **에서 평가한다.
Action-Value Actor-Critic
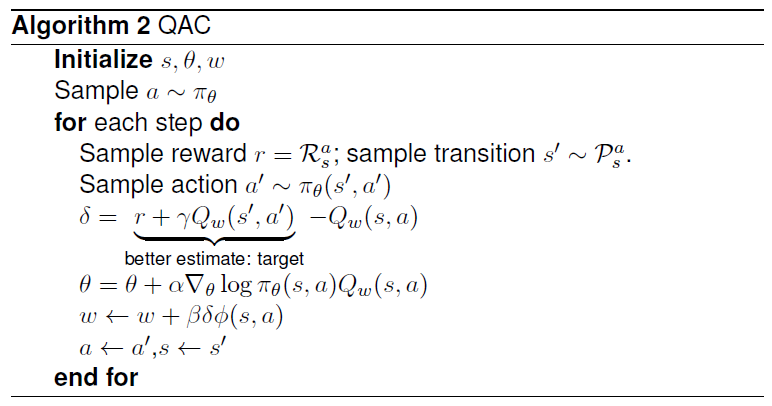
이러한 Action-value critic을 이용한 간단한 알고리즘이 Action-Value Actor-Critic이다.
선형 근사한 value function 를 사용한다.
Actor: Updates by PG
Critic: Updates by linear TD(0)
Bias in Actor-Critic Algorithms
- PG를 근사하는 것은 bias를 만든다.
- 이러한 biased PG는 제대로 된 해를 구하지 못할 수 있다.
value function approximation을 잘 한다면 이러한 bias를 피할 수 있다.
Compatible Function Approximation
Theorem
두 가지 조건이 만족한다면:
-
Value function approximator가 policy와 compatible 하다
-
Value functon 의 가 MSE(Mean-squared Error)를 최소화한다.
Policy Graidient는 정확하다 (exact*)
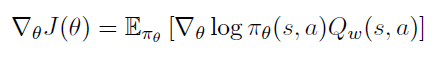
Proof
만약 가 MSE를 최소화할 수 있게 된다면 .w$$w$$\epsilon의 그래이언트는 0이 된다.
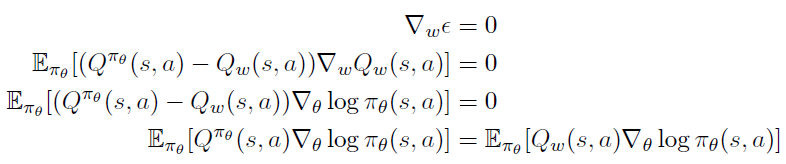
위 조건 2번에 있는 을 대입하여 미분하면 대신 가 들어갈 수 있다.
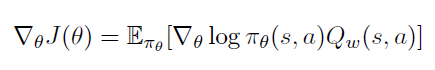
Fisher Information Matrix
Fisher Information Matrix는 log likelihood의 Hessian의 음의 기댓값이다. (the negative expected Hessian of the log likelihood)
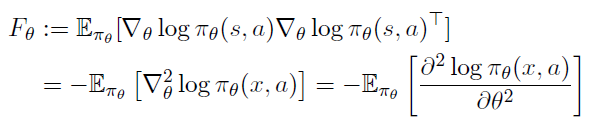
Cramer-Rao Lower Bound Theorem
모든 에 대해 이라고 가정한다면 어떤 unbiased estimator 의 공분산 행렬은 다음을 만족한다.
Newton’s method in optimization
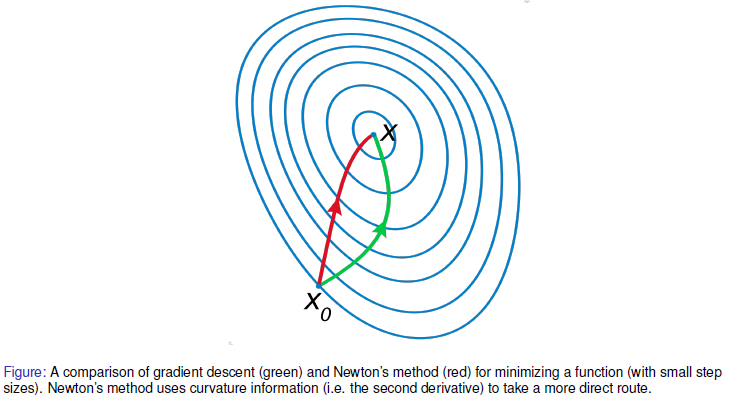
Newton’s method는 2차 미분(the curvature information)을 사용한다.
Natural Policy Gradient
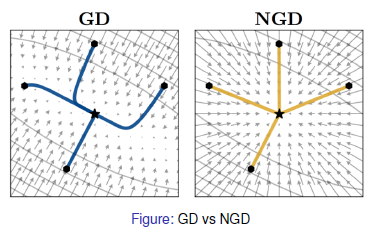
NPG는 피셔 정보행렬을 이용해 기존 gradient와 가깝지만 작고 고정된 양만큼의 방향으로 policy를 업데이트한다.
Natural Actor-Critic
Compatible Function Approximation을 이용해 NPG를 정리할 수 있다. (a Baseline 참고)
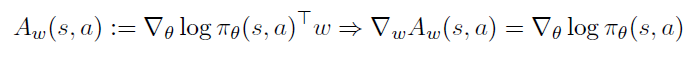
이 때 Advantage fuction 는 a Baseline] 에서 정리한 것 처럼 아래와 같고 이때 Compatible Function Approximation Theorem을 만족하면 PG는 exact하다.
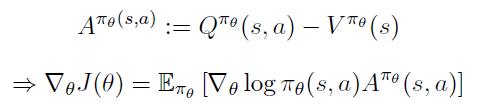

Natural Policy Gradient를 마저 정리하면 이다.
Proof
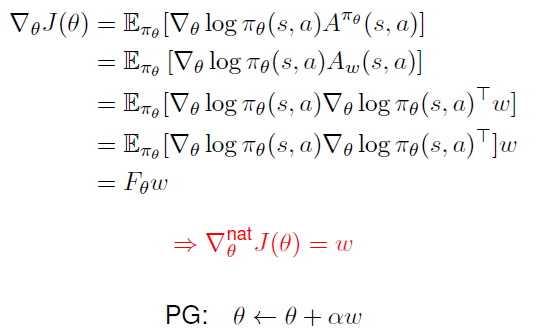
그래서 critic의 의 방향으로 actor의 를 업데이트 한다.
Summary of Policy Gradient Algorithms
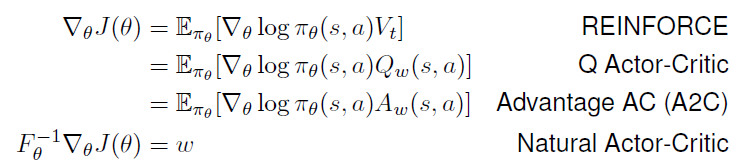
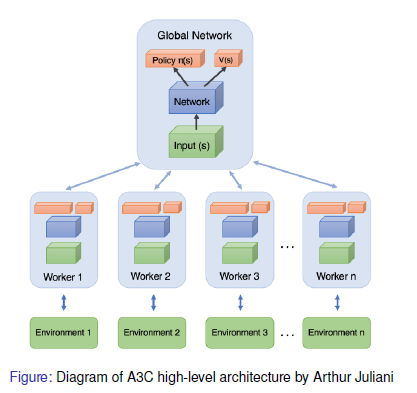
Asynchronous Advantage Actor-Critic Agents (A3C)
아직 스터디에서 A3C를 할 순서는 아니지만 교안에 있으므로 가볍게 짚어보자
Critic (value) loss:
Actor (policy) loss:
여기서 는 엔트로피이다. 하이퍼파라미터 가 엔트로피 정규화 term의 강도를 조절한다.
A3C에는 여러 Worker agent들이 있고 각각이 자신만의 network 변수들을 가진다.
이 Worker agent들은 자신의 환경과 병렬적으로 상호작용한다.
그리고 Global network와 비동기적으로 그래디언트를 업데이트한다.