7. Proximal Policy Optimization Algorithms

논문 Arxiv: https://arxiv.org/abs/1707.06347

놀랍게도 저널이나 학회에 없다…OpenAI라서 그런가

Abstract

PPO는 Policy Gradient (PG)의 하나이지만 data를 sampling하는 대신 stochatic gradient ascent($\simeq$ SGD)를 통해 “surrogate”라는 목적 함수를 최적화한다.

기존의 PG는 data sampling을 할 때마다 한 번씩 gradient를 이동하지만, PPO는 multiple epochs of minibatch update가 가능하다.

Gradient Descent(GD)는 한 epoch당 한 번 minibatch update(=iteration)을 한다. SGD는 epochs * minibatch 만큼 iteration 한다. (Reference)

PPO는 앞서 나온 trust region policy opitmization(TRPO)의 장점 중 일부를 가지지만 훨씬 적용하기 쉽고 널리 사용 가능하다.

Introduction

17년도 당시에는 deep Q-learning, vanila PG, TPRO, natural policy gradient(NPG) 등이 많이 연구되었다. 각자의 단점들이 있지만 TPRO는 data efficiency하고 안정적인 성능을 보였지만, 복잡하고 노이즈에 취약한 단점이 있었다.

본 논문은 TPRO의 장점을 가지면서도 first-order 방식을 사용한 PPO 방식을 제안하였다.

PPO 방식에는 새로운 목적 함수가 도입되었는데 clipped probability ratios를 가지도록 하여 성능의 하한을 가지도록 하였다. 또한, sampled data에 대해 여러 epoch의 최적화를 수행한다. (Stochastic)

Background

Policy Gradient

$$L^{PG}(\theta )=\widehat{{\mathbb{E}}_t}[\log {\pi }_{\theta }(a_t|s_t){\hat{A}}_t]\text{\hspace{1em}(1)}$$

기존의 PG는 다른 action보다 나은 action을 찾는 advantager를 통해 더 나은 reward를 찾도록 하였으나, step size가 작은 경우에는 학습이 너무 느리고 크면 변화 폭이 크다는 단점이 있었다.

Trust Region Methods

TRPO에서는 “surrogate”라고 하는 목적함수가 있다.

$$\underset{\theta }{\max }{\hat{\mathbb{E}}}_t[\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{{\theta }_{old}}(a_t|s_t)}{\hat{A}}_t]\text{\hspace{1em}(2)}$$ $$s.t.\widehat{{\mathbb{E}}_t}[KL[{\pi }_{{\theta }_{old}}(\cdot |s_t),{\pi }_{\theta }(\cdot |s_t)]]\le \delta \text{\hspace{1em}(3)}$$

$\text{subject to}$ 는 KL divergence가 threshold 이하여야 하므로 Policy update의 크기에 대한 제한이다.

여기서 TRPO의 목적함수는 vanilla PG의 Loss function에서 중요샘플링을 통해 바뀐 것이다.

문제는 이 문제가 풀기 어렵다는 것이다. constraint에 대해서는 quadratic approximation이 필요하고, objective에 대해서는 linear approximation이 필요하다. 이후 conjugate gradient algorithm을 통해 근사하게 풀 수 있다.

이 대신 아래와 같이 constraint 대신 penalty 방식으로 식을 바꿀 수 있다.

$$\underset{\theta }{\max }{\hat{\mathbb{E}}}_t[\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{{\theta }_{old}}(a_t|s_t)}{\hat{A}}_t-\beta KL[{\pi }_{{\theta }_{old}}(\cdot |s_t),{\pi }_{\theta }(\cdot |s_t)]]\text{\hspace{1em}(4)}$$

$\max$ 수식에 대해 이러한 페널티는 $\widehat{{\mathbb{E}}_t}$ 대신 state에 대해 KL을 계산하므로 policy의 성능에 대한 lower bound를 만들게 된다.

대신 문제점은 적절한 $\beta$를 찾는 것이 어렵다.

본 논문에서는 적절한 $\beta$를 찾고 SGD를 통해 penalize objective function (3)을 최적화하는 것으로는 충분하지 않음을 보이고 추가적인 수정을 하였다.

Clipped Surrogate Objective

수식 (1)에서 보인 ratio를 the probability ratio $r_t(\theta )=\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{{\theta }_{old}}}$ 으로 둔다. 따라서 $r({\theta }_{old})=1$ 이다.

기존 TRPO에서의 수식 (2)은 constraint없이는 매우 큰 policy update 이다. Why?

그래서 본 논문은 $r_t(\theta )$ 를 최대한 1보다 크게 만드는 방식으로 수식을 수정하였다.

$$L^{CLIP}(\theta )=\widehat{{\mathbb{E}}_t}[\min (r_t(\theta ){\hat{A}}_t,\text{clip}(r_t(\theta ),1-ϵ,1+ϵ){\hat{A}}_t)]\text{\hspace{1em}(5)}$$

$\min$ 안에 있는 첫 번째 인자는 기존 TRPO의 목적함수와 같다. 두 번째 인자는 probability ratio를 hyperparamter $ϵ$으로 clipping 한다. 그리고 이 둘 중의 최소값을 취한다.

이것에 대한 평균을 구함으로써 기존 TRPO 목적함수(unclipped objective)의 하한을 얻게 된다. 이러한 방식은 결국 목적함수를 개선하는 것들은 제외하고, 더 안좋게 만드는 방향을 포함하게 된다.

advantager ${\hat{A}}_t$ 가 양수인 경우에는 평균보다 좋은 action 라는 의미로 $r_t(\theta )$ 가 커지고 이를 $1+ϵ$으로 제한하고, 음수인 경우에는 작아지는 $r_i(\theta )$를 $1-ϵ$ 으로 제한한다.

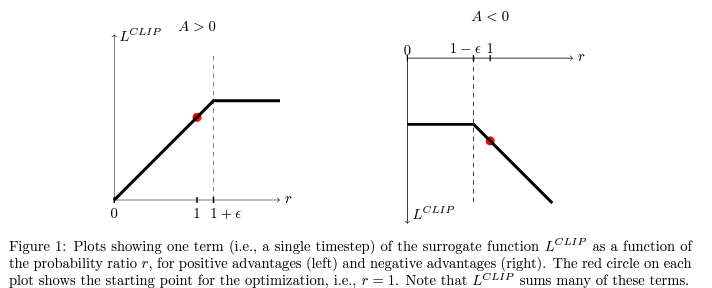
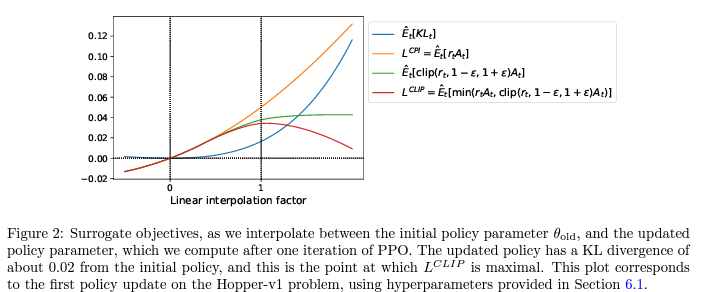
위 Figure 2는 목적함수가 policy update에 따라 어떻게 변하는지 보여주는데, $L^{CLIP}$ (5) 가 기존 TRPO의 $L^{CPI}$ 의 하한이 됨을 알 수 있다

Adaptive KL Penalty Coefficient

이전 섹션에서의 clipped surrogate objective에 더해 식 (4)의 목적함수에 페널티를 가하는 방식도 제안되었다. 이를 통해 매 policy update 마다 원하는 KL divergence 값을 어느정도 도달하도록 만들어준다.

비록 이전의 clipped surrogate objective 방식보다 좋은 성능을 보이지는 않았다.

매 policy update 마다 아래에 대해 수행한다.

• SGD를 통해 KL-penalized objective를 최적화한다.

  $$L^{KLPEN}(\theta )={\hat{\mathbb{E}}}_t[\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{{\theta }_{old}}(a_t|s_t)}{\hat{A}}_t-\beta KL[{\pi }_{{\theta }_{old}}(\cdot |s_t),{\pi }_{\theta }(\cdot |s_t)]]\text{\hspace{1em}(6)}$$

• $d=\widehat{{\mathbb{E}}_t}[KL[{\pi }_{{\theta }_{old}}(\cdot |s_t),{\pi }_{\theta }(\cdot |s_t)]]$ 를 계산한다.

  • $\text{if}d<d_{targ},\beta \leftarrow \beta /2$
  • $\text{if}d>d_{targ}\times 1.5,\beta \leftarrow \beta \times 2$

결국 이 방식은 기존 TRPO 최적화 문제를 페널티 방식으로 바꾼 것에서 $\beta$를 적절히 찾는 방식을 제안한 것으로 보인다.

1.5와 2 연산은 heuristic하게 정해진 것이나 이 변수들에 크게 민감하지 않고 $\beta$의 초기값도 바로 변하기 때문에 값 설정에 큰 부담이 없다.

Algorithm

본 논문의 큰 장점 중 하나는 기존 vanila policy gradient에서 몇가지의 코드 수정으로 쉽게 적용이 가능하다는 것이다.

하나는 $L^{PG}$ 대신 $L^{CLIP}$ 또는 $L^{KLPEN}$ 을 적용하는 것이고 다른 하나는 여러 step의 SGD를 수행하도록 바꿔주면 된다.

PPO는 고정된 궤적의 요소를 사용한다. 매 반복마다 각 N 개의 병렬적인 actor들이 T 시간만큼의 데이터를 수집한다. 그리고 surrogate loss를 NT 개의 data로 구성하여 K epoch만큼 minibatch SGD 방식으로 최적화한다.

variance-reduced advantage-function estimator를 계산하기 위해 학습된 state-value function $V(s)$ 를 사용한다.

policy function과 value function 간의 parameter를 공유하는 NN 구조에서 PPO는 loss function에서 policy surrogate와 value function error term이 결합된 것을 사용해야 한다.

선행 연구에서 entropy bonus를 추가한 방식도 더해 아래와 같이 목적 함수를 구성함.

$$L_t^{CLIP+VF+S}(\theta )=\widehat{{\mathbb{E}}_t}[L_t^{CLIP}(\theta )-c_1{L}_t^{VF}(\theta )+c_{2}S[{\pi }_{\theta }](s_t)]\text{\hspace{1em}(7)}$$

$c1,c2$는 계수이고, $S$가 entorpy bonus에 해당한다. $L_t^{VF}$는 squared-error loss $(V_{\theta }(s_t)-V_t^{targ}{)}^2$이다.

선행 연구에서 RNN에 적합하고 T 시간 만큼 policy를 수행하여 데이터를 수집하는 방식을 적용하였는데, 이 때의 advantage estimator는 아래와 같다.

$${\hat{A}}_t=-V(s_t)+r_t+\gamma r_{t+1}+\cdots +{\gamma }^{T-t+1}{r}_{T-1}+{\gamma }^{T-t}V(s_T)\text{\hspace{1em}(8)}$$

step이 작으면 편향이 크고 분산이 낮지만, step이 큰 경우 편향은 작지만 분산이 커진다. 따라서 Generalized Advnatage Estimation 방식을 사용하였다.

위 수식 (7)을 일반화하여 $\lambda =1$로 두고 아래의 truncated version of generalized advantage estimation을 사용하였다.

$$\begin{array}{rl}& {\hat{A}}_t={\delta }_t+(\gamma \lambda ){\delta }_{t+1}+\cdots +(\gamma \lambda {)}^{T-t+1}{\delta }_{T-1}\\ & \text{where}{\delta }_t=r_t+\gamma V(s_{t+1})-V(s_t)\end{array}\text{\hspace{1em}(9)(10)}$$

논문 요약 끝!

결국 PPO는 현재와 이전 policy의 비율과 clipping 방식을 통해 학습의 안정성을 높이면서 너무 큰 policy update를 피하도록 하였다.

References

• Original paper: https://arxiv.org/abs/1707.06347
• Huggingface Deep RL doc: https://huggingface.co/learn/deep-rl-course/unit8/introduction
• “Towards Delivering a Coherent Self-Contained Explanation of Proximal Policy Optimization” by Daniel Bick : https://fse.studenttheses.ub.rug.nl/25709/1/mAI_2021_BickD.pdf
• PPO 논문 리뷰: https://www.youtube.com/watch?v=L-QYXtJmXrc