Transformers from Scratch

LLM 을 공부하기 이전에 Attention 메커니즘과 Transformer 구조를 공부해봐야겠다고 생각하여 모아놓은 여러 자료들 중에 하나하나 세세히 설명해주는 포스트 먼저 읽어보았다.

영어로 써있는데다가 수학적인 내용을 말로 풀어져 있다보니 읽는데 꽤 시간이 걸렸다.

Quote

Transformers from Scratch

One-hot encoding

어휘를 수학으로 표현하기 위해 사용하는 방법이다. 예를 들어, files=1, find=2, my=3 로 단어에 숫자를 할당한다면 “Find my files” 라는 문장은 [2, 3, 1] 의 벡터로 표현할 수 있을 것이다.

이 대신에 각 단어를 하나의 요소만 1을 가지고 단어의 갯수 $N$ 의 크기를 가지는 unit vector 로도 표현할 수 있다. 이를 one-hot encoding 이라고 한다.

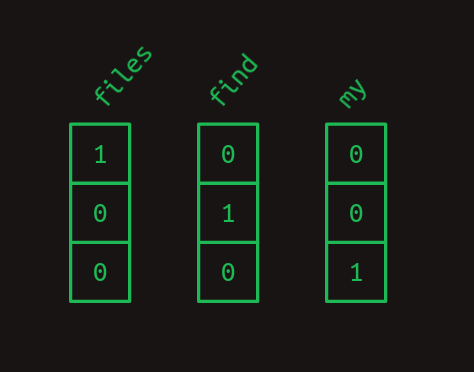
그러면 아까 “Find my files” 라는 문장은 matrix 로 표현가능해진다.

First-order sequence model

이제 Markov chain 을 통해 일련의 유사한 문장들을 표현해보고자 한다.

예를 들어, Show me my directories please. Show me my files please. Show me my photos please.

와 같은 문장들의 경우 고려되는 어휘의 크기는 7이 되었다. ({directories, files, me, my, photos, please, show})

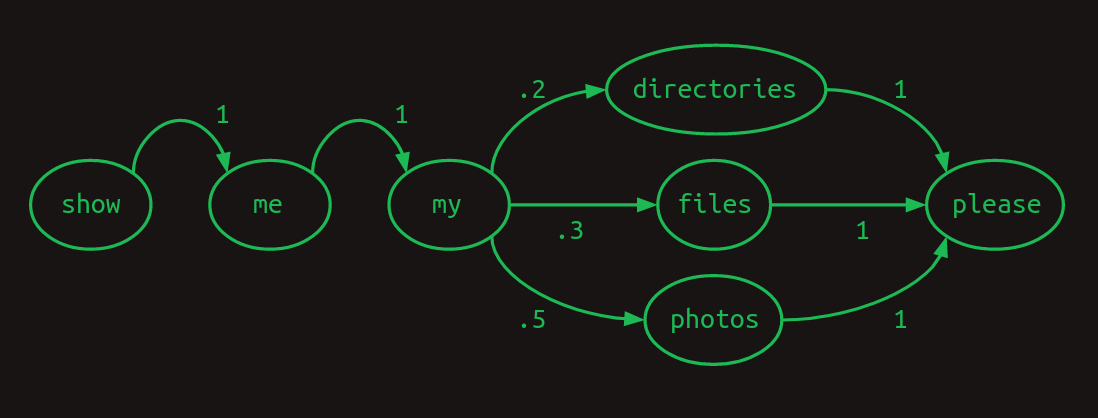
물론 각각의 transition 의 확률은 예를 든 것이다. 다음 단어가 나타날 확률은 전적으로 이전 단어에 달려 있으므로 Markov property 를 만족하고, transition 의 확률의 합이 1 이므로 이를 Markov chain 이라고 할 수 있다.

이러한 transition 의 확률을 행렬로 표현하는 것이 transition matrix 이다.

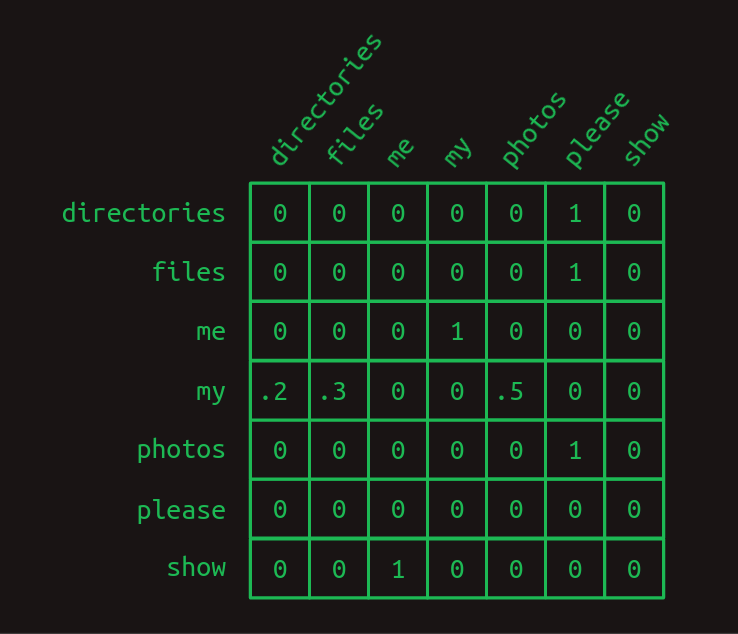
column 에 있는 단어 다음에 올 단어의 확률이 각 row 에 나타나 있고, 이를 one-hot vector 와 transition matrix 를 행렬곱(matrix multiplication) 하면 간단히 추출해낼 수 있다.

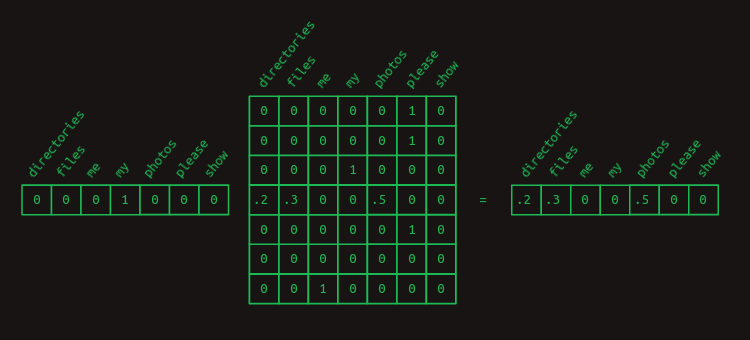
Second-order sequence model

위에서 다룬 first-order sequence model 은 하나의 단어 다음 올 단어만 예측하면 되어서 비교적 단순했지만, 이러한 단어의 조합이 복잡해질 수록 문제는 어려워진다.

이제 유사한 문장이지만 단어의 연속이 두 차례에 걸쳐 얽혀 있는 경우를 살펴보자. Check whether the battery ran down please Check whether the program ran please

이를 Markov chain 으로 예를 들면 아래 이미지와 같다. (아직 first-order 이다.)

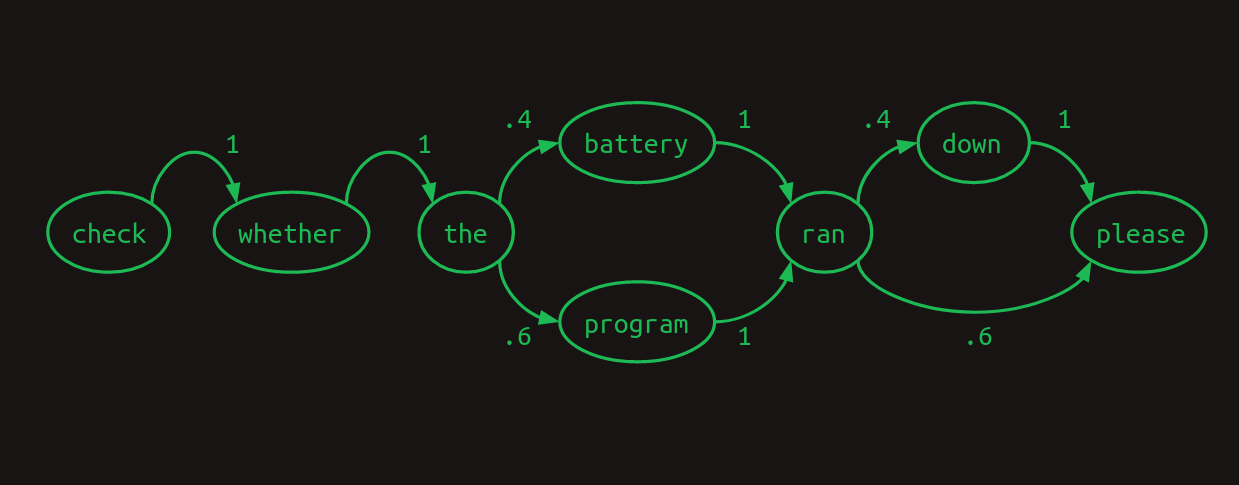
우리가 원하는 조합은 정해져 있기에 battery ran 뒤에는 반드시 down 이 와야 하고, program ran 뒤에는 please 가 와야 한다.

즉, 앞서 1차 모델과 달리 ran 만으로는 뒤에 올 단어를 확정적으로 알 수 없고 두 단어를 알아야 하게 된다.

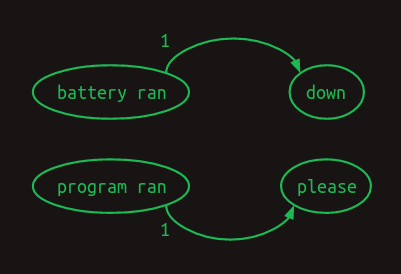
그렇다면 이를 표현하기 위한 transition matrix 는 각 단어의 모든 조합에 대해 row 를 가져야 하고 $N$ 개의 어휘를 가지고 있다면 row 의 크기가 $N^2$ 가 됨을 의미한다.

당연하게도 예시에서 든 문장을 처리하기 위해 first-order transition matrix 를 사용하는 것 보다 second-order transition matrix 가 더 정확하고 확실하게 다음 단어를 예측해낼 수 있다.

그러나 이 예시에서는 단순히 연속한 두 단어로 해결이 되었지만, 문맥을 알기 위해 더 앞서서까지 알아내야 한다면 어떨까?

Second-order sequence model with skips

이제 이런 예시를 살펴보자 Check the program log and find out whether it ran please. Check the battery log and find out whether it ran down please.

이 예시에서는 ran 뒤에 올 단어를 알아내기 위해 저 앞까지 가보아야 한다. (program 인지 battery 인지)

단순하게 생각해보았을 때 이는 eight-order transition matrix 가 되고, $N^8$ 개의 row 를 가지는 행렬이 된다.

이러한 방식 대신에 가장 가까운 단어와 다른 단어들의 조합으로 second-order model 을 만들어 낸다.

즉, ran 과 다른 단어를 조합하고 이들의 확률로 다음 단어가 down 일지, please 일지 예측하는 것이다.

이렇게 하면 long range dependencies 를 효과적으로 해결할 수 있다.

각 확률을 화살표의 굵기로 도시화 하면 아래와 같을 것이다.

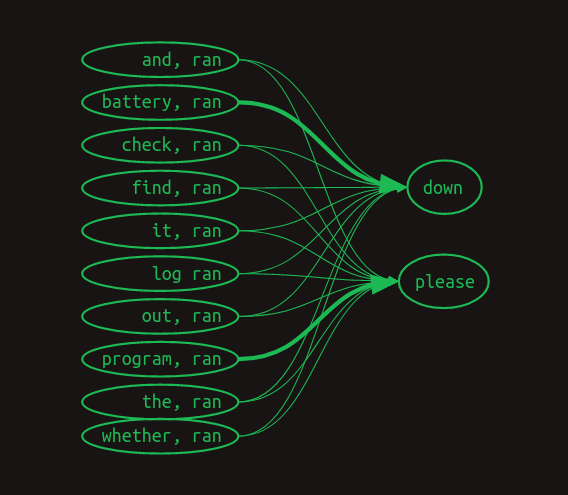
Markov chain 방식은 더이상 아니지만 위의 도시화를 transition matrix 로 표현해보자.

보다시피 ran 뒤에 올 단어를 예측하기 위해 다른 단어들과 ran 의 조합에 따른 확률이 표현되었고 down 과 please 외의 단어들은 확률이 0이어서 비어있게 표현되었다.

그리고 앞서 Markov chain 에서의 transition matrix 와 달리, 다음 단어를 알기 위해서는 모든 row 를 살펴보아야 하고 column 요소의 합 또한 더이상 1이 아니다.

그래서 이제는 확률의 의미가 아닌 vote 의 의미가 되고 이를 합하거나 비교함으로써 다음 단어를 예측한다.

예를 들어, Check the program log and find out whether it ran 은 down 에서는 4표, please 에서는 5표이고 나머지 모든 단어들은 0표가 될 것이고, Check the battery log and find out whether it ran 은 down 에서 5표, please 에서 4표고 나머지는 0표일 것이다. 따라서 가장 높은 표를 갖는 단어를 선택해서 long range dependencies 에도 불구하고 올바른 다음 단어를 예측해낼 수 있다.

Masking

아주 기초적인 예측 방법을 살펴보았지만, 4표와 5표 차이는 매우 작기 때문에 강건한 예측 모델이라고 하기는 어려울 것이다.

더 크고 noisy 한 모델에서는 이정도 작은 차이에서는 모델이 길을 잃기 쉽다.

그래서 예측을 더 잘하기 위해서 불필요한 정보의 feature votes 를 모두 없앨 것이다.

1과 0으로 이루어진 vector 를 transition matrix 에 곱하면 불필요한 feature 들을 모두 없앨 수 있다는 것을 알고 있으므로, 우리가 예측하고자 하는 단어의 직전 단어와 그 전에 나타났던 단어들만 사용하는 feature selection vector 를 사용한다.

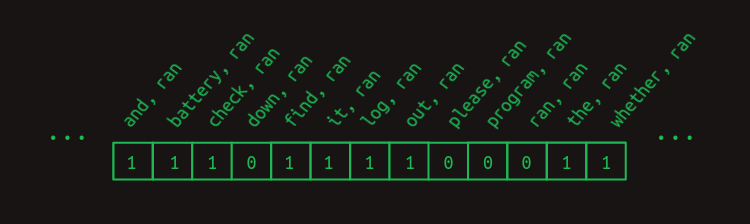
보다시피 ran 전에 나오지 않았던 down, please, program, ran 은 조합에서 고려하지 않는 것이다. (feature 로 작용할 단어로써 무의미한 단어들이다.)

그리고 여기에 mask 를 더하여 주목하고자 하는 조합만 얻어낼 수 있다.

이를 transition matrix 로 표현해보면 battery 와 program 외에 모든 요소들은 0이 되어 다음 단어의 예측을 확정적으로 해낼 수 있다.

이 masking 을 선택하는 과정을 attention 이라고 한다. (ref. Attention is All You Need)

이제 Transformer 구조를 살펴보기 위한 기본적인 요소들을 모두 다루었다.

Attention as matrix multiplication

앞서 mask vector 를 찾는 과정을 임의적인 예시로 들었지만 이제는 transformer 가 어떻게 필요한 mask vector 를 찾는지 살펴보고자 한다.

one-hot vector 와 transition matrix 의 곱으로 원하는 row 를 얻어냈듯이, 아래와 같이 query 와 keys 를 통해 feature-specific mask vector 를 찾는다.

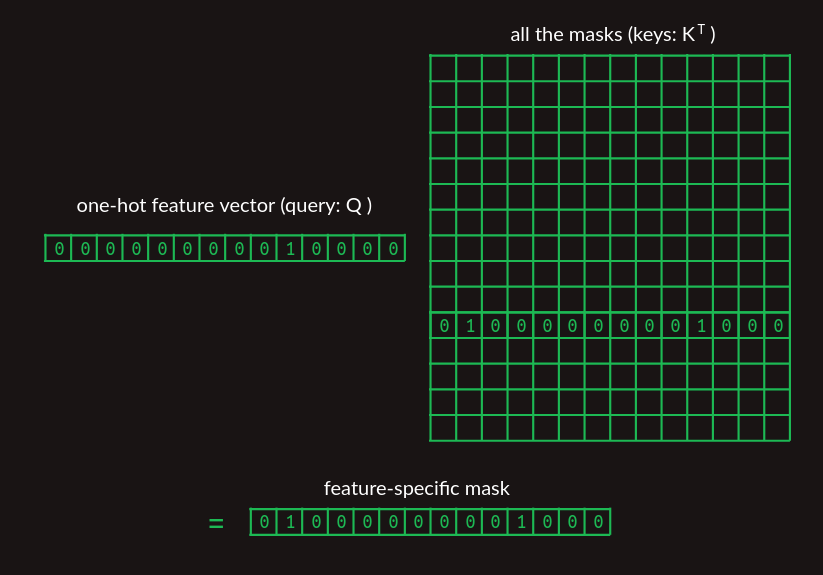
드디어 논문에 담겨 있는 수식의 일부분을 들여다 보게 되었다.

$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V$$

이 mask lookup 이 attention 수식의 $Q{K}^T$ 부분을 의미한다.

Second-order sequence model as matrix multiplication

Attention 과정으로 가장 최근의 단어와 그 이전 단어의 조합을 얻어냈지만, 이를 feature 로 변환해주어야 한다. Attention masking 은 각 요소들을 얻게 해줄 뿐, word pair feature 를 만들어주는 것은 아니다.

이를 위해, single layer fully connected neural network 를 사용할 수 있다

battery, program, ran 만을 이용해 아주 간단한 예시를 몇 가지 이미지들로 나타내보자.

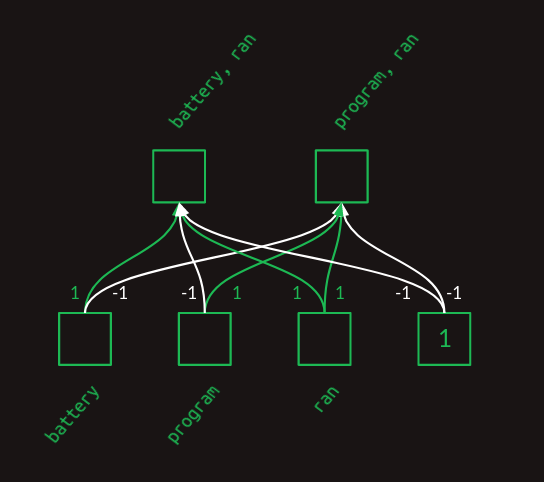
이 layer 도표에서 각 가중치를 통해 단어의 조합에서 각 단어의 존재 유무를 표현했음을 알 수 있다.

이제 이러한 행렬을 matrix multiplication 으로 feature vector 와 곱하면 word pair vector 를 얻어낼 수 있다.

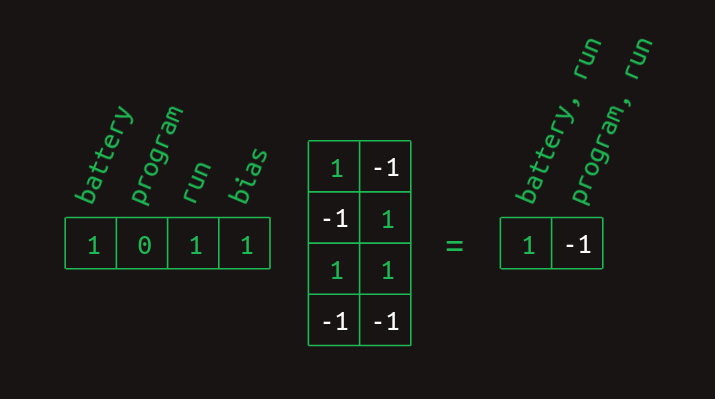
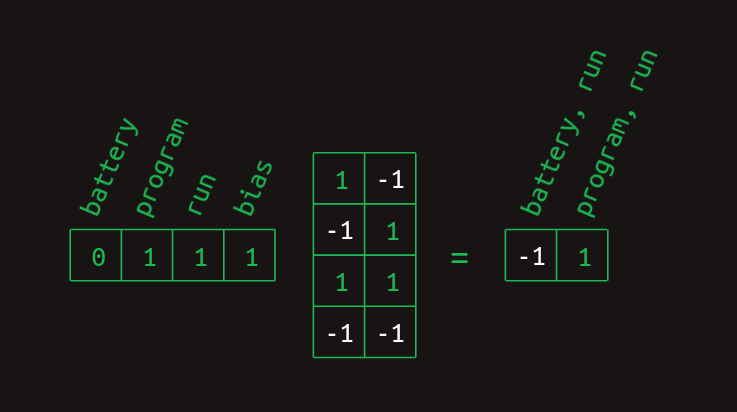
여기에 ReLU 를 곱연산 하여 존재하는 경우 1로, 없는 경우 0으로 표현되는 vector 로 변환해준다.

여태 살펴본 기초 개념들의 모든 과정을 matrix multiplication 으로 바꾸어주었고 Masking 에서 살펴본 과정처럼 masked feature vector 가 얻어져서 transition matrix multiplication 을 하면 다음 단어를 얻어낸다.

이를 요약해보면 feature creation matrix multiplication ReLU nonlinearity transition matrix multiplication 이 된다.

이러한 과정이 attention 이후 진행되는 feedforward 과정이다. (논문의 수식 (2))

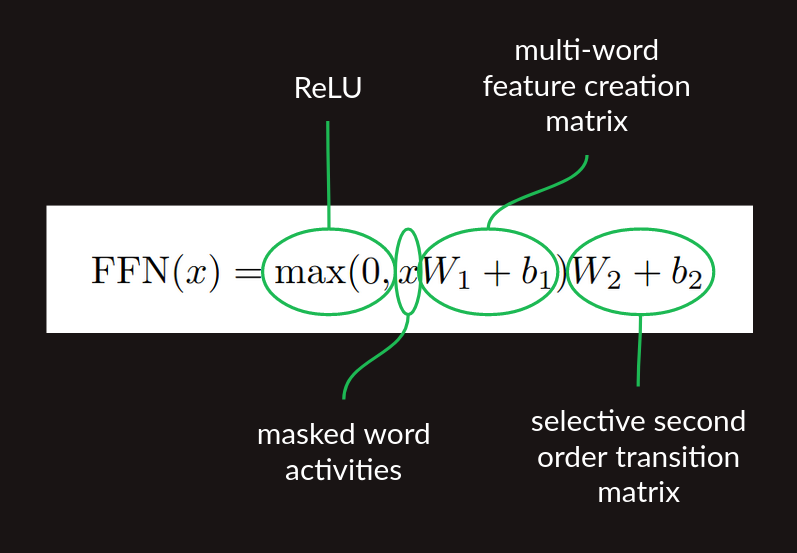
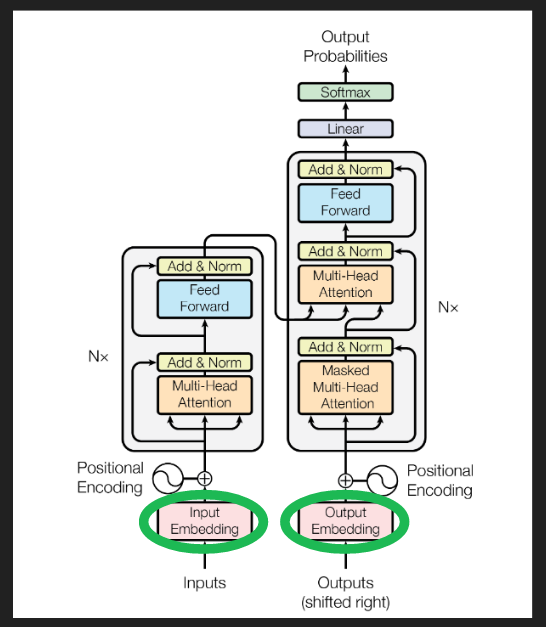
이 과정이 transformer 구조에서 Feed Forward 블럭에 해당한다.

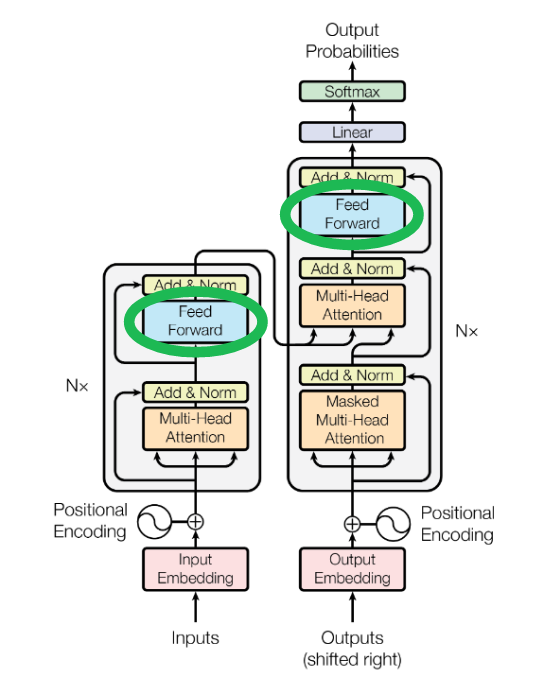
Sequence completion

지금까지는 다음 단어를 예측하는 것에 대해서만 다루었다. Decoder 가 긴 sequence 를 생성하도록 하려면 첫 번째로 prompt 가 필요하다.

prompt 는 transformer 시작과 나머지 sequence 를 구축할 수 있도록 맥락를 제공하는 몇 가지 예제 텍스트이고, 위 이미지의 오른쪽에 있는 “Outputs(shifted right)” decoder에 입력된다.

Decoder 가 시작하기 위한 부분적인 sequence 를 얻으면 forward pass (위 쪽 방향으로 진행) 를 사용한다. 최종 결과는 단어의 예측 확률 분포 집합으로, sequence 의 각 위치에 대해 하나의 확률 분포가 생성된다. 각 위치에서 분포는 그 어휘의 다음 단어에 대한 예측 확률을 의미한다.

Sequence 에서 이미 설정된 각 단어에 대한 예측 확률은 이미 정해져 있으므로 고려하지않고, prompt 가 끝난 후 다음 단어에 대한 예측 확률에 관심을 갖는다. 그 단어를 선택하는 방법에는 여러 가지가 있지만, 가장 간단한 방법은 가장 높은 확률을 가진 단어를 선택하는 ‘greedy’ 방식이다.

그런 다음 새로운 다음 단어가 sequence 에 추가되고 디코더 하단의 ‘Outputs’ 에 대입되며, 이 과정을 계속 반복한다.

Transformer 구조에서 아직 다루지 않은 Masked Multi-Head Attention 은 이후에 살펴볼 예정.

Embeddings

언어를 one-hot vector 로 표현하기 때문에, 각 단어를 표현하는 vector 가 있다. 만약 $N$ 개의 어휘는 $N$ 차원의 공간에서의 vector 들일 것이다.

embedding 에서는 이러한 단어들을 저차원 공간으로 projection 하는 것이다.

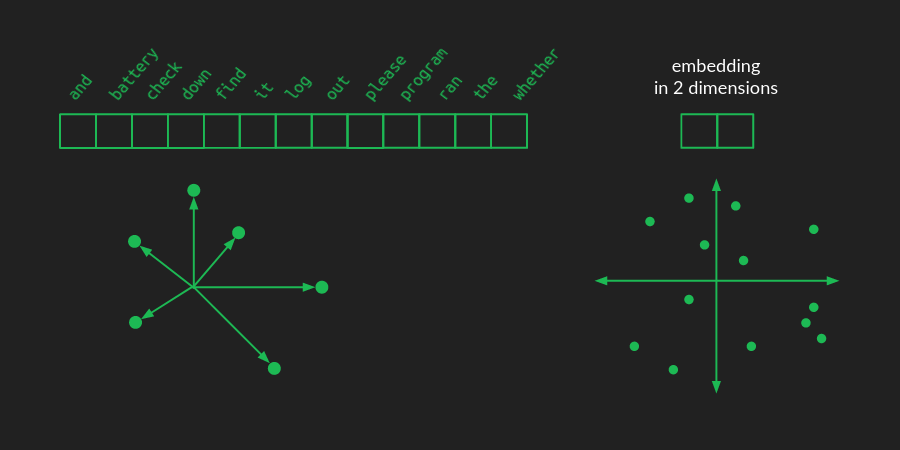
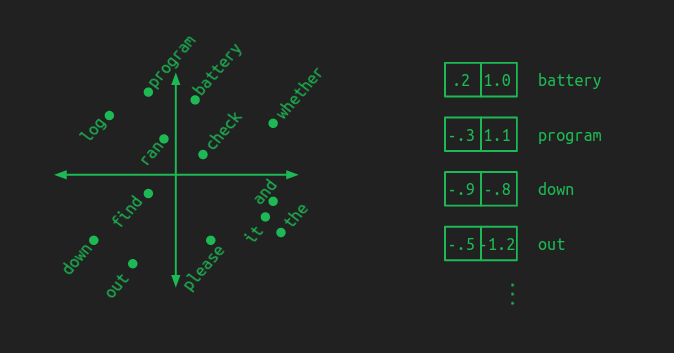
위 그림처럼 2차원 공간으로 표현한 예시를 생각해보면, 각 단어들이 $(x,y)$ 좌표로 표현될 것이다.

그리고 이러한 embedding group 은 유사한 의미들끼리 비슷한 위치에 놓이게 된다. 이로서 한 단어를 학습하므로써 자연스레 유사한 단어들도 학습되어 학습 데이터를 적게 사용할 수 있다.

하지만 embedded space 의 차원이 작을 수록 원래 단어의 대한 정보들이 적어진다. 따라서 연산의 부담과 모델의 정확도 사이에서 적절한 크기의 embedded space 를 선택해야 한다.

단어의 projection 을 위해 one-hot vector 와 embedding projection matrix 를 행렬곱한다. one-hot matrix 가 1 개의 row 와 $N$ 개의 column 을 가진다면, embedding projection matrix 는 $M$ (차원) 개의 column 을 가지고 $N$ 개의 row 를 가질 것이다.

예를 들어, 위 그림처럼 2차원 공간에 투영하는 경우에는 $N\times 2$ 크기의 행렬이다.

비슷한 단어들을 함께 그룹화하고, 적절히 분산할 수 있는 projection matrix 를 찾기 위해 학습 과정에서 같이 학습시킬 수 있다.

Positional encoding

embedding 으로 표현한 단어에는 아직 위치에 대한 정보는 포함되지 않았다. 위치 정보를 적용하는 방식에는 여러가지가 있지만 original transformer 논문에서는 원형의 움직이는 방식을 사용하였다.

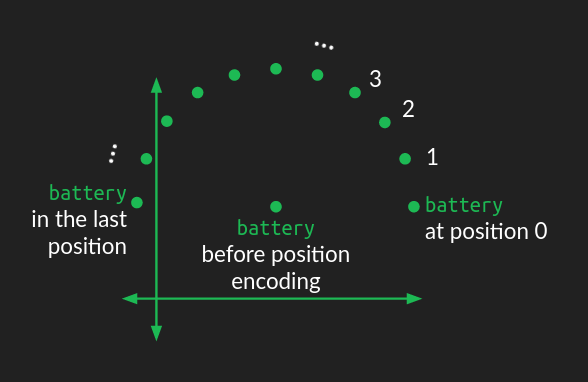
단어의 sequence 에서의 순서에 따라 다른 각도로 이동하면서 원형의 패턴을 가지게 된다. 고차원의 embedding 공간에서는 단순히 원형으로 표현하는 것은 불가능하기 때문에 다른 각속도로 이동하여 표현된다.

이 내용에 대해서는 제대로 이해가 되지는 않지만, 개략적으로 위치를 찾아주는 부분으로 이해하였다. Transformer 구조에서는 “Positional Encoding 블록에 해당한다.

De-embeddings

모든 과정이 지나고나서 embedding 한 단어는 다시 원래의 어휘로 돌아오는 과정이 필요하다. 이를 de-embedding 이라고 한다.

Embeddings 에서 표현한 반대로 열과 행의 크기가 바뀐 (=transpose) 행렬을 곱해주면 된다.

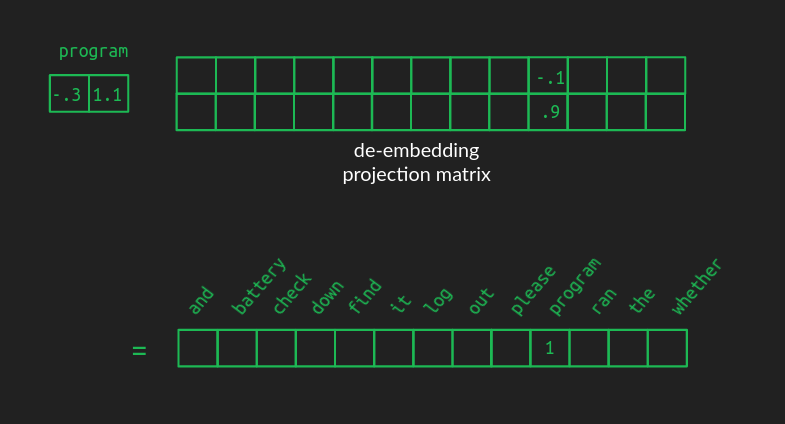
다만, 문제는 저차원에서 고차원으로 복원하는 것이기 때문에 이전처럼 다른 어휘들도 0이 아닌 값을 가지게 된다. 이해를 위해 아래 그림을 참조하자.

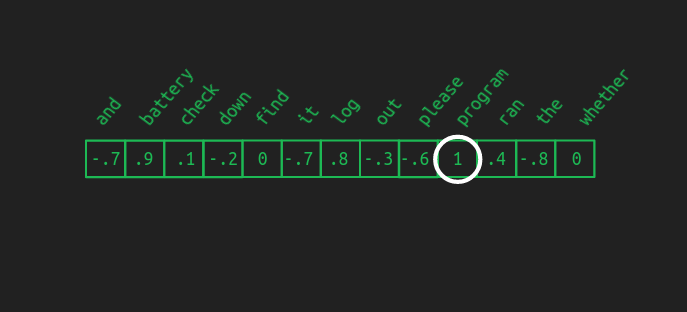
따라서 가장 높은 단어를 선택하기 위해 greedy 한 방식인 $\arg \max$ 를 사용한다.

Softmax

argmax 는 단 하나의 최대값을 얻게 해주므로, 확률분포를 얻을 수 있는 softmax 를 사용한다. 이번에 알게 된 것인데, 보통의 neural network 에서 마지막 활성함수로 잘 사용된다고 한다.

$$\text{softmax}(\mathbf{x})=\frac{e_i^x}{{\sum }_{j=1}^K{e}_j^x}\forall i=1,\dots ,K$$

확률분포를 얻게 해주는 장점 외에도 argmax 와 거의 유사한 결과를 주면서도 미분 가능하다.

Transformer 구조도에서 가장 마지막에 위치하고 있다.

Multi-head attention

$N$ 은 어휘의 크기, $n$ 은 최대 sequence 길이 그리고 $d_{m}odel$ 은 embedding 공간의 dimension 이라고 하자.(논문에서는 512)

그렇다면 one-hot 으로 표현되는 $N$ 개의 단어들이 $n$ 개만큼 나열되므로 input matrix 의 크기는 $n\times N$ 이 될 것이다.

이를 embedding 공간으로 projection 하면 $n\times d_{m}odel$ 크기의 행렬이 embedded word sequence 가 된다.

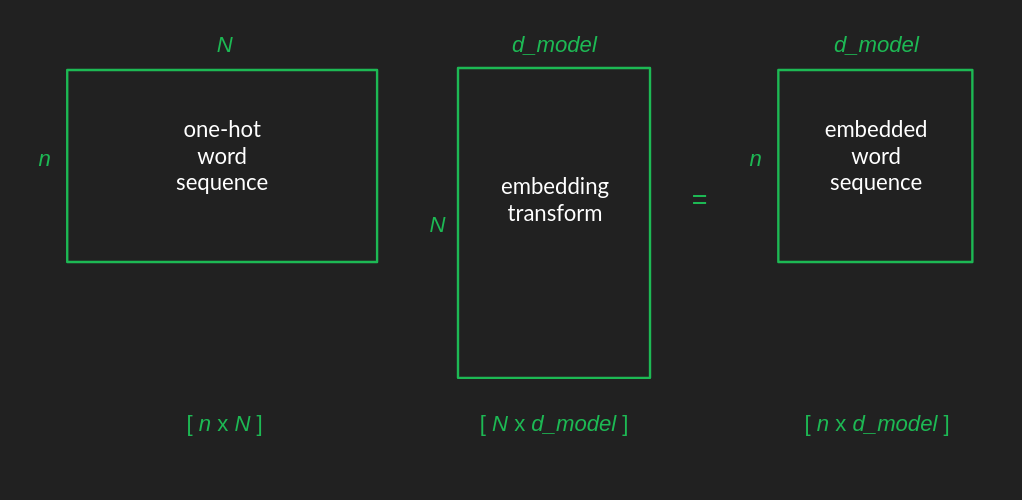
Position encoding 은 multiplication 이 아니라 concatenate 되는 방식이므로 dimension 을 변화시키진 않는다. 이후 attention layers 를 지난 후에는 de-embedding 을 통해 원래의 크기로 돌아와 sequence 안의 각 단어들의 위치를 가진 확률 분포를 만들게 된다.

why we need more than one attention head

앞서 다뤄보았던 대로 단어들이 attention mechanism 에 들어갈 때 더이상 one-hot vector 가 아닌 dense 한 embedded vector 로 표현되어 있다. 따라서 결과도 또한 $[0,1]$ 사이에 존재하게 되는데 softmax 를 사용하게 되면 미분가능한 argmax 와 유사한 확률 분포를 얻어 가장 큰 요소에 집중하게 된다.

우리가 다음 단어들을 예측할 때 여러 개의 좋은 후보군들을 유지하는 것이 더 나을수도 있는데, softmax 는 이러한 가능성을 없애버린다.

여기서 사용한 방법은 여러 개의 다른 attention 혹은 heads 가 작동하는 것이다.

이로써, transformer 가 여러 개의 이전 단어들을 동시에 고려하여 다음을 예측한다.

연산량이 커지는 부담은 저차원의 embedding 공간을 사용하여 matrix 크기를 낮춰 어느 정도 해결할 수 있다.

$d_k$ 를 embedding 공간에서 keys 와 queries 의 크기라고 하고 $d_v$ 를 value 의 크기라고 하자. 논문에서는 둘 다 같은 64로 설정되었다. $h$ 는 head 의 수 이다. 논문에서는 8로 되어 있다.

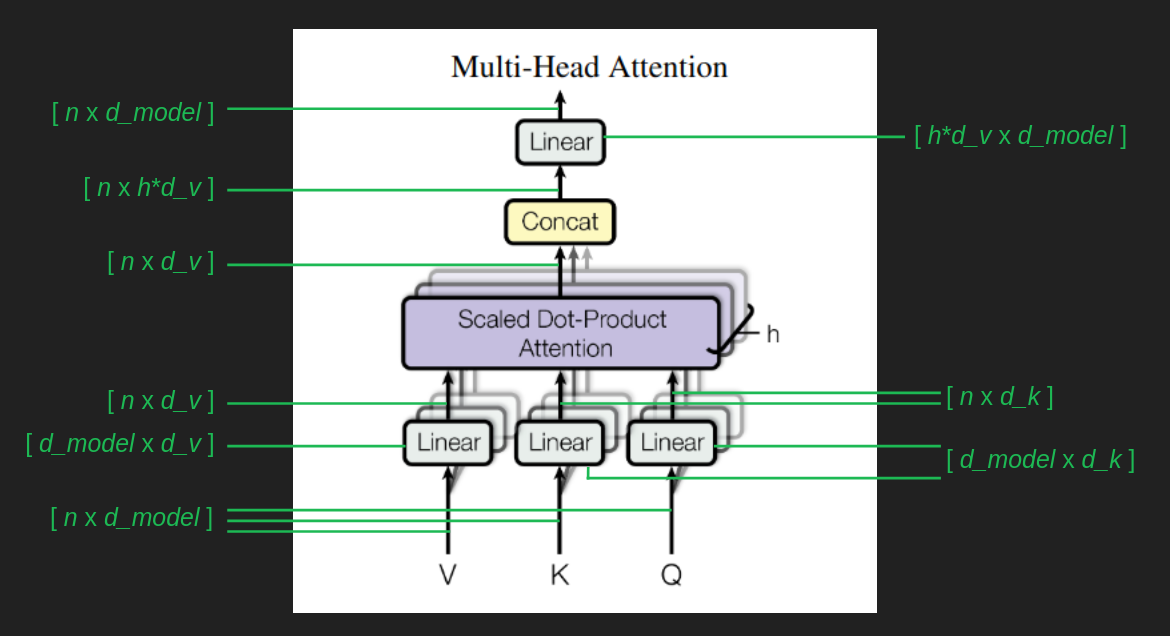
위 그림을 통해 이 과정을 자세히 이해해보자. Linear 로 쓰여있는 블럭은 $W_v,W_q,W_k$ 로 표현할 수 있는 matrix 이다. 이는 이전 과정에서 embedded matrix 의 dimension 을 바꿔준다.

바뀐 행렬 중 value 행렬은 $V$, query 행렬은 $Q$ 그리고 key 행렬은 $K$ 가 된다. 그림을 자세히 보면 여러 개의 Linear 블록이 있음을 알 수 있다. $h$ 개의 attention head 마다 고유의 $W_v,W_q,W_k$ 를 가지고, 어떤 부분에 집중할 지에 따라 head 들 마다 다른 행렬을 가진다.

결과로 나온 행렬들은 다른 값을 지니고 있는 $h$ 개의 행렬들이므로, 이를 concatenate 하여 $[n\times h\ast d_v]$ 크기의 행렬로 구성한다. (Concat)

처음 들어올 때와 같은 dimension 을 유지하기 위해 multiplication 을 해주면 $[n\times d_{m}odel]$ 의 행렬로 결과물이 나오게 된다.

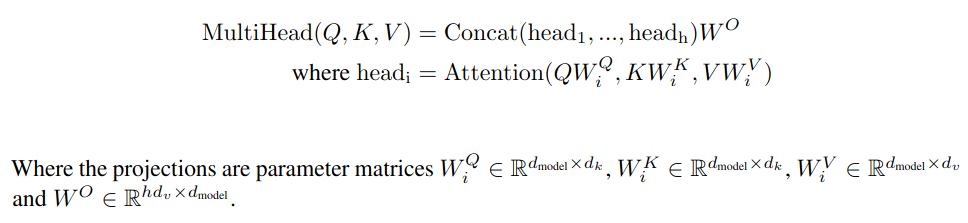
Single head attention revisited

Attention as matrix multiplication 에서 간략히 이해한 내용은 단어 (query) 에 대해 모든 masking vector (keys) 를 곱해 집중할 필요가 없는 단어들을 제외할 수 있었다. (matmul w/ values)

embedding 이 이루어진 $Q,K,V$ 는 단 하나의 단어 대신에 유사한 단어들의 집합이기 때문에 query 또한 단어 집합으로 이해해야 한다. 따라서 각 attention head 는 단어 집합 간의 mapping 으로 이해할 수 있다.

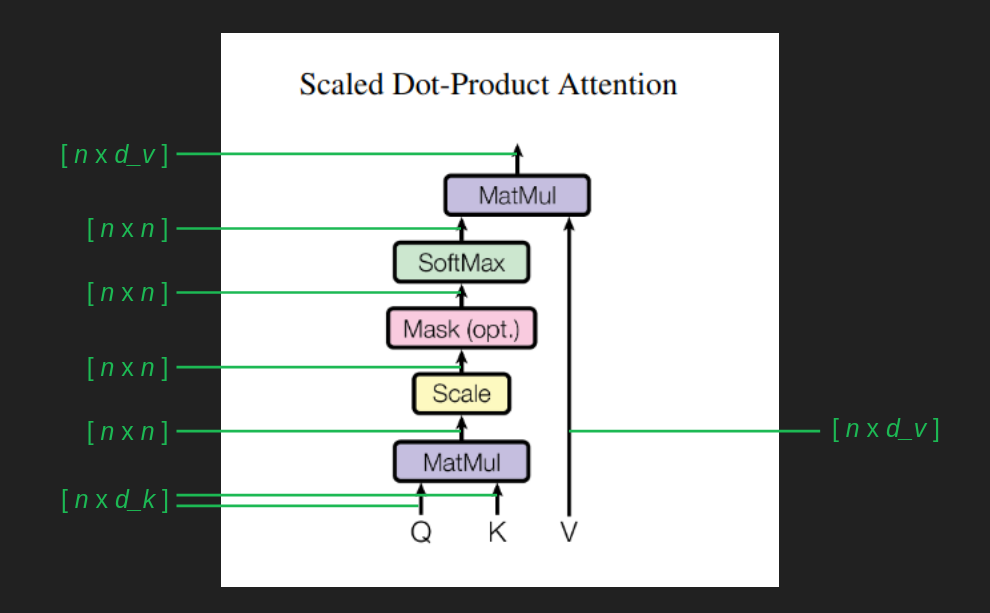
위 그림은 그러한 과정을 dimension 을 고려하여 표현하였다. $Q{K}^T$ 로 계산된 결과는 $[n\times n]$ 크기를 갖게 되는데 이를 $\sqrt{d_k}$ 로 나누어 값이 너무 커지는 것을 방지하고, 역전파 과정을 쉽게 해준다.

softmax 를 지나 나오는 확률 분포는 sequence 의 각 요소가 문맥을 고려해서 다음 단어를 예측하기 위해 어떤 단어들을 보아야 하는지 나타내게 된다.

그리고 이를 $V$ 와 곱하여 필터링이 이루어지게 된다.

$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V$$

위 수식은 사실 가장 최근 단어뿐만 아니라 input sequence 의 모든 요소, 즉 문장의 모든 단어에 대한 attention 을 계산한다는 점을 유의해야 한다.

다음 단어는 이미 예측하여 정해져 있지만, 이전 단어와 미래 단어에 대한 관심도가 가장 최근의 단어에 대한 관심도에 영향을 미칠 수 있기 때문이다. 다만 마지막에 sequence 의 모든 위치에 대한 단어 확률을 계산할 때 대부분을 버리고 다음 단어에만 집중할 뿐이다.

앞서 설명되지 않았지만 그림에 있는 Mask 블록은 적어도 이 sequence 작업에서는 다음을 예측할 수 없다는 제약을 적용하는 의미이다. (single head 이므로)

현재 위치 이후의 모든 단어에 대한 주의력을 음의 무한대로 임의적으로 설정하여, 미래 단어에서 이상한 결과가 나오는 것을 방지한다.

Skip connection

Transformer 의 중요한 부분들은 다 살펴보았고 이제부터는 잘 작동하기 위해 필요한 디테일한 부분들에 대해 이해해보자.

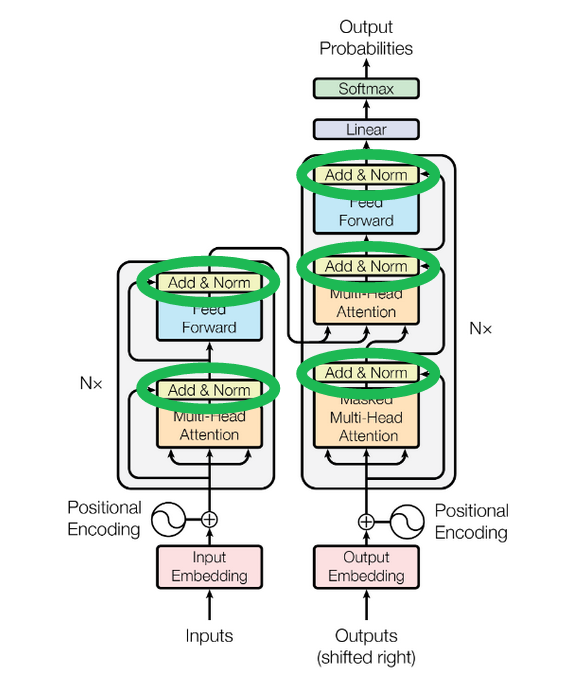
위 그림에서 보이는 Add & Norm 블록이 skip connection 역할을 하는 부분이다.

Multi-Head Attention 이나 Feed Forward 에 들어가는 input 이 복사되어 output 에 합쳐진다.

Skip connection 은 두 가지 목적을 위해 이루어진다.

첫 번째는, 경사하강 (gradient) 를 smooth 하게 유지해주어 역전파 과정을 좋게 만들어준다. Attention 은 앞서 얘기한대로 필터로 작동하기 때문에 input 의 대다수는 그대로 지나가고 output 은 그리 크지 않은 변화만 생길 수 있다.

그렇게 되면 local minima 에 빠질 수 있다. (saddle points) 그래서 input 을 복사하여 결과물에 더해주면 output 의 작은 변화로도 결과적으로 큰 차이처럼 보이게 할 수 있다.

Skip connection 은 ResNet 이미지 분류기에서 좋은 성능을 보여서 많이 사용되기 시작했다고 한다. 그래서 Neural network 분야에서는 보편적으로 사용된다고 한다.

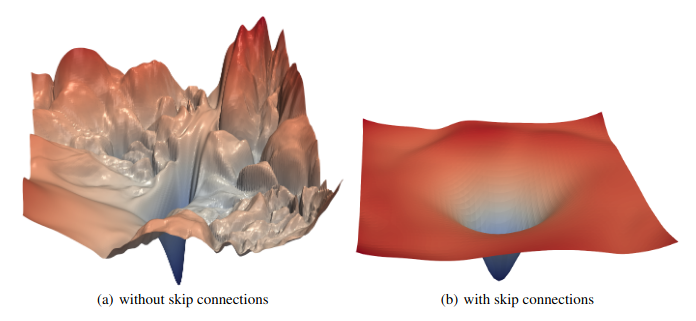
Skip Connection

• Visualizing the Loss Landscape of Neural Nets
• Intuitive Explanation of Skip Connections in Deep Learning

두 번째 목적은 원래 input sequence 를 유지하고자 함이다. 여러 attention head 를 사용함에도 불구하고 학습 과정에서 가장 최근의 단어를 잊어버릴 수 있다.

원래의 어휘를 가지고 있으므로써 여러 복잡한 맥락에서도 강건하게 작동할 수 있다.

Layer normalization

정규화는 skip connection 과 잘 작용하는 방법이다. 대부분 attention 이나 feed forward 과정의 연산 이후에 사용된다.

Transformer 와 같이 움직이는 부분이 많고(여러 layer 들이 있고) 그 중 일부가 matrix multiplication 이 아닌 softmax 나 ReLU 인 구조에서는 값이 얼마나 크고 양수와 음수 사이의 균형을 어떻게 맞추는지가 중요하다.

신경망은 본질적으로 비선형적이기 때문에 signal 의 크기와 분포에도 민감하다. 정규화는 다층 신경망의 각 단계에서 signal 의 일관된 분포를 유지하는 데 유용한 것으로 입증된 기법이다.

Multiple layers

Attention 블록과 신중하게 선택한 가중치가 있는 feed forward 블록만으로도 괜찮은 언어 모델을 만들 수 있음을 살펴보았다. 실제 데이터로 학습할 때는 예시처럼 0과 1로 이루어진 가중치로 학습할 수 없습니다.

처음에는 가중치가 모두 무작위로 선택되고, 대부분은 0에 가깝고, 그렇지 않은 몇 개의 가중치마저 그다지 필요한 가중치가 아닐 것이다.

그 이유는 역전파를 통한 SGD(Stochastic Gradient Descent) 은 꽤 놀라운 일을 할 수 있지만, 운에 많이 의존한다. 정답에 도달하는 방법이 하나만 있어 모델이 잘 작동하는 데 필요한 가중치 조합이 하나만 있다면 그 정답에 제대로 도달하기 매우 어렵다. 하지만 좋은 정답에 이르는 방법이 많다면 모델이 그 답을 찾을 가능성이 훨씬 더 높다.

Attention 계층이 하나만 있으면(Multi-head attention 블록과 feed forward 블록이 하나씩만 있으면) 좋은 parameter 집합에 대한 경로가 하나만 허용된다. 이는 취약하고, 매개변수에 대한 초기 추측이 이상적인 솔루션과는 거리가 먼 솔루션에 갇힐 가능성이 높다.

Transformer 는 여러 개의 attention 계층을 두고 각 계층이 이전 계층의 출력을 입력으로 사용하여 이러한 문제를 해결한다.

Skip connection 을 사용하면 각각의 attention 블록이 실패하거나 불안정한 결과를 낳더라도 전체 파이프라인을 견고하게 만들 수 있다. 본 논문에서는 레이어가 많을수록 성능이 향상되는 것으로 나타났지만, 6개 이후에는 개선이 미미해졌다.

이렇게 여러 레이어를 사용하는 것을 컨베이어 벨트로 생각해볼 수도 있다. 각 attention 블록과 feed forward 블록은 벨트 라인에서 입력을 가져와 유용한 attention 행렬을 계산하고 다음 단어 예측을 할 수 있다. 유용한 결과든 그렇지 않든 컨베이어에 다시 추가되어 다음 레이어로 전달된다.

Decoder stack

Transformer 는 encoder 와 decoder 로 이루어져 있는데 앞서 다룬 구조도는 대부분 decoder 위주로 살펴보았다.

sequence 를 완성하는 작업에서는 decoder 가 부분적인 sequence 들을 완성하고 이를 확장할 수 있다. OpenAI 에서 만든 GPT 의 경우도 encoder 를 제거하고 12 개의 decoder stack 만 사용하였다고 한다.

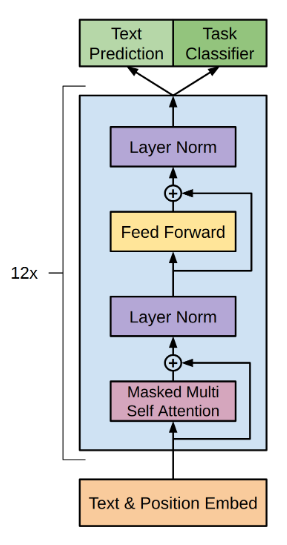
Encoder stack

구조도에서 왼쪽에 위치하는 encoder 는 decoder 와 거의 유사하게 작동한다. 가장 큰 차이는 성능이 어떤지 판단하는 softmax 과정이 최종적으로 이루어지지 않고 여전히 embedded 공간에 있는 vector sequence 라는 점이다.

그래서 굉장히 추상적이기는 하지만 decoder stack 에 들어감으로써, 어떠한 의미를 전달하는데 사용될 것이라는 것을 알 수 있다.

예를 들어 sequence 를 생성하는 것 말고도 다른 언어로 번역하는 과정에서 유용하다. 번역에서는 원본 언어의 sequence 와 대상 언어의 일치하는 sequence 가 모두 필요하기 때문에, encoder 에서는 원본 언어 전체가 실행되고 이 출력이 decoder 계층으로 들어가는 방식으로 작동한다.

Cross-attention

이제 transformer 구조에서 남은 부분은 encoder 와 decoder stack 간의 연결 부분이다.

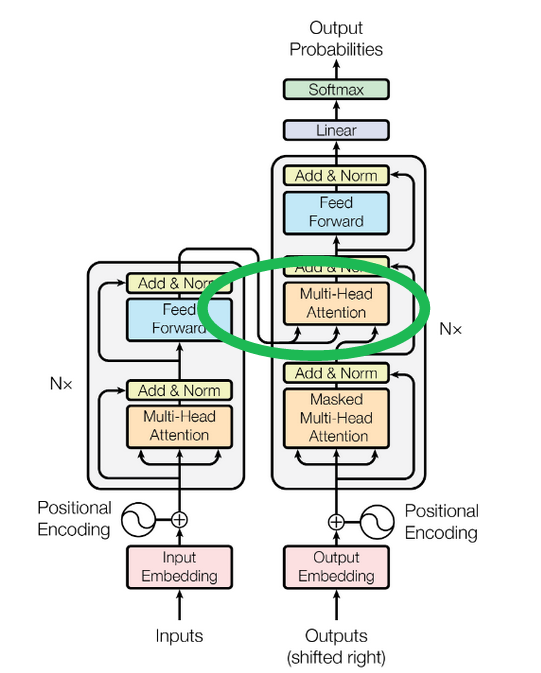
Cross-attention 은 key 행렬 $K$ 와 value 행렬 $V$ 가 이전 decoder stack 의 출력이 아닌 최종 encoder stack 의 출력을 기반으로 한다는 점을 제외하면 기존 attention 과 동일하게 작동한다.

Query 행렬 $Q$ 는 여전히 이전 decoder stack 의 결과에서 계산된다. 따라서 source sequence (Inputs) 의 정보가 target sequence (Outputs) 로 전달되어 올바른 방향으로 결과가 생성되도록 유도하는 채널이라고 이해할 수 있다.

Tokenizing

Transformer 구조에 대해 모두 살펴보았지만 수많은 단어들을 어떤 식으로 데이터화해야하는 지는 자세히 살펴보지 않았다. 사실 실제로 적용하는데 있어서는 중요한 부분일 수 있다.

앞서서 어휘를 표현할 때는 고차원의 one-hot vector 로 표현하여 각 요소들이 각 단어를 나타낸다고 이해하였다. 이렇게 하기 위해서는 얼마나 많은 단어들이 표현되어야 하는지 알아야 한다.

가장 naive 한 방식은 모든 단어들을 나열하는 것일 것이다. 하지만 대부분의 단어들이 복수형이나 소유격, 활용형 등등 여러 형태를 가지고 있다. 또한, 신조어나 속어, 전문용어 혹은 Unicode 로 표현되는 것들도 있다.

다른 방법은 단어가 아니라 개별 문자를 구성 요소로 사용하는 것이다. 전체 문자 목록은 정해져 있기 때문이다.

문제는 우리가 embedding 공간으로 변환할 때 각 거리들이 의미론적 해석이 있다고 가정하였다. 가까운 점끼리 비슷한 의미를 가지도록 하였는데 개별 문자들에서는 (언어따라 다르지만) 이러한 의미론인 내용을 담고 있지 않다.

또한, transformer 에서는 내부적으로 입력 쌍의 집합으로 작동하기 때문에 개별 문자를 사용하게 되면 순서가 무의미한 문자 쌍의 집합이 되어 transformer 를 학습시키는 것이 매우 어려워질 것이다.

실제로, 문자 수준 표현을 사용한 실험에서 transformer 가 그다지 좋은 성능을 내지 못했다고 한다.

Byte pair encoding

다행히 이를 해결하기 위해 좋은 방법인 byte pair encoding 이 있다.

이 방법은 각 문자에 고유한 byte 를 할당하고, 가장 일반적인 byte 쌍을 모아서 새로운 byte 를 할당한다. 이를 다시 새로운 데이터에 대입하여 byte 를 할당하는 과정을 반복한다.

이 방법을 통해 긴 문자의 연속을 나타내는 고유 코드를 얻을 수 있고, 길이의 제한이 없게 된다. 그리고 모든 문자조합을 표현하는 대신 데이터에서 학습하기 때문에 필요한 문자들만 얻게 된다. 예를 들어 transformer 와 같은 긴 단어는 표현하지만 dklfjqlqdja 와 같이 의미없는 무의미한 문자열에는 byte 를 할당하지 않는다.

그리고 단순한 문자 조합이나 단어 나열로 해결하기 힘든 신조어, 외국어 등도 표현이 가능해진다.

Byte pair encoding 을 사용하면 어휘의 크기를 지정해서 해당 크기에 도달할 때까지 새 고유코드를 생성할 수 있다. 그래서 문자열들이 텍스트의 의미적 내용을 포함할 수 있을 정도로 길어지면, transformer 에 사용할 수 있게 된다.

어떤 문장이나 단락을 transformer 에 넣을 때 byte pair encoder 로 전처리하면 인식 가능한 단어들 끼리 고유한 chunk 로 나누어 각각 고유 코드를 부여하게 될 것이다. 그래서 이 과정을 tokenization 이라고 한다.

---

마무리

LLM 을 공부하기 전에 Transformer 부터 이해해보자 하고 여러 글들을 찾다가 아주 기초부터 단단하게 다루는 post 가 있어 읽어보았다.

영어로 너무 길고 생소한 표현들이 많아 여러 번 읽었고, 정리하면서 한글 번역하면서도 너무 오래 걸렸다.

하지만 정리하면서 영어로 읽을 때 대강 읽어 지나쳤던 부분들이 확실해지면서 혼자 대략 설명할 수 있게 이해하였다.

Karpathy 의 Let’s build GPT 와 Annotate Transformer 를 해보면서 코드로 구현도 해보고 싶은데, 과연 이 과정이 LLM 을 로보틱스에 적용하는데도 필요한 걸까 하는 불안함을 가지고 있다.

아마도 벽을 짚으면서 공부하는 느낌이라 (누가 먼저 해놓은 것이 많이 없다보니) 그렇지 않을까 싶은데 3월 전에는 어떤 방향성을 찾지 않을까…!

다음에 할 것

The Annotated Transformer