[CDC '10] Geometric Tracking Control of a Quadrotor UAV on SE(3)

Geometric Tracking Control of a Quadrotor UAV on $\mathbf{SE}(3)$

드론 제어에서 많이 인용되는 이태영 교수님의 “Geometric Tracking Control of a Quadrotor UAV on SE(3)” 논문을 읽어보았다.

논문 제목 그대로 $\mathbf{SE}(3)$ 에서 desired state 를 추종하는 controller 를 제안하였다.

앞선 Whole-body Motion Planning 논문들에서 여러 차례 attitude 를 고려하기 위해 $\mathbf{SE}(3)$ 에서의 경로 생성이 필요하다고 언급하였는데, Lie theory 까지 파고들기 어려워 To-Do 로 남겨두었는데, 본 논문을 보면서 이해가능한 정도로만 살펴보기로 하였다.

Contributions

• almost global 한 control system 을 제안하여 어떤 initial state 에서도 desired state 로 제어가 가능하다.

Introduction

기존 UAV 의 제어와 관련한 연구에서는 nonlinear control 보다는 linear control system 을 많이 사용했다고 한다.

선행 연구들 조차도 quadrotor dynamics 를 선형화하거나 backstepping 과 sliding mode 방식이 사용되었고 이들은 모두 오일러 각에서 이루어졌기 때문에 singularity 문제에서 벗어날 수 없었다.

nonlinear manifolds 에서 전개된 dynamics 를 위한 Geometric Control 은 Euclidean 공간에서 표현할 수 없는 공간에서 제어가 가능하다.

따라서 본 논문에서는 $\mathbf{SE}(3)$ 에서 quadrotor dynamics 를 전개하고 이를 통해 경로 추종 제어기를 제안하였다.

Quadrotor Dynamics Model

Coordinate Frame

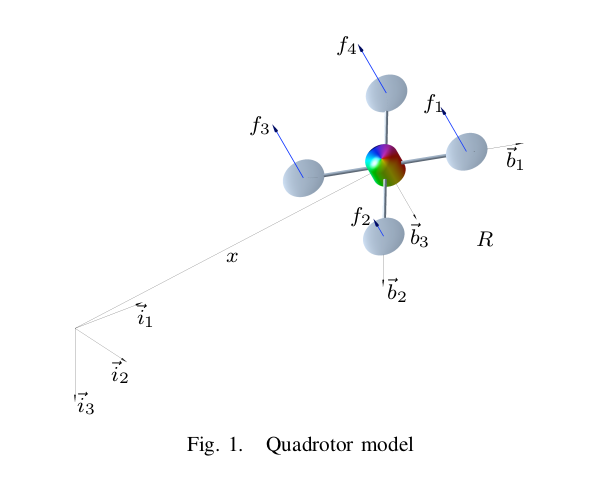
그림과 같이 inertial frame $\{{\vec{i}}_1,{\vec{i}}_2,{\vec{i}}_3\}$ 과 body-fixed frame $\{{\vec{b}}_1,{\vec{b}}_2,{\vec{b}}_3\}$ 을 정의한다. 이 외에 $m,J,R,\Omega$ 는 관습적인 정의를 따른다. ($\Omega$ 는 각속도)

quadrotor 는 4개의 모터의 thrust input 으로 6 DoF 움직임을 만들어 내는 underactuated system 이다.

${\mathbb{R}}^3$ 에서 translation, $\mathbf{SO}(3)$ 에서 rotation 을 표현하므로 이는 $\mathbf{SE}(3)$ 의 configuration manifold 를 가진다.

What is configuration manifold?

• The space of all posible coordinates needed to determine the system (ref)
• 즉, system 을 온전히 표현하기 위해 필요한 좌표공간

$\mathbf{SO}(3)$ 란 special orthogonal group 의 약자로 $\{R\in {\mathbb{R}}^{3\times 3}|R^{T}R=1,\det R=1\}$ 로 표현된다. 즉, 3차원 회전행렬 $R$ 의 연산들로 닫혀있는 군이다.

What is Group?

군 (Group) 은 간단하게 집합 $G$ 와 어떤 연산자(binary operator, 이항연산자) $\ast$ 로 이루어진 구조에 대한 개념이다.

$G$ 의 요소와 연산자 $\ast$ 에 대해 아래와 같은 조건을 만족해야 한다.

• Composition: 모든 $a,b\in G$ 는 연산자 $\ast$ 에 대해 닫혀있다. 즉, $a\ast b\in G$ 를 만족한다.
• Associativity: 모든 $a,b,c\in G$ 에 대해 $(a\ast b)\ast c=a\ast (b\ast c)$ 를 만족한다.
• Identity element: 항등원이 존재한다. 즉 모든 $a\in G$ 에 대해 $a\ast e=e=e\ast a$ 를 만족하는 $e\in G$ 가 존재한다.
• Inverse element: 역원이 존재한다. 모든 $a\in G$ 에 대해 항등원 $e$ 와 $a\ast b=e=b\ast a$ 를 만족하는 unique 한 $b\in G$ 가 존재한다.

자세한 내용은 Wikipedia 를 참고하자.

special Euclidean group $\mathbf{SE}(3)$ 는 따라서 아래와 같이 정의된다.

$$\mathbf{SE}(3)=\{T=\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]\in {\mathbb{R}}^{4\times 4}|R\in \mathbf{SO}(3),t\in {\mathbb{R}}^3\}$$

Dynamic Model

그림에 표현된 대로 전체 thrust 는 $-{\vec{b}}_3$ 방향을 가지는 $f={\sum }_{i=1}^4{f}_i$ 로 표현된다. 이를 inertial frame 으로 표현하면 $-fR{e}_r\in {\mathbf{R}}^3$ 가 된다.

${\vec{b}}_i$ 는 ${\mathbb{R}}^3$ 에서 각 축의 unit vector $e_i$ 에 대해 $R{e}_i$ 로 표현된다.

이제 $f_i$ 를 가지고 $R$ 을 얻어내기 위해서는 torque 를 고려해야 한다. 대부분 그렇듯 각 모터와 프롭의 dynamics 까지 고려하기는 어려우므로 torque 와 thrust 가 비례한다고 가정한다.

그리고 첫 번째와 세 번째 프롭이 CW 방향으로 돌고, 나머지가 CCW 로 돈다고 두면 아래와 같이 전체 thrust $f$ 와 moment $M$ 을 표현할 수 있다.

$$\left[\begin{array}{c}f\\ M_1\\ M_2\\ M_3\end{array}\right]=\left[\begin{array}{cccc}1& 1& 1& 1\\ 0& -d& 0& -d\\ d& 0& -d& 0\\ -c_{\tau f}& -c_{\tau f}& -c_{\tau f}& -c_{\tau f}\end{array}\right]\left[\begin{array}{c}{f}_1\\ f_2\\ f_3\\ f_4\end{array}\right]\text{\hspace{1em}(1)}$$

이 때 torque ${\tau }_i=(-1{)}^i{c}_{\tau f}{f}_i$ 로 표현된다. 위의 $4\times 4$ 행렬이 invertible 하므로 $f\in \mathbb{R}$ 와 $M\in {\mathbb{R}}^3$ 을 control input 으로 사용할 수 있다.

따라서 quadrotor 의 equations of motion 을 아래와 같이 정리할 수 있다.

$$\begin{array}{rl}\dot{x}& =v\\ m\dot{v}=m& g{e}_3-fR{e}_3\\ \dot{R}& =R\hat{\Omega }\\ J\dot{\Omega }+\Omega & \times J\Omega =M\end{array}\text{\hspace{1em}(2)(3)(4)(5)}$$

여기서 hat map $\hat{\cdot }:{\mathbb{R}}^3\to \mathfrak{so}(3)$ 은 $\hat{x}y=x\times y\forall x,y\in {\mathbb{R}}^3$ 를 만족하는 연산자이다.

즉, ${\mathbb{R}}^3$ 에 있는 vector 를 skew-symmetric matrix 바꿔준다. $\vec{\Omega }=[{\Omega }_x,{\Omega }_y,{\Omega }_z{]}^T\in {\mathbb{R}}^3$ 에 대해 hat map 이 아래와 같이 표현된다.

$$\hat{\vec{\Omega }}=\left[\begin{array}{ccc}0& -{\Omega }_z& {\Omega }_y\\ {\Omega }_z& 0& -{\Omega }_x\\ -{\Omega }_y& {\Omega }_x& 0\end{array}\right]$$

아래 영상이 큰 도움이 되었다.

Geometric Tracking Control on SE(3)

주어진 경로는 CoM 의 위치와 ${\vec{b}}_1$ 의 방향으로 이루어져 있다. 이를 각각 $x_d(t),{\vec{b}}_{1_d}(t)$ 라고 한다.

translation dynamics 는 $-fR{e}_3$ 에 의해 제어되므로 $x_d(t)$ 로 이동하기 위해 적절한 $f$ 와 ${\vec{b}}_{3_d}(t)$ 를 선택해야 한다.

그리고 ${\vec{b}}_{3_d}(t)$ 가 정해지면 desired attitude $R_d\in \mathbf{SO}(3)$ 를 결정하기 위해 하나의 요소가 더 필요하다. 즉 ${\vec{b}}_3$ 에 수직인 평면에 있는 quadrotor 의 방향이 정해져야 한다.

이는 앞서 ${\vec{b}}_{1_d}(t)$ 에 의해 정해진다.

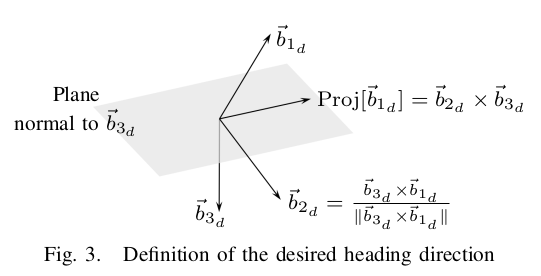
${\vec{b}}_{1_d}(t)$ 는 ${\vec{b}}_{3_d}(t)$ 에 평행하지 않다고 가정하므로, 이를 ${\vec{b}}_{3_d}(t)$ 을 법선으로 삼는 평면에 투영(projection) 한다. 이로써 desired attitude $R_d=[{\vec{b}}_{2_d}\times {\vec{b}}_{3_d},{\vec{b}}_{2_d},{\vec{b}}_{3_d}]\in \mathbf{SO}(3)$ 가 결정된다.

이 때 ${\vec{b}}_{2_d}=\frac{{\vec{b}}_{3_d}\times {\vec{b}}_{1_d}}{\Vert {\vec{b}}_{3_d}\times {\vec{b}}_{1_d}\Vert }$ 이다. 이 $R_d$ 를 따라가기 위해 $M$ 이 결정된다.

요약하자면, $t\to \infty$ 에 따라 $x(t)\to x_d(t)$ 와 $\text{Proj}[{\vec{b}}_1(t)]\to \text{Proj}[{\vec{b}}_{1_d}(t)]$ 을 만족한다.

$\text{Proj}$ 는 앞서 설명한 대로 ${\vec{b}}_{3_d}$ 에 수직한 평면으로 정규화한 투영을 의미한다. 자세한 내용은 그림 3 참고.

보다시피, Lie group 에서 바로 사용할 수 있는 제어기이므로 singularity 로부터 자유롭고 좌표계 변환이 필요없다.

A. Tracking Errors

이제 $x,v,R,\Omega$ 에 대해 tracking error 를 정의해야 한다. 위치와 속도에 대해서는 아래와 같이 간단하게 정의할 수 있다.

$$\begin{array}{r}{e}_x=x-x_d\\ e_v=v-v_d\end{array}\text{\hspace{1em}(6)(7)}$$

attitude $R$ 과 각속도 $\Omega$ 는 $\mathbf{TSO}(3)$ (the tangent bundle of $\mathbf{SO}(3)$) 에서 전개되므로 복잡한 수식 전개가 필요하다.

우선 $\mathbf{SO}(3)$ 에서 error function 을 아래와 같이 정의한다.

$$\Psi (R,R_d)=\frac{1}{2}\text{tr}[I-R_d^{T}R]\text{\hspace{1em}(8)}$$

$R$ 과 $R_d$ 의 각도 차이가 $180^{\circ }$ 이내인 영역에서 $R=R_d$ 라면 locally positive-defnite 하다.

그리고 이에 대한 sublevel set $L_2$ 을 정의한다.

$$L_2=\{R_d,R\in \mathbf{SO}(3)|\Psi (R,R_d)<2\}$$

풀어보면 둘의 각도 차이가 $180^{\circ }$ 라면 $R_d^{T}R=\left[\begin{array}{ccc}-1& 0& 0\\ 0& -1& 0\\ 0& 0& 1\end{array}\right]$ 이다. 따라서 이 때의 $\Psi (R,R_d)$ 값은 2가 된다.

그러므로 $L_2$ 는 $180^{\circ }$ 이내의 각의 집합이므로 논문 표현대로 almost covers $\mathbf{SO}(3)$ 한다.

회전 행렬 $R$ 의 변화를 $\delta R=R\hat{\eta }\text{for}\eta \in {\mathbb{R}}^3$ 로 표현하면 위의 error function $\Psi$ 의 미분은 아래와 같다.

$${\mathbf{D}}_R\Psi (R,R_d)\cdot R\hat{\eta }=-\frac{1}{2}\text{tr}[R_d^{T}R\hat{\eta }]=\frac{1}{2}(R_d^{T}R-R^T{R}_d{)}^{\vee }\cdot \eta \text{\hspace{1em}(9)}$$

이 때 vee map $\vee :\mathfrak{so}(3)\to {\mathbb{R}}^3$ 은 위에서 hat map $\widehat{(}\cdot )$ 의 역함수이다.

Question

• Equation (9) 의 유도과정

이로부터 attitude tracking error $e_R$ 을 아래와 같이 정의한다.

$$e_R=\frac{1}{2}(R_d^{T}R-R^T{R}_d{)}^{\vee }\cdot \text{\hspace{1em}(10)}$$

두 접벡터( tangent vector ) $\dot{R}\in {\mathbf{T}}_{\mathbf{R}}\mathbf{SO}(3)$ 와 ${\dot{R}}_d\in {\mathbf{T}}_{{\mathbf{R}}_{\mathbf{d}}}\mathbf{SO}(3)$ 는 서로 다른 tangent space 에 놓여있으므로 바로 비교할 수 없다.

그래서 ${\dot{R}}_d$ 를 ${\mathbf{T}}_{\mathbf{R}}\mathbf{SO}(3)$ 공간의 벡터로 변환한 후에 $\dot{R}$ 과 비교한다.

$$\dot{R}-{\dot{R}}_d(R_d^{T}R)=R\hat{\Omega }-R_d\widehat{{\Omega }_d}{R}_d^{T}R=R(\Omega -R^T{R}_d{\Omega }_d{)}^{\wedge }$$

Question

• 위 수식 뒷 부분 수식 전개

이로써, 각속도에 대한 추종 오차를 다음과 같이 정의한다.

$$e_{\Omega }=\Omega -R^T{R}_d{\Omega }_d\text{\hspace{1em}(11)}$$

$\frac{d}{dt}(R_d^{T}R)=(R_d^{T}R){\hat{e}}_{\Omega }$ 이므로 $e_{\Omega }$ 가 회전행렬 $R_d^{T}R$ 의 각속도 임을 알 수 있다.

B. Tracking Controller

경로로부터 주어진 $x_d(t),{\vec{b}}_{1_d}(t)$ 와 양의 상수 $k_x,k_v,k_R,k_{\Omega }$ 로부터 아래와 같이 ${\vec{b}}_{3_d}$ 를 정의한다.

$${\vec{b}}_{3_d}=\frac{-k_x{e}_x-k_v{e}_v-mg{e}_3+m{\ddot{x}}_d}{\Vert -k_x{e}_x-k_v{e}_v-mg{e}_3+m{\ddot{x}}_d\Vert }\text{\hspace{1em}(12)}$$

당연히 분모 $\Vert -k_x{e}_x-k_v{e}_v-mg{e}_3+m{\ddot{x}}_d\Vert \ne 0$ 임을 가정한다.

앞서 정의한 $R_d$ 에 대해 control inputs $f,M$ 은 아래와 같이 구성한다.

$$\begin{array}{rl}f& =-(-k_x{e}_x-k_v{e}_v-mg{e}_3+m{\ddot{x}}_d)\cdot R{e}_3\\ M& =-k_R{e}_R-k_{\Omega }{e}_{\Omega }+\Omega \times J\Omega -J(\hat{\Omega }{R}^T{R}_d{R}_{\Omega }-R^T{R}_d{\dot{\Omega }}_d)\end{array}\text{\hspace{1em}(15)(16)}$$

Question

• 수식 (16) 에서 $\hat{\Omega }{R}^T{R}_d{R}_{\Omega }-R^T{R}_d{\dot{\Omega }}_d$ 부분이 어떻게 생기게 된 것인지?
• 수식(3) 이 inertial frame 에서 정의된 것으로 이해했는데 그렇다면 (15) 는 body-fixed frame 에서의 $f$ 를 의미하는 것인가? $R{e}_3$ 부분이 곱해진 이유?

Solved

• 수식(3) 에 $R{e}_e$ 가 곱해진 이유는 아래 설명되어 있듯이, attitude error 에 따라 전체 thrust 의 크기를 작게 하기 위함이다.

이 때 desired trajectory 에서 필요한 net force 는 다음과 같이 주어진 상수 $B$ 보다 작다.

$$\Vert -mg{e}_3+m{\ddot{x}}_d\Vert <B\text{\hspace{1em}(14)}$$

(16) 에서의 control moment $M$ 은 $\mathbf{SO}(3)$ 에 상응하는 추종 제어기이다. 수식 (4), (5) 에서 제시된 dynamics 대로 이 제어기는 attitude tracking error 를 기하급수적으로 줄인다.

마찬가지로 (15) 에서의 제어기는 ${\mathbb{R}}^3$ 에서의 translational dynamics 를 반영한다. attitude tracking error 가 없음을 전제로 $-fR{e}_3$ 가 translation 에 대한 추종 제어를 할 수 있다.

따라서, attitude tracking error 가 0이 되면서 translational tracking error 가 0으로 수렴하게 된다.

물론 순간적으로 attitude tracking error 가 0이 아닐 수 있고, attitude error 가 커지면 $fR{e}_3$ 의 방향이 desired direction $R_d{e}_3$ 의 방향으로부터 많이 벗어날 수 있다.

그래서 (15) 에서 attitude tracking error 가 크면 전체 thrust $f$ 의 크기가 작아지도록 하였다.

$f$ 의 수식에 desired body-fixed axis ${\vec{b}}_{3_d}=R_d{e}_3$ 오 현재의 body-fixed axis ${\vec{b}}_3=R{e}_r$ 의 dot product $\cdot$ 을 포함하였다.

C. Exponential Asymptotic Stability

D. Almost Global Exponential Attractiveness

E. Properties and Extensions

Conclusion

본 논문은 $\mathbf{SE}(3)$ 에서의 geometric controller 를 제안하여 오일러각이나 쿼터니언에서의 단점을 극복할 수 있었다.

또한, 처음 attitude error 가 $90^{\circ }$ 라면 기하급수적으로 안정화되고 $180^{\circ }$ 이내라면 다시 $90^{\circ }$ 이내의 오차로 수렴하면서 almost global 함을 보였다.