[CS285] 4. Introduction to Reinforcement Learning

Lecture 4: Introduction to Reinforcement Learning

https://rail.eecs.berkeley.edu/deeprlcourse/deeprlcourse/static/slides/lec-4.pdf

Part 1

Reward functions

$r(s,a)$ 로 표현하는 보상함수는 어떤 state 와 action 이 좋은지 판별해주는 기준이다. 강화학습에서 앞으로의 timestep 에서 얻을 수 있는 미래의 보상을 크게 얻고자 한다.

Markov chain

$$\mathcal{M}=\{\mathcal{S},\mathcal{T}\}$$

$\mathcal{S}$ - state space, state $s\in \mathcal{S}$

$\mathcal{T}$ - transition operator $p(s_{t+1}|s_t)$

“operator” (연산자) 로 부르는 이유는 각 상태에서의 전환될 확률 $p(s_t=i)$ 을 벡터 ${\mu }_{t,.i}$ 로 나타내면 transition probability 를 행렬 ${\mathcal{T}}_{i,j}=p(s_{t+1}=i|s_t=j)$ 로 표현할 수 있고, 이를 행렬 곱으로 다음 상태 확률 벡터 ${\mu }_{t+1}$ 를 구할 수 있기 때문이다.

$${\vec{\mu }}_{t+1}=\mathcal{T}{\vec{\mu }}_t$$

Markov decision process

$$\mathcal{M}=\{\mathcal{S},\mathcal{A},\mathcal{T},r\}$$

$\mathcal{S}$ - state space, state $s\in \mathcal{S}$

$\mathcal{A}$ - action space, action $a\in \mathcal{A}$

$\mathcal{T}$ - transition operator (now a tensor! = 3D matrix)

이전과 마찬가지로 상태에서 전이할 확률 ${\mu }_{t,j}=p(s_t=j)$ 와 새로 더해진 행동이 선택될 확률 ${\xi }_{t,k}=p(a_t=k)$ 라고 하면 전이 행렬 ${\mathcal{T}}_{i,j,k}=p(s_{t+1}=i|s_t=j,a_t=k)$ 로 표현할 수 있다. 즉, $s_t$ 에서 선택한 $a_t$ 로 $s_{t+1}$ 이 될 확률이다.

이를 선형방정식으로 표현하면 ${\mu }_{t+1,i}={\sum }_{j,k}{\mathcal{T}}_{i,j,k}{\mu }_{t,j}{\xi }_{t,k}$ 이 된다.

$r$ - reward function $r:\mathcal{S}\times \mathcal{A}\to \mathbb{R}$

Partially observed Markov decision process (POMDP)

$$\mathcal{M}=\{\mathcal{S},\mathcal{A},\mathcal{O},\mathcal{T},\mathcal{E},r\}$$

이제 Markov decision process 에 observation space $\mathcal{O}$ 와 emission probability $\mathcal{E}=p(o_t|s_t)$ 가 더해져 부분적으로 관측한 Markov decision process 가 구성된다.

The goal of reinforcement learning

NN 으로 구성한 policy ${\pi }_{\theta }(a|s)$ 는 상태를 행동으로 맵핑한다. $\pi :s\to a$ 이를 통해 이동한 다음 state 는 다시 policy 를 거쳐 action 을 선택한다.

이를 horizon $T$ 에 대해 $s_T$ 에 도달할 때 까지의 궤적으로 표현할 수 있다.

$$p_{\theta }(\tau )=p_{\theta }(s_1,a_1,\dots ,s_T,a_T)=p(s_1)\prod _{t=1}^T{\pi }_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t)$$

Markov cahin 과 chain rule 을 통해 간략히 표현할 수 있다.

그리고 궤적 분포를 바탕으로 기댓값을 정의할 수 있다. 그러므로 기댓값을 최대화하는 매개변수 $\theta$ 를 찾는 것으로 강화학습의 목표함수를 정의할 수 있다.

$${\theta }^{\ast }=\arg \underset{\theta }{\max }{E}_{\tau \sim p_{\theta }(\tau )}[\sum _{t}r(s_t,a_t)]$$

위의 궤적 분포 $p_{\theta }(\tau )$ 의 상태들이 이동하는 부분을 markov chain 으로 재정의할 수 있다. 즉, 주어진 $s_t,a_t$ 에 대해 $s_{t+1},a_{t+1}$ 로 이동할 확률 $p((s_{t+1},a_{t+1})|(s_t,a_t))$ 로 표현된다.

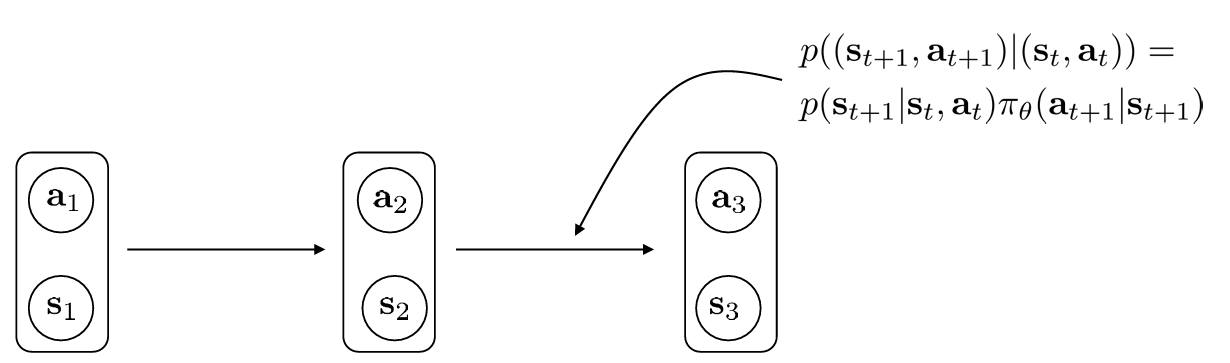
Finite horizon case: state-action marginal

이를 이용해 목적함수도 재정의할 수 있다.

$$\begin{array}{rl}{\theta }^{\ast }& =\arg \underset{\theta }{\max }{E}_{\tau \sim p_{\theta }(\tau )}[\sum _{t}r(s_t,a_t)]\\ & =\arg \underset{\theta }{\max }\sum _{t=1}^T{E}_{(s_t,a_t)\sim p_{\theta }(s_t,a_t)}[r(s_t,a_t)]\end{array}$$

Infinite horizon case: stationary distribution

여기에서 정해진 horizon 이 아니라 무한하게 된다면 어떻게 되는지 알아보자.

$p(s_t|a_t)$ 이 고정분포로 수렴하게 된다면 결국 $\mu =\mathcal{T}\mu$ 로 표현가능하게 된다.

따라서 무한한 시간이 지나게되면 $\mu =p_{\theta }(s,a)$ 인 고정분포가 된다.

목적함수의 경우에는 $T$ 가 무한할 떄 보상함수의 기댓값도 무한해지므로 discount factor $\gamma$ 를 사용하거나 $T$ 로 나눠 평균값을 얻는 방식이 있다.

$${\theta }^{\ast }=\arg \underset{\theta }{\max }\frac{1}{T}\sum _{t=1}^T{E}_{(s_t,a_t)\sim p_{\theta }(s_t,a_t)}[r(s_t,a_t)]$$

위에서 얘기한대로 무한한 시간이 흐르면 결국 모든 항이 고정분포에 근접한 항들이므로 $T$ 만큼의 시간에서 얻은 보상의 평균은 아래와 같이 생략된다.

$${\theta }^{\ast }=\arg \underset{\theta }{\max }{E}_{(s,a)\sim p_{\theta }(s,a)}[r(s,a)]$$

Expectations and stochastic systems

보상이 scalar 이라 불연속적이고 미분불가능함에도 불구하고 강화학습에서 경사하강법 같은 최적화 방법을 사용할 수 있는 이유는

$r(\mathbf{x})$ - not smooth 이지만 여기에서 좋은 행동을 선택할 확률이 매개변수 $\theta$ 로 표현되기 때문이다.

즉, ${\pi }_{\theta }(\mathbf{a}=\text{fall})=\theta$ 이기 때문에 이에 대한 보상의 기댓값 $E_{{\pi }_{\theta }}[r(x)]$ 은 $\theta$ 에 대해 smooth 하다.

Part 2. Algorithms

The anatomy of a reinforcement learning algorithm

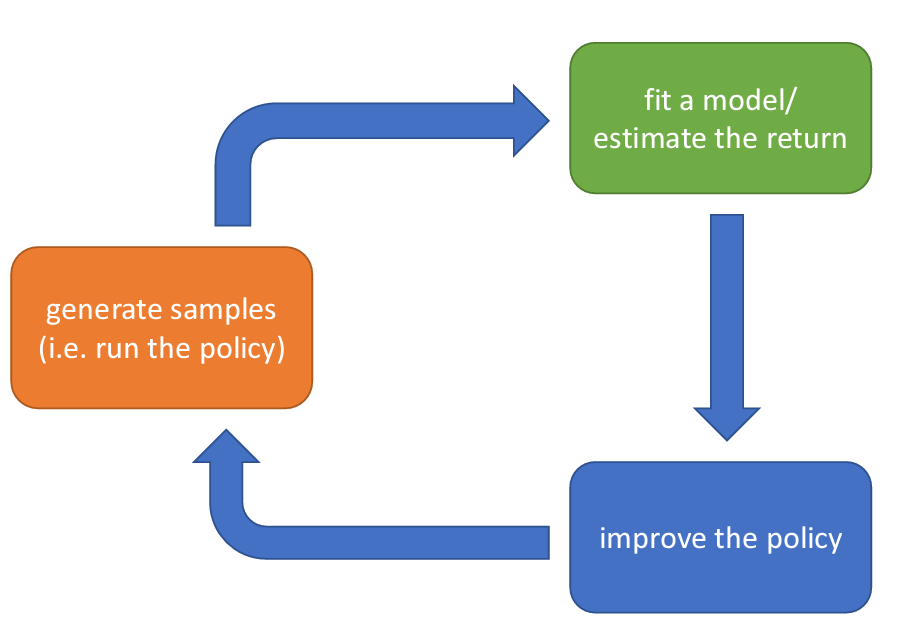
위와 같은 구조도로 RL 알고리즘이 작동한다.

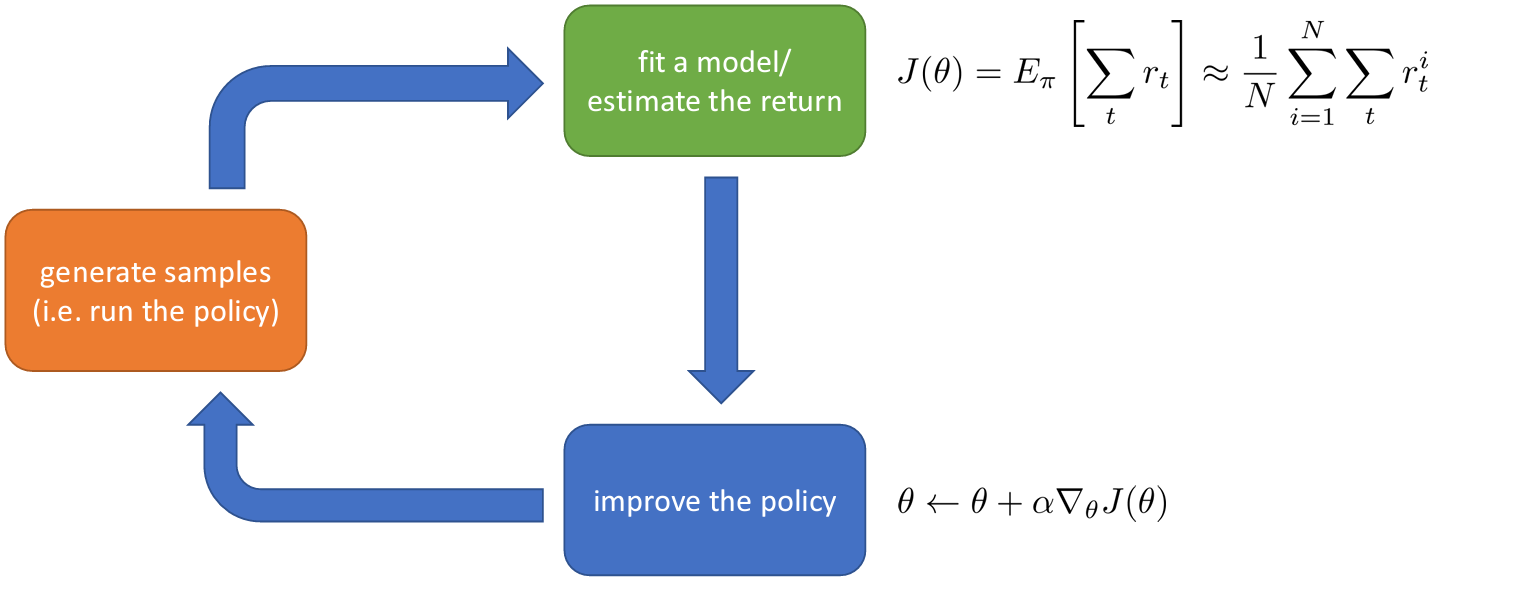
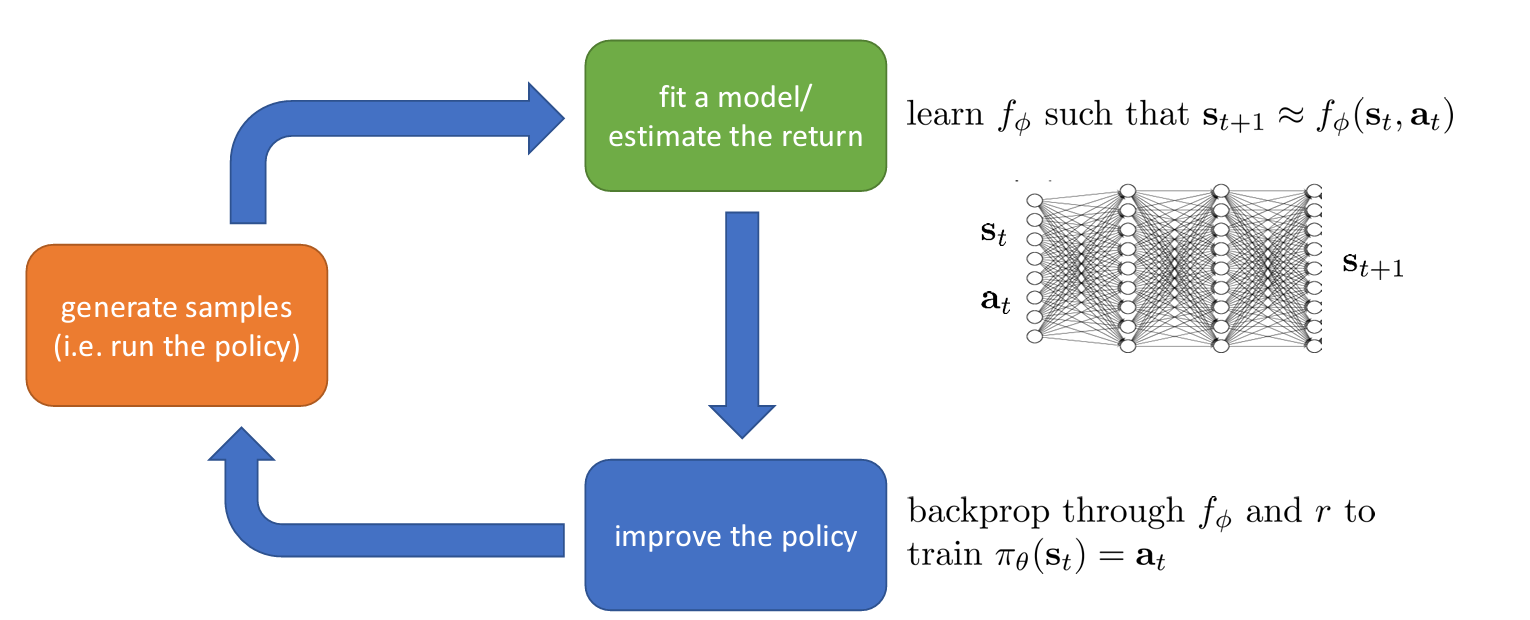
간단한 경우에는 보상을 합산하고 이를 이용해 정책을 개선할 수 있다.

신경망을 학습하는 경우에는 조금 더 복잡할 수 있다. $s_t,a_t$ 에서 $s_{t+1}$ 로 이동하는 전이함수를 학습시키고, 역전파 과정을 통해 ${\pi }_{\theta }(s_t)=a_t$ 를 더 큰 $r$ 을 얻도록 한다.

Whici parts are expensive?

위 과정 중에서 어떤 과정이 가장 비용이 많이 들까?

샘플을 생성하는 경우 실제 환경에서는 직접 샘플을 수집해야 하기 때문에 시간과 비용이 매우 많이 들 수 있다. 하지만 시뮬레이션을 통해 하는 경우 실제 시간의 몇 천~만 배 빠르게 수집할 수 있어 때로는 사소할 수 있다.

보상을 추정하는 경우에는 단순히 합산을 하므로 빠르고, 적은 비용이 들지만 신경망을 학습하는 경우에는 비쌀 수 있다.

마찬가지로 정책을 개선하는 경우도 상황에 따라 다르다. 앞으로 각 알고리즘을 살펴보며 어떤 부분에 집중하는지 혹은 비용이 많이 드는지 알아본다.

Part 3: Value Functions

How do we deal with all these expectations?

$$E_{\tau \sim p_{\theta }(\tau )}[\sum _t^{T}r(s_t,a_t)]$$

우리가 알고있는 기댓값 계산을 풀어적으면 연속적인 기댓값으로 이루어진 수식으로 표현된다.

$$E_{s_1\sim p(s_1)}[E_{a_1\sim \pi (a_1|s_1)}[r(s_1,a_1)+E_{s_2\sim p(s_2|s_1,a_1)}[E_{a_1\sim \pi (a_2|s_2)}[r(s_2,a_2)+\dots |s_2]|s_1,a_1]|s_1]]$$

연쇄되는 부분을 새로운 함수 $Q(s_i,a_i)$ 로 표현하면 아래와 같이 정리된다.

$$E_{\tau \sim p_{\theta }(\tau )}[\sum _t^{T}r(s_t,a_t)]=E_{s_1\sim p(s_1)}[E_{a_1\sim \pi (a_1|s_1)}[Q(s_1,a_1)|s_1]]$$

Definition: Q-function

$$Q^{\pi }(s_t,a_t)=\sum _{t^{\prime }=t}^T{E}_{{\pi }_{\theta }}[r(s_{t^{\prime }},a_{t^{\prime }})|s_t,a_t]$$

이는 $s_t$ 에서 $a_t$ 를 선택함으로써 얻는 전체 보상의 합이다.

Definition: value function

$$\begin{array}{rl}{V}^{\pi }(s_t)& =\sum _{t^{\prime }=t}^T{E}_{{\pi }_{\theta }}[r(s_{t^{\prime }},a_{t^{\prime }})|s_t]\\ & =E_{a_t\sim \pi (a_t|s_t)}[Q^{\pi }(s_t,a_t)]\end{array}$$

가치 함수는 $s_t$ 에서 얻을 수 있는 전체 보상의 합이다. 그리고 이를 (4) 와 같이 $Q^{\pi }$ 를 이용해 표현할 수도 있다.

궁금한 점: (3) 에 있던 $\sum$ 이 없는 이유는 $Q^{\pi }$ 식의 $\sum$ 으로 표현되고, given $a_t$ 가 $E_{a_t\sim \pi (a_t|s_t)}$ 로 바뀌어서인가?

이제 강화학습의 목적함수는 아래와 같이 간단히 표현된다.

$$E_{\tau \sim p_{\theta }(\tau )}[\sum _t^{T}r(s_t,a_t)]=E_{s_1\sim p(s_1)}[E_{a_1\sim \pi (a_1|s_1)}[Q(s_1,a_1)|s_1]]=E_{s_1\sim p(s_1)}[V^{\pi }(s_1)]$$

Using Q-functions and value functions

Part 4: Types of Algorithms

Part 5: Tradeoffs Between Algorithms

Why so many RL algorithms?

• Difference tradeoffs
  • Sample efficiency
  • Stability & ease of use
• Different assumptions
  • Stochastic or deterministic?
  • Continuous or discrete?
  • Episodic or infinite horizon?
• Different things are easy or hard in different settings
  • Easier to represent the policy?
  • Easier to represent the model?

Comparison: sample efficiency

• Sample efficiency = how many samples do we need to get a good policy?
• is the algorithm off policy?
  • Off policy: 새로운 샘플을 만들지 않고 정책을 개선
  • On policy: 정책이 바뀔 때마다 새로운 샘플을 만들어야 함

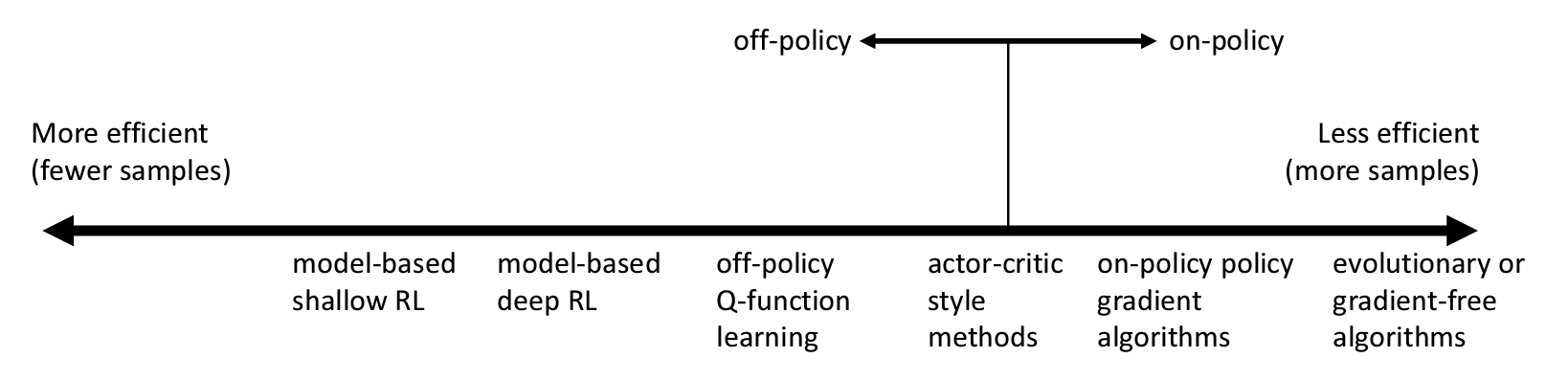효율성이 떨어지는 알고리즘을 쓰는 이유는 다른 장단점이 상황에 따라 유리하지 않을 수 있기 때문이다.

예를 들어 계산 시간이 매우 빨라 새로운 샘플을 만드는 것이 크게 시간이 많이 들지 않는 경우에는 샘플 효율성을 크게 신경쓰지 않아도 된다.

Comparison: stability and ease of use

• Does it converge?
• And if it converges, to what? local minima?
• And does it converge every time?

이러한 질문들이 필요한 이유는 Supervised learning 과 강화학습은 때때로 경사하강과 관련이 없기 때문이다.

Comparison: assumptions

Part 6: Examples of Algorithms

Examples of specific algorithms