[CS285] 5. Policy Gradients

Lecture 5: Policy Gradients

이전 강의에서 다룬 여러 알고리즘 중 Policy gradients 에 대해 먼저 다뤄본다.

Part 1.

The goal of reinforcement learning

강화학습의 목적은 기대되는 보상을 크게 하는 것이었고, $\theta$ 로 변수화된 policy 로 얻어지는 아래와 같이 표현하였다.

$$p_{\theta }(\tau )=p(s_1)\prod _{t=1}^T{\pi }_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t)$$

그리고 horizon $T$ 가 유한하냐 무한하냐에 따라 다르게 표현되지만 아래와 같이 최적의 $\theta$ 인 ${\theta }^{\ast }$ 를 표현하 수 있다.

$$\begin{array}{rl}{\theta }^{\ast }& =\arg \underset{\theta }{\max }{E}_{\tau \sim p_{\theta }(\tau )}[\sum _{t}r(s_t,a_t)]\\ & =\arg \underset{\theta }{\max }{E}_{(s,a)\sim p_{\theta }(s,a)}[r(\mathbf{s},\mathbf{a})]\\ & =\arg \underset{\theta }{\max }\sum _{t=1}^T{E}_{(s_t,a_t)\sim p_{\theta }(s_t,a_t)}[r(s_t,a_t)]\end{array}\text{\hspace{1em}(infinite)(finite)}$$

Evaluating the objective

그러면 목적함수 $J(\theta )$ 를 아래와 같이 표현할 수 있다.

$$J(\theta )=E_{\tau \sim p_{\theta }(\tau )}[\sum _{t}r(s_t,a_t)]\approx \frac{1}{N}\sum _i\sum _{t}r(s_{i,t},a_{i,t})$$

여기서 $i$ 는 $i$ 번 째 샘플을 의미하는 것으로 샘플링된 궤적에 대한 reward 들을 평균냄으로써 목적함수를 근사하여 얻어낸다.

Direct policy differentiation

단순히 평균내는 것에서 이를 더 개선하고 싶기 때문에 목적함수의 미분을 알아내고자 한다.

궤적 $\tau$ 는 $s_1,a_1,\dots ,s_T,a_T$ 를 의미하고 $r(\tau )$ 는 ${\sum }_{t=1}^{T}r(s_t,a_t)$ 를 의미한다.

$$J(\theta )=E_{\tau \sim p_{\theta }(\tau )}[r(\tau )]=\int p_{\theta }(\tau )r(\tau )d\tau$$

이를 미분할 것인데, 이 때 $f\nabla \log f=f\frac{\nabla f}{f}=\nabla f$ 임을 이용하여 수식을 전개한다.

$${\nabla }_{\theta }J(\theta )=\int {\nabla }_{\theta }{p}_{\theta }(\tau )r(\tau )d\tau =\int p_{\theta }(\tau ){\nabla }_{\theta }\log p_{\theta }(\tau )r(\tau )d\tau =E_{\tau \sim p_{\theta }(\tau )}[{\nabla }_{\theta }\log p_{\theta }(\tau )r(\tau )]$$

$\log p_{\theta }(\tau )$ 를 풀어내기 위해 궤적 확률분포 수식에 로그를 취해 구해본다.

$$p_{\theta }(s_1,a_1,\dots ,s_T,a_T)=p(s_1)\prod _{t=1}^T{\pi }_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t)$$ $$\log p_{\theta }(\tau )=\log p(s_1)+\sum _{t=1}^T\log {\pi }_{\theta }(a_t|s_t)+\log p(s_{t+1}|s_t,a_t)$$

그러면 이전에 목적함수를 풀어낼 수 있는데 $\theta$ 와 독립적인 요소들은 모두 0으로 바뀌므로 아래와 같이 정리된다.

$${\nabla }_{\theta }J(\theta )=E_{\tau \sim p_{\theta }(\tau )}[(\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t))(\sum _{t=1}^{T}r(s_t,a_t))]$$

Evaluating the policy gradient

앞서 목적함수를 샘플들의 평균으로 근사한 것처럼 미분도 표현할 수 있다.

$$J(\theta )=E_{\tau \sim p_{\theta }(\tau )}[\sum _{t}r(s_t,a_t)]\approx \frac{1}{N}\sum _i\sum _{t}r(s_{i,t},a_{i,t})$$ $${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N[(\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_{i,t}|s_{i,t}))(\sum _{t=1}^{T}r(s_{i,t},a_{i,t}))]$$

이를 이용해 $\theta$ 를 업데이트 한다. ($\theta \leftarrow \theta +\alpha {\nabla }_{\theta }J(\theta )$ )

이전 강의에서 다룬 알고리즘 개요도에서 주황색과 초록색 파트에 해당하는 수식을 잘 확인해보자.

이러한 방식이 REINFORCE 알고리즘으로 가장 기본적인 PG 알고리즘이다.

Part 2. Understanding Policy Gradients

$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N[(\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_{i,t}|s_{i,t}))(\sum _{t=1}^{T}r(s_{i,t},a_{i,t}))]$$

${\nabla }_{\theta }\log {\pi }_{\theta }(a_{i,t}|s_{i,t})$ 가 의미하는 바가 무엇일까?

강의 처음에 다루었던 이미지로 부터 취할 이산적인 행동(왼쪽 혹은 오른쪽)을 맵핑하는 policy 를 생각해보자.

그렇다면 $\log {\pi }_{\theta }(a_{i,t}|s_{i,t})$ 란 두 행동 중의 어떤 행동을 취할 지에 대한 로그 확률 분포이다.

Comparison to maximum likelihood

Supervised learning 에서는 $s_t,a_t$ 가 모두 주어진 학습 데이터로 모델을 학습시켜 ${\pi }_{\theta }(a_t|s_t)$ 를 얻는다.

그래서 supervised learning 에서의 목적함수의 미분은 아래와 같이 maximum likelihood 를 사용한다.

$${\nabla }_{\theta }{J}_{ML}(\theta )\approx \frac{1}{N}\sum _{i=1}^N(\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_{i,t}|s_{i,t}))$$

여기에서는 RL 과 다르게 행동이 좋은 행동이므로 그대로 사용하지만 RL 에서는 $a_{i,t}$ 가 좋은지 판단하기 위해 보상이라는 가중치를 두는 것으로 해석할 수 있다.

그래서 ML 에서는 모든 $a_{i,t}$ 에 대해 로그 확률을 증가시키지만 RL 에서는 보상에 따라 증가시키기도 하고 감소시키기도 한다.

Example: Gaussian policies

예제로 나온 policy ${\pi }_{\theta }(a_t|s_t)$ 는 연속적인 행동의 확률분포를 내는 것으로 신경망에서 내는 값을 평균으로 하는 multivariate gaussian distribution $\mathcal{N}(f_{\text{neural network}}(s_t);\sum )$이다.

이에 대한 로그 확률은 아래와 같이 표현된다.

$$\log {\pi }_{\theta }(a_t|s_t)=-\frac{1}{2}\Vert f(s_t)-a_t{\Vert }_{\sum }^2+\text{const}$$

이에 미분을 취하면 아래와 같이 된다.

$${\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)=-\frac{1}{2}\sum ^{-1}(f(s_t)-a_t)\frac{df}{d\theta }$$

실제로 적용할 때는 역전파를 통해 $\frac{df}{d\theta }$ 를 계산한다고 한다.

What did we just do?

Policy gradient 는 좋은 궤적 $\tau$ 는 더 많이 나올 수 있도록 하고, 안좋은 궤적은 덜 일어나도록 만들어 주는 것으로 어떻게 보면 “trial and error” 과정으로 볼 수 있다.

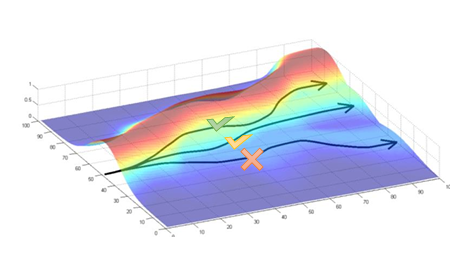
Partial observability

observation $o_t$ 가 있는 상황에서는 목적함수의 미분이 $s_t$ 대신 $o_t$ 가 들어간 수식으로 바뀐다.

$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N[(\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_{i,t}|o_{i,t}))(\sum _{t=1}^{T}r(s_{i,t},a_{i,t}))]$$

영상 설명에서는 Markov property 가 실제로 사용되지는 않아서, 별다른 변화없이 위와 같이 수식이 유도되고 그래서 큰 차이 없이 policy gradient 를 적용하면 된다고 한다.

What is wrong with the policy gradient?

하지만 실제로 policy gradient 를 적용해보면 그리 잘 작동하지 않는다.

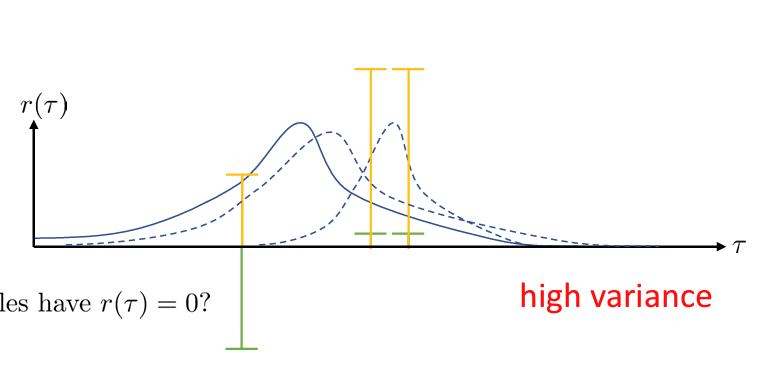
위 그래프에서 파란 선은 확률 분포를 의미하고, 초록, 노란색 바는 샘플의 보상값을 의미한다.

초록색의 보상값을 갖는 3개의 샘플 같은 경우에는 보상과 확률분포를 곱해 gradient 를 계산하므로 확률을 매우 낮추는 방향으로 확률 분포가 변할 것이다.

노란색의 보상값을 갖는 샘플들의 경우에는 모두 양수이므로 적절하게 변할 것이다.

그러므로 어떤 샘플을 얻느냐에 따라 보상값이 달라져 큰 분산값을 가지게 된다. (물론 샘플을 무한하게 가져가면 정확한 policy gradient 를 수행할 수 있다.== sample inefficiency)

그래서 RL 을 실제로 적용할 때는 분산을 낮추고자 한다.

The-Problem-With-Policy-Gradient

Part 3. Reducing Variance

이전의 policy gradient 에서는 특정 $t$ 일 때의 $\log \pi$ 의 gradient 에 $t=1,\dots ,T$ 까지의 모든 보상을 곱하였다.

Causality: $t^{\prime }$ 에서의 policy 는 $t<t^{\prime }$ 인 $t$ 에서의 policy 에 영향을 줄 수 없다.

$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N[(\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_{i,t}|o_{i,t}))(\sum _{t^{\prime }=t}^{T}r(s_{i,t^{\prime }},a_{i,t^{\prime }}))]$$

이렇게 하면 과거 시점의 보상은 더이상 확률 분포를 변화시키는데 영향을 미치지 못하고 $t$ 에서 취한 $a_t$ 로 인한 보상값만 곱하게 되어 덜 편향적이게 된다.

영상에서는 모든 horizon 에서의 보상값을 다 합하지 않고 특정 시점 이후의 값만 합하므로 기댓값이 작아지고 그래서 분산도 더 작아진다고 하였다. 이부분이 잘 이해가 가지 않았는데 두 가지로 나눠서 생각해볼 수 있을 것 같다.

우선, 이전 설명에서 분산이 컸던 이유는 랜덤하게 얻는 정해진 양의 샘플에 따라 달라지는 보상의 크기였는데 이를 전반적으로 작게 만들기 때문으로 볼 수 있다. (weight 관점에서의 $r$ 이 작아지므로)

또 하나는, 수식에 없는 discount factor $\gamma$ 이다. 기댓값이 작아진다고 분산이 작아지지는 않기 때문에 위의 설명이 타당하려면 시간에 따라 보상의 값이 작아져야 한다. 그렇다면 $t^{\prime }=1,\dots$ 가 아닌 $t^{\prime }=t,\dots ,T$ 부터 보상값을 합하였을 때 분산이 작아지는 것이 맞게 된다.

${\sum }_{t^{\prime }=t}^{T}r(s_{i,t^{\prime }},a_{i,t^{\prime }})$ 를 “reward-to-go” 로 부르고 ${\hat{Q}}_{i,t}$ 로 표기하기도 한다.

Baselines

Policy gradient 를 실제로 잘 작동하게 하기 위한 방법 중 하나로 “baseline” 도 있다.

우리가 이전에 살펴보았던 이러한 그림을 생각해보았을 때 아래와 같이 보상의 평균과 차이로 weight 를 주는 수식이 더 타당해보인다.

$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }\log p_{\theta }(\tau )[r(\tau )-\frac{1}{N}\sum _{i=1}^{N}r(\tau )]$$

왜냐하면 좋은 궤적은 (+)의 보상을 갖고 나쁜 궤적은 (-)의 보상을 갖는 것 맞아보이기 때문이다. 모든 궤적이 (+)의 보상을 갖고 서로 다른 크기일 뿐이라면 $\log \pi$ 의 gradient 의 weight 또한 모두 양수가 된다.

하지만 이렇게 하여도 상관이 없는 것일까?

실제로 보상의 평균 $b=\frac{1}{N}{\sum }_{i=1}^{N}r(\tau )$ 을 빼더라도(혹은 어떤 baseline $b$ 든지) $\log p_{\theta }$ 의 gradient 의 기댓값이나 분산을 변화시키지 않는다.

$$E[{\nabla }_{\theta }\log p_{\theta }(\tau )b]=\int p_{\theta }(\tau ){\nabla }_{\theta }\log p_{\theta }(\tau )bd\tau =\int {\nabla }_{\theta }{p}_{\theta }(\tau )bd\tau =b{\nabla }_{\theta }\int p_{\theta }(\tau )d\tau =b{\nabla }_{\theta }1=0$$

subtracting a baseline is unbiased in expectation. average reward is not the best base line, but it works well.

Analyzing variance

최적의 분산을 얻기 위한 $b$ 는 gradient 에 의존하게 된다. multivariate distribution 에서는 policy 의 변수 갯수에 따라 각각 다른 최적의 분산을 갖게 된다. (different baseline for every entry of gradient)

Part 4. Off-Policy Policy Gradients

Policy gradient 는 on-policy 알고리즘이다. 수식을 살펴보면 ${\nabla }_{\theta }J(\theta )=E_{\tau \sim p_{\theta }(\tau )}[{\nabla }_{\theta }\log p_{\theta }(\tau )r(\tau )]$ 에서 $\tau \sim p_{\theta }(\tau )$ 부분으로 인해 $\theta$ 가 바뀔 때마다 샘플링을 다시 수행해야 한다.

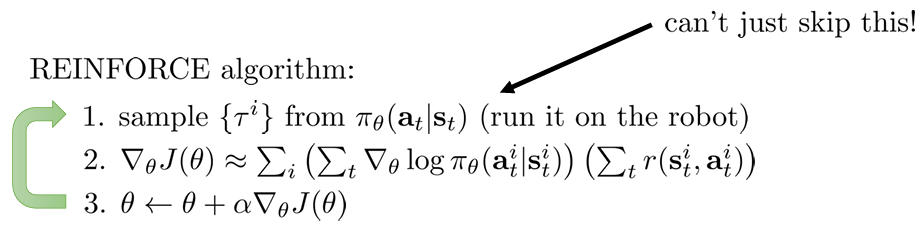
신경망에서는 각 gradient 마다 가중치가 매우 조금씩 변하기 때문에 이러한 on-policy 방식은 매우 비용이 높고, sample inefficient 하다.

Off-policy learning & importance sampling

만약 $p_{\theta }(\tau )$ 에서의 샘플이 없고 $\bar{p}$ 에서 얻은 샘플이 있다면(이전 policy 나 사람으로부터 직접 얻은) 어떡할까?

여기에서는 중요 샘플링을 통해 기댓값을 구한다. 중요 샘플링은 다른 확률 분포로부터 얻은 샘플로 구하고자 하는 확률 분포의 기댓값을 구하는 것이다.

Importance Sampling

$$E_{x\sim p(x)}[f(x)]=\int p(x)f(x)dx=\int \frac{q(x)}{q(x)}p(x)f(x)dx=\int q(x)\frac{p(x)}{q(x)}f(x)dx=E_{x\sim q(x)}[\frac{p(x)}{q(x)}f(x)]$$

이를 이용해 목적함수를 표현하면 아래와 같다.

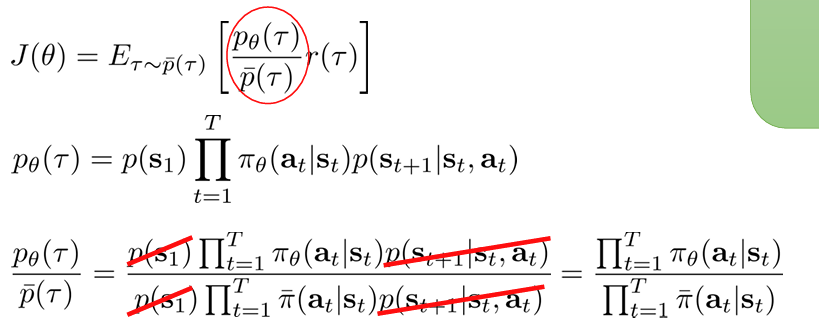
각 확률분포의 비는 policy 확률의 비로 간단하게 표현된다.

Deriving the policy gradient with Importance Sampling

이제 이를 이용해 policy gradient 수식을 유도해보자.

새로운 ${\theta }^{\prime }$ 에 대해서 $J({\theta }^{\prime })=E_{\tau \sim p_{\theta }(\tau )}[\frac{p_{{\theta }^{\prime }}(\tau )}{p_{\theta }(\tau )}r(\tau )]$ 를 미분하면 ${\theta }^{\prime }$ 와 관련된 부분만 미분을 취하면되고 이를 풀어내면 아래와 같다.

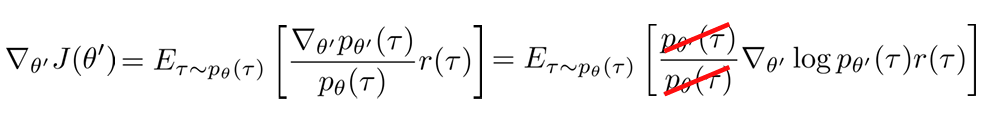
여기서 빨간색으로 지워진 부분은 $\theta ={\theta }^{\prime }$ 로 보는 경우 기존의 policy gradient 과 같다는 것을 보여주기 위해 슬라이드에서 표시된 것이다.

The off-policy policy gradient

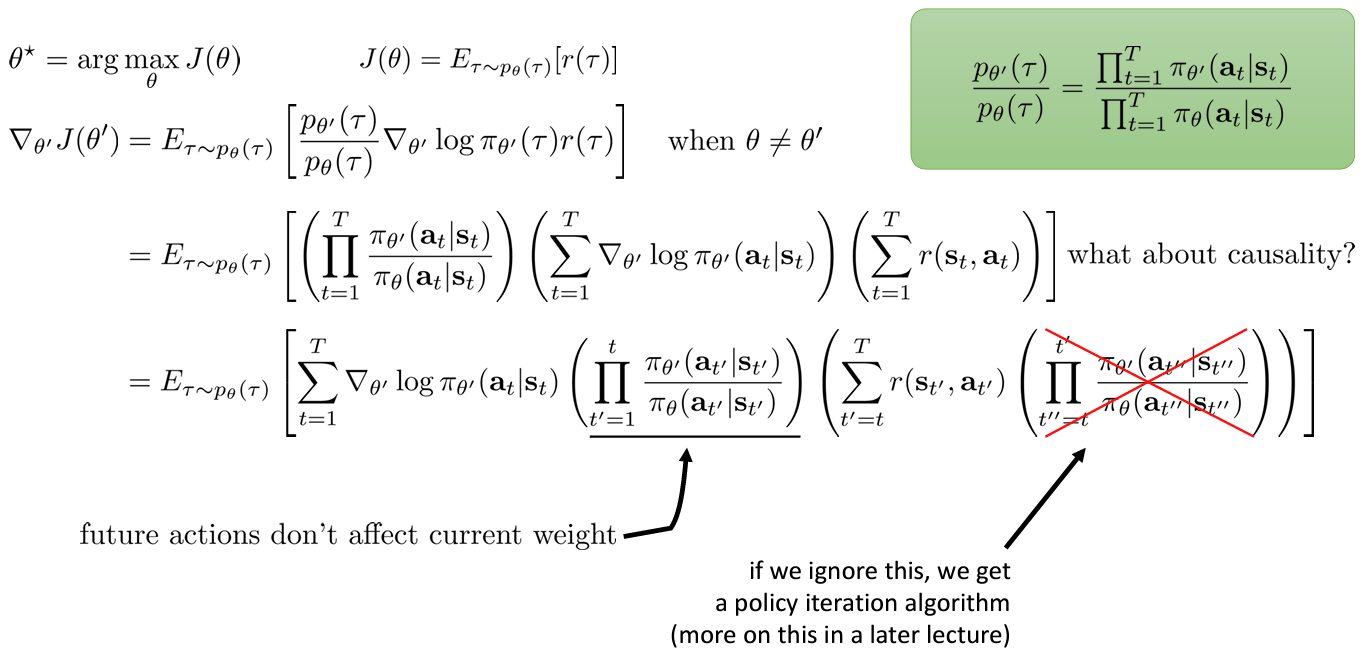
우리가 다루는 것은 $\theta \ne {\theta }^{\prime }$ 일 때이므로 수식 전개는 위와 같다. “reward-to-go” 에서 과거의 보상은 고려하지 않게 되면 최종적으로 마지막 줄과 같이 되지만 ${\prod }_{t^{\prime }=1}^t\frac{{\pi }_{{\theta }^{\prime }}(a_{t^{\prime }}|s_{t^{\prime }})}{{\pi }_{\theta }(a_{t^{\prime }}|s_{t^{\prime }})}$ 를 구하는 것이 문제가 된다.

A first-order approximation for IS

${\prod }_{t^{\prime }=1}^t\frac{{\pi }_{{\theta }^{\prime }}(a_{t^{\prime }}|s_{t^{\prime }})}{{\pi }_{\theta }(a_{t^{\prime }}|s_{t^{\prime }})}$ 가 문제인 이유는 $T$ 에 기하급수적으로 작아지기 때문이다. 이 값이 1보다 작게 되면 항을 곱할 수록 0에 가까워지고 이는 안그래도 큰 분산을 무한대로 크게 만드는 문제가 있다.

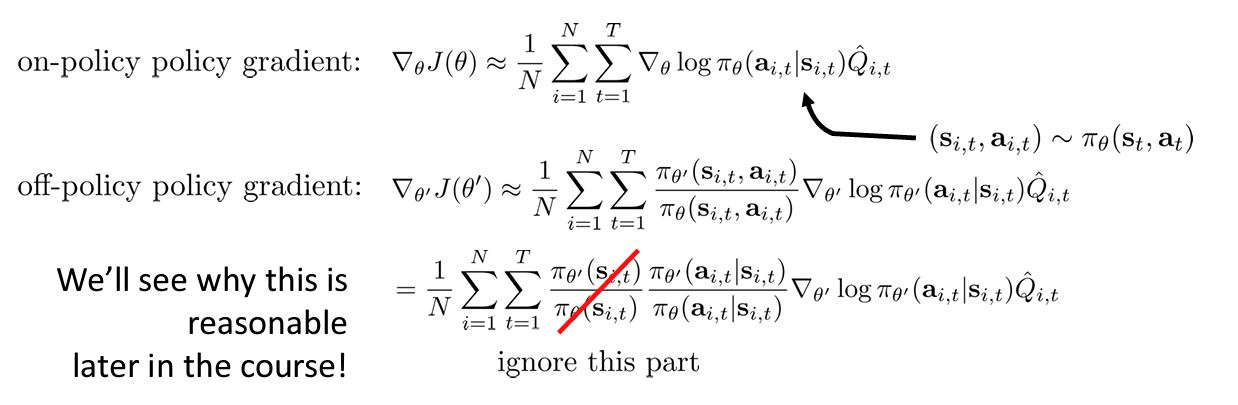
deriving-state-action-marginal-in-reinforcement-learning

그래서 위와 같이 state-action marginal 을 이용해 수식을 바꿔서 표현할 수 있다. 물론 초기의 state 확률 분포와 transition probability 를 알아야 구할 수 있지만, chain rule 을 이용해 분수를 분리하고 $\frac{{\pi }_{{\theta }^{\prime }}(s_{i,t})}{{\pi }_{\theta }(s_{i,t})}$ 를 무시하면 해당 $t$ 에서만 weight 만 곱하므로 기하급수적으로 증가하지 않는다.

Part 5. Implementing Policy Gradients

Policy gradient with automatic differentiation

텐서플로우나 파이토치를 이용해 policy gradient 를 수행함에 있어서 ${\nabla }_{\theta }\log {\pi }_{\theta }(a_{i,t}|s_{i,t})$ 를 계산하는 것이 매우 비효율적이다. 왜냐하면 신경망의 $\theta$ 가 샘플의 수보다 매우 많기 때문이다.

그래서 실제로 코드로 적용할 때는 weighted maximum likelihood 의 “pseudo-loss” 처럼 작성한다.

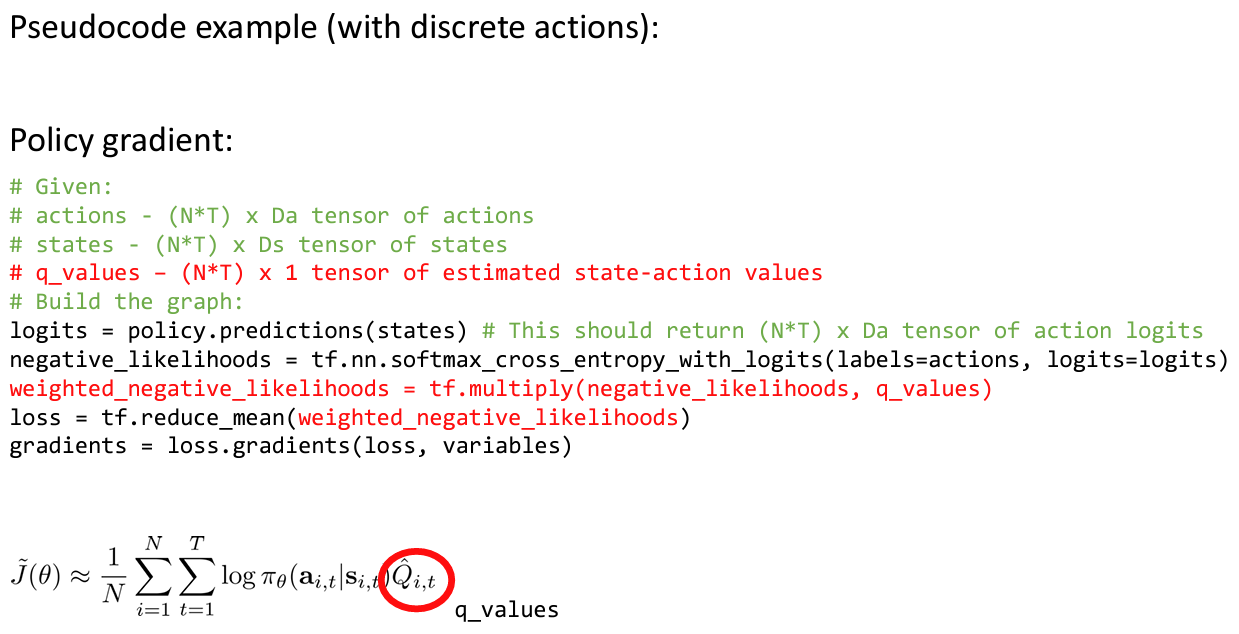
Policy gradient in practice

Part 6. Advanced Policy Gradients

What else is wrong with the policy gradient?

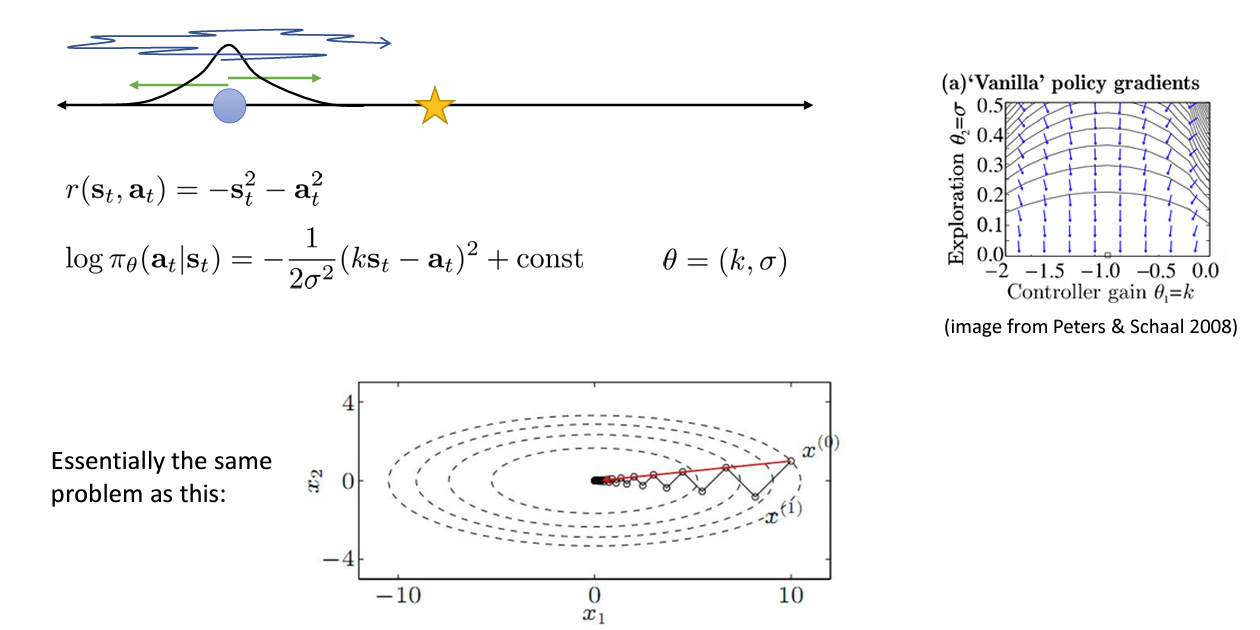
강의에서는 위와 같은 보상함수를 정의하고 로그 확률을 표현하였는데, 오른쪽의 vector field 그림을 살펴보면 optimum 인 (-1.0, 0.0) 으로 gradient(파란 화살표)가 나아가지 않는다는 것이다.

교수님의 설명에서는 $s(\sigma )$ 가 작아질 수록 $\sigma$ 에 대한 그 미분값은 커지기 때문이라고 하였다. (2분 30초대)

Gaussian probability 수식을 미분하면 $k$ 에 대한 미분보다 $\sigma$ 에 대한 미분의 영향이 더 커진다고 한다. (이 부분 설명 이해 못함. fourth term 이 어떤 의미인지 모르겠음. 미분하면 $\frac{1}{{\sigma }^3}$ 가 아닌가)

Covariant/natural policy gradient

$k,\sigma$ 에 모두 적절한 step size 를 선정하기 어렵다.

그래서 $\alpha$ 의 수학적인 의미로부터 policy 들의 divergence 에 대한 constraint 을 부여하도록 하고 이를 측정하는데에는 KL-divergence $D_{\text{KL}}$ 을 사용한다.

이렇게 하여 policy gradient 를 수행하면 이전보다 훨씬 좋은 vector field 를 얻을 수 있다.

Advanced policy gradient topics

• What more is there?
• Next time: introduce value functions and Q-functions
• Later in the class: more on natural gradient and automatic step size adjustment

Policy gradients suggested readings

• Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach Learn 8, 229–256 (1992). https://doi.org/10.1007/BF00992696
• Baxter, Jonathan, and Peter L. Bartlett. “Infinite-horizon policy-gradient estimation.” journal of artificial intelligence research 15 (2001): 319-350. https://doi.org/10.48550/arXiv.1106.0665
• Jan Peters, Stefan Schaal, Reinforcement learning of motor skills with policy gradients, Neural Networks, Volume 21, Issue 4, 2008, Pages 682-697, ISSN 0893-6080, https://doi.org/10.1016/j.neunet.2008.02.003.
• Levine, S. & Koltun, V.. (2013). Guided Policy Search. Proceedings of the 30th International Conference on Machine Learning, in Proceedings of Machine Learning Research 28(3):1-9 Available from https://proceedings.mlr.press/v28/levine13.html.
• Schulman, John, et al. “Trust region policy optimization.” International conference on machine learning. PMLR, 2015. https://doi.org/10.48550/arXiv.1502.05477
• Schulman, John, et al. “Proximal policy optimization algorithms.” arXiv preprint arXiv:1707.06347 (2017). https://doi.org/10.48550/arXiv.1707.06347