Quasi-Newton & BFGS & L-BFGS

Quasi-Newton §

Quasi-Newton method 란 무엇일까? 위키피디아 를 바탕으로 간단히 살펴보고, 어떤 알고리즘들이 주로 사용되는지와 장단점을 알아보자.

Quasi-Newton methods §

Quasi-Newton method 란 목적함수의 영점이나 극소/극대값을 찾기 위한 방법이다.

Newton’s method 는 Jacobian 이나 Hessian 이 있어야 영점이나 극값을 찾을 수 있다. 반면 Quasi-Newton method 는 이러한 Jacobian 이나 Hessian 을 사용할 수 없거나 매번 계산하기 매우 어려운 경우에 사용할 수 있다.

Search for zeros: root finding §

위에서 말한 영점을 찾는 다는 것은 목적함수의 해를 구하는 것이다.

Newton’s method 에서는 $x_n$ 에서의 Jacobian $J_g(x_n)$ 의 left inverse $[J_g(x_n){]}^{-1}$ 에 대해 아래와 같다.

$$x_{n+1}=x_n-[J_g(x_n){]}^{-1}g(x_n)$$

여기서 목적함수 $g$ 는 다변수 함수이다.

여기에서 $J_g(x_n)$ 를 대체해서 푸는 모든 방법들이 quasi-Newton method 에 속한다.

대개 극값을 찾기 위한 방법은 대칭인 행렬을 필요로 해서 이러한 방법들을 해를 찾는데 사용하는 것은 좋지 않다고 한다.

Search for extrema: optimization §

Gradient 의 해를 구한다는 것은 원래 함수의 극값을 찾는 것과 같으므로 quasi-Newton method 는 극값을 찾는데 사용될 수 있다. 즉, $g$ 가 $f$ 의 gradient 라면 $g$ 의 Jacobian 은 $f$ 의 Hessian 이 된다.

이렇게 찾은 극값은 목적함수의 local maxima and minima 가 된다.

Newton method expansion §

Newton method 에서는 최적해 근처에서 수식을 이차 테일러 급수식으로 근사화하고 일, 이차 도함수를 통해 최적해를 찾는다.

$$f(x_k+t)\approx f(x_k)+f^{\prime }(x_k)t+\frac{1}{2}{f}^{\prime \prime }(x_k)t^2$$

이 때 $f:\mathbb{R}\to \mathbb{R}$ 는 이계도함수를 갖고 초기값 $x_0\in \mathbb{R}$ 에서 ${\min }_{x\in \mathbb{R}}f(x)$ 인 $x^{\ast }$ 를 찾고자 한다.

iteration 을 통해 $x_0$ 부터 $x^{\ast }$ 까지의 $\{x_k\}$ 를 찾고자 $x_{k+1}=x_k+t$ 로 두면 위의 근사식을 미분하여 $t$ 를 찾을 수 있다.

$$0=\frac{d}{dt}(f(x_k)+f^{\prime }(x_k)t+\frac{1}{2}{f}^{\prime \prime }(x_k)t^2)=f^{\prime }(x_k)+f^{\prime \prime }(x_k)t$$

Note

• 위의 이차 근사식이 이러한 미분을 통해 최솟값을 찾는 것이 보장되려면 함수 $f$ 가 convex 해야 한다.
• 즉, $f^{\prime \prime }>0$ 이어야 한다.

따라서 식을 정리해보면 아래와 같다.

$$x_{k+1}=x_k+t=x_k-\frac{f^{\prime }(x_k)}{f^{\prime \prime }(x_k)}$$

더 높은 차원에서는 이차 도함수의 Hessian $H_f(x)={\nabla }^{2}f(x)\in {\mathbb{R}}^{d\times d}$ 을 사용하는데, quasi-Newton 에서는 이를 필요로하지 않는다.

$$x_{k+1}=x_k-\frac{\nabla f(x)}{{\nabla }^{2}f(x)}$$

대신 연속적인 gradient 를 통해 Hessian 을 업데이트한다.

Quasi-Newton method expansion §

Quasi-Newton methods 는 secant method 의 방법을 일반화 한것으로 고차원에서는 secant equation 이 under-determined 이므로, 이를 어떤 제약조건을 통해 해를 구하는지에 따라 달라진다. (보통은 Hessian 의 현재 추정치에 간단한 low-rank 업데이트를 통해 이루어진다.)

가장 많이 사용되는 quasi-Newton 알고리즘은 SR1 formula, BHHH method, BFGS method 와 적은 메모리를 사용하는 L-BFGS 가 있다.

그 중, SR1 fomula 는 업데이트하는 행렬의 positive-definiteness 를 보장하지 못해서 indefinite problem 에 사용된다.

Quasi-Newton method 가 Newton method 보다 갖는 큰 장점 중 하나는 Hessian $B$ 의 역행렬을 구할 필요가 없다는 것이다. 대신 $B^{-1}$ 의 근사를 직접 만들어 사용한다.

Newton method expansion 처럼 이차 테일러 급수로 목적함수 $f(x)$ 를 표현해보자.

$$f(x_k+\Delta x)\approx f(x_k)+\nabla f(x_k{)}^T\Delta x+\frac{1}{2}\Delta x^{T}B\Delta x$$

이 때 $\nabla f$ 는 gradient 이고 $B$ 는 approximation to the Hessian matrix 이다.

이를 미분한 값이 0 이라고 하면 Newton step $\Delta x$ 를 구할 수 있고, 수식은 아래와 같다.

$$\nabla f(x_k+\Delta x)\approx \nabla f(x_k)+B\Delta x$$

$$\Delta x=-B^{-1}\nabla f(x_k)$$

Hessian 의 근사인 $B$ 은 secant equation 인 $\nabla f(x_k+\Delta x)=\nabla f(x_k)+B\Delta x$ 를 만족해야 한다. 이는 gradient $\nabla f$ 의 일차 테일러 근사와 같다.

주로 초기값 $B_0$ 는 $B_0=\beta I$ 로 사용하고 빠른 수렴에 충분하다. $B_0$ 는 positive-defininte 해야 한다.

그리고 현재 추정한 Hessian 행렬 $B_k$ 를 이용해 아래와 같이 다음 $x_k$ 를 업데이트 한다.

• $\Delta x_k=-{\alpha }_k{B}_k^{-1}\nabla f(x_k)$, $\alpha$ 는 Wolfe condition 만족하도록 한다.
• $x_{k+1}=x_k+\Delta x_k$
• 이를 이용해 $y_k=\nabla f(x_{k+1})-\nabla f(x_k)$ 를 수행한다.

위에서 구한 값들은 approximate Hessian $B_{k+1}$ 를 업데이트하거나 역행렬 $H_{k+1}=B_{k+1}^{-1}$ 을 구하기 위해 다시 사용된다.

많이 사용되는 업데이트 방식은 아래 표와 같다.

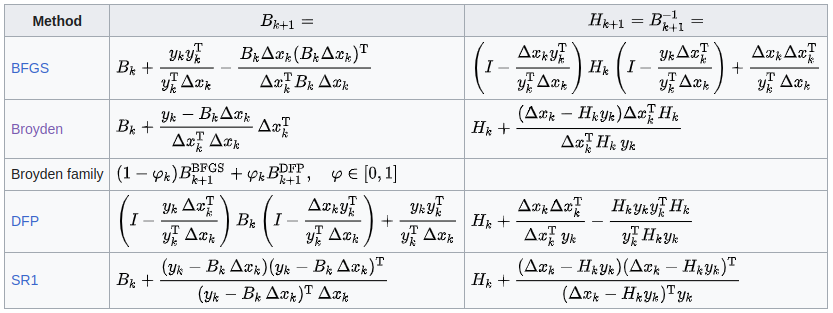
BFGS §

BFGS 알고리즘은 Broyden-Fletcher-Goldfarb-Shanno 의 약자로 unconstrained nonlinear optimization porblem 을 iterative 하게 풀어내는 방법으로 주로 사용된다.

BFGS 알고리즘은 gradient evaluation 로 얻은 Hessian 의 loss function 을 점진적으로 개선하면서 curvature 정보로 gradient descent 의 방향을 결정한다.

BFGS 의 curvature 행렬을 업데이트하는데 역행렬이 필요하지 않아 복잡도는 $\mathcal{O}(n^2)$ 이다. (Newton’s method 는 $\mathcal{O}(n^3)$ 이다.)

Rationale §

$\min f(\mathbf{x})\forall \mathbf{x}\in {\mathbb{R}}^n$ 이고 미분가능한 $f$인 최적화 문제가 있다.

초기값 ${\mathbf{x}}_0$ 으로부터 최적해를 구하기 위해 매번 반복적을 업데이트해간다.

Search direction (or descent direction) ${\mathbf{p}}_k$ 는 $k$ 번째에서 추정한 Hessian 행렬 $B_k$ 에 대해 아래와 같이 표현된다.

$$B_k{\mathbf{p}}_k=-\nabla f({\mathbf{x}}_k)$$

이는 위에서 다룬 Newton equation 의 수식 $\Delta x_k=-{\alpha }_k{B}_k^{-1}\nabla f(x_k)$ 에서 유도되었다.

그리고 이 때의 ${\mathbf{p}}_k$ 는 $f({\mathbf{x}}_k+\gamma \mathbf{p}k)$ 를 풀어내 다음 ${\mathbf{x}}_{k+1}$ 을 찾는데 사용된다.

$B_k$ 를 업데이트 할 때 사용되는 secant equation 은 $y_k=\nabla f(x_{k+1})-\nabla f(x_k)$ 와 $s_k=x_{k+1}-x_k$ 에 대해 아래와 같이 표현할 수 있다.

$$B_{k+1}{\mathbf{s}}_k={\mathbf{y}}_k$$

그리고 $B_{k+1}$ 이 positive definite 하도록 곡률 조건 ${\mathbf{s}}_k^T{\mathbf{y}}_k>0$ 을 만족해야 한다. ($i.e{s}_k^T{B}_{k+1}{s}_k=s_k^T{y}_k>0$)

$B_{k+1}$ 을 완전히 계산하는 대신 $B_k$ 에 두 행렬을 더해 구할 수 있다.

$$B_{k+1}=B_k+U_k+V_k$$

이 $U_k$ 와 $V_k$ 는 symmetric rank-one matrices 이고 그들의 합은 rank-two update matrix 이어야 한다.

따라서 BFGS 와 DFP 의 업데이트된 행렬은 이전 행렬에 rank-two 행렬만큼 달라진다.

$B_{k+1}$ 의 symmetry 와 positive definiteness 를 유지하기 위해 $B_{k+1}{\mathbf{s}}_k={\mathbf{y}}_k$ 로부터 $\mathbf{u}={\mathbf{y}}_k$ 와 $\mathbf{v}=B_k{\mathbf{s}}_k$ 를 골라 아래와 같이 업데이트를 정할 수 있다.

$$\begin{array}{rl}{B}_{k+1}& =B_k+\alpha \mathbf{u}{\mathbf{u}}^T+\beta \mathbf{v}{\mathbf{v}}^T\\ \text{s.t.}\alpha & =\frac{1}{{\mathbf{y}}_k^T{\mathbf{s}}_k},\beta =-\frac{1}{{\mathbf{s}}_k^T{B}_k{\mathbf{s}}_k}\\ \mathbf{u}& ={\mathbf{y}}_k,\mathbf{v}=B_k{\mathbf{s}}_k\end{array}$$

Algorithm §

Rationale를 바탕으로 전체 알고리즘과 역행렬 근사하는 부분까지 정리해보자.

풀어내려는 unconstrained optimization problem는 다음과 같다.

$$\underset{x\in {\mathbb{R}}^n}{\min }f(x)\text{where}f:{\mathbb{R}}^n\to \mathbb{R}$$

초기 추정값 $x_0\in {\mathbb{R}}^n$ 과 Hessian 의 초기 추정값 $B_0\in {\mathbb{R}}^{n\times n}$, 어떤 $ϵ>0$ 로부터 수렴할 때($i.e\Vert \nabla f({\mathbf{x}}_k)\Vert \le ϵ$) 까지 아래 단계를 반복한다.

Algorithm

1. $B_k{\mathbf{p}}_k=-\nabla f({\mathbf{x}}_k)$ 를 풀어 ${\mathbf{p}}_k$ 를 구한다.
2. Line search 를 통해 적절한 step size ${\alpha }_k$ 를 찾는다. $a_k=\arg \min f({\mathbf{x}}_k+\alpha {\mathbf{p}}_k)$ 로 구하거나 Wolfe condition 을 만족하는 ${\alpha }_k$ 를 찾는다.
3. ${\mathbf{x}}_{k+1}$ 을 구한다. ${\mathbf{x}}_{k+1}={\mathbf{x}}_k+{\mathbf{s}}_{k}s.t.{\mathbf{s}}_k=\alpha {\mathbf{p}}_k$
4. $y_k=\nabla f(x_{k+1})-\nabla f(x_k)$
5. $B_{k+1}=B_k+\frac{{\mathbf{y}}_k{\mathbf{y}}_k^T}{{\mathbf{y}}_k^T{\mathbf{s}}_k}-\frac{B_k{\mathbf{s}}_k{\mathbf{s}}_k^T{B}_k^T}{{\mathbf{s}}_k^T{B}_k{\mathbf{s}}_k}$

알고리즘의 첫 번째 step 에서 필요한 $B_k$ 의 역행렬은 5번째 스텝에 Sherman-Morrison formula 을 적용하여 매우 효과적으로 구할 수 있다.

$$B_{k+1}^{-1}=\left(I-\frac{{\mathbf{s}}_k{\mathbf{y}}_k^T}{{\mathbf{y}}_k^T{\mathbf{s}}_k}\right)B_k^{-1}\left(I-\frac{{\mathbf{y}}_k{\mathbf{s}}_k^T}{{\mathbf{y}}_k^T{\mathbf{s}}_k}\right)+\frac{{\mathbf{s}}_k{\mathbf{s}}_k^T}{{\mathbf{y}}_k^T{\mathbf{s}}_k}$$

이는 아래와 같은 전개를 통해 효율적으로 풀어진다. $B_k^{-1}$ 이 대칭행렬이고 ${\mathbf{y}}_k^{\mathrm{T}}{B}_k^{-1}{\mathbf{y}}_k$ 와 ${\mathbf{s}}_k^{\mathrm{T}}{\mathbf{y}}_k$ 이 스칼라임을 이용한다.

$$B_{k+1}^{-1}=B_k^{-1}+\frac{({\mathbf{s}}_k^{\mathrm{T}}{\mathbf{y}}_k+{\mathbf{y}}_k^{\mathrm{T}}{B}_k^{-1}{\mathbf{y}}_k)({\mathbf{s}}_k{\mathbf{s}}_k^{\mathrm{T}})}{({\mathbf{s}}_k^{\mathrm{T}}{\mathbf{y}}_k{)}^2}-\frac{B_k^{-1}{\mathbf{y}}_k{\mathbf{s}}_k^{\mathrm{T}}+{\mathbf{s}}_k{\mathbf{y}}_k^{\mathrm{T}}{B}_k^{-1}}{{\mathbf{s}}_k^{\mathrm{T}}{\mathbf{y}}_k}$$

따라서 Hessian 행렬을 그대로 이용하지 않고 역행렬을 구할 수 있다.: $H_k\stackrel{\mathrm{def}}{=}{B}_k^{-1}.$

초기 추정값 $x_0\in {\mathbb{R}}^n$ 과 Hessian 역행렬 $H_0\in {\mathbb{R}}^{n\times n}$ 을 가지고 수렴할 때 까지 아래 단계를 반복하여 수행한다.

Algorithm

1. $B_k{\mathbf{p}}_k=-\nabla f({\mathbf{x}}_k)$ 를 풀어 ${\mathbf{p}}_k$ 를 구한다.
2. Line search 를 통해 적절한 step size ${\alpha }_k$ 를 찾는다. $a_k=\arg \min f({\mathbf{x}}_k+\alpha {\mathbf{p}}_k)$ 로 구하거나 Wolfe condition 을 만족하는 ${\alpha }_k$ 를 찾는다.
3. ${\mathbf{x}}_{k+1}$ 을 구한다. ${\mathbf{x}}_{k+1}={\mathbf{x}}_k+{\mathbf{s}}_{k}s.t.{\mathbf{s}}_k=\alpha {\mathbf{p}}_k$
4. $y_k=\nabla f(x_{k+1})-\nabla f(x_k)$
5. $H_{k+1}=H_k+\frac{({\mathbf{s}}_k^{\mathrm{T}}{\mathbf{y}}_k+{\mathbf{y}}_k^{\mathrm{T}}{B}_k^{-1}{\mathbf{y}}_k)({\mathbf{s}}_k{\mathbf{s}}_k^{\mathrm{T}})}{({\mathbf{s}}_k^{\mathrm{T}}{\mathbf{y}}_k{)}^2}-\frac{B_k^{-1}{\mathbf{y}}_k{\mathbf{s}}_k^{\mathrm{T}}+{\mathbf{s}}_k{\mathbf{y}}_k^{\mathrm{T}}{B}_k^{-1}}{{\mathbf{s}}_k^{\mathrm{T}}{\mathbf{y}}_k}$.

Further developments §

BFGS 업데이트는 ${\mathbf{s}}_k^T{\mathbf{y}}_k>0$ 가 완전히 양수인 조건에 크게 의존한다. 이는 convex target 에 대해 Wolfe condition 을 만족하며 line search 를 수행해야 하는데, Sequential Quadratic Programming 같은 경우에서는 음수나 거의 0에 가까운 곡률을 얻기도 한다.

따라서, 이러한 경우에는 ${\mathbf{s}}_k$ 나 ${\mathbf{y}}_k$ 를 적절히 변경하는 damped BFGS 라고 불리는 업데이트를 수행하기도 한다.

Limited-memory BFGS §

L-BFGS 는 앞서 다룬 BFGS 에 제한된 메모리를 사용하는 방법이다.

앞선 알고리즘은 거의 동일하지만 BFGS 는 dense 한 $n\times n$ 크기의 Hessian 역행렬을 저장하고 있는 반면, L-BFGS 는 몇 개의 vector 만 저장한다.

이 때의 $n$ 은 풀어내야 하는 문제의 변수의 갯수이므로 많은 변수를 가지고 있는 최적화 문제를 풀어낼 때 L-BFGS 가 적합한 방법이다.

L-BFGS 는 $H_k$ 를 모두 저장하는 대신 지난 $m<10$ 개의 업데이트에서의 $x$ 와 $\nabla f(x)$ 를 저장한다.

Algorithm §

L-BFGS 는 다른 quasi-Newton 방식과 매우 비슷하지만 approximate Newton’s direction 인 $d_k$ 와 현재 gradient $g_k$, Hessian 역행렬 $H_k$에 대해 matrix-vector multiplication $d_k=-H_k{g}_k$ 를 수행한다는 점에서 차이가 있다.

이전 update 를 이용해 이 $d_k$ 를 구하는 여러 연구들이 진행되었지만 가장 널리 사용되는 방법은 “two-loop recursion 이다.

주어진$x_k$ 와 $g_k\equiv \nabla f(x_k)$ 에 대해 아래 $s_k,y_k$ 를 지난 $m$ 업데이트 동안 갖고 있다고 가정한다.

$$\begin{array}{rl}{s}_k& =x_{k+1}-x_k\\ y_k& =g_{k+1}-g_k\end{array}$$

이를 가지고 ${\rho }_k=\frac{1}{y_k^{\top }{s}_k}$ 를 구한다.

그리고 $k$ 번 째에서 초기 Hessian 역행렬을 $H_k^0$ 이라고 한다. 위 BFGS 에서 정리한 역행렬 계산을 ${\rho }_k$ 로 정리하면 아래와 같다.

$$H_{k+1}=(I-{\rho }_k{s}_k{y}_k^T)H_k(I-{\rho }_k{y}_k{s}_k^T)+{\rho }_k{s}_k{s}_k^T$$

고정된 $k$에 대해 벡터의 수열 $q_{k-m},\dots ,q_k$을 $q_k:=g_k$ 와 $q_i:=(I-{\rho }_i{y}_i{s}_i^{\top })q_{i+1}$ 로 정의한다.

그리고 $q_{i+1}$로부터 $q_i$를 계산하기 위한 재귀적 알고리즘을 ${\alpha }_i:={\rho }_i{s}_i^{\top }{q}_{i+1}$ 를 이용해 $q_i=q_{i+1}-{\alpha }_i{y}_i$로 설정한다.

또 다른 벡터의 수열 $z_{k-m},\dots ,z_k$을 $z_i:=H_i{q}_i$로 정의하면 이 벡터들을 계산하기 위한 또 다른 재귀적 알고리즘은 $z_{k-m}=H_k^0{q}_{k-m}$ 로부터 시작하여 ${\beta }_i:={\rho }_i{y}_i^{\top }{z}_i$와 $z_{i+1}=z_i+({\alpha }_i-{\beta }_i)s_i$ 를 재귀적으로 푸는 것으로 정의한다.

그러면 $z_k$ 값은 ascent direction 이 되고 이를 이용해 descent direction 을 다음과 같이 계산할 수 있다:

$$\begin{array}{l}q=g_k\\ \mathtt{For}i=k-1,k-2,\dots ,k-m\\ {\alpha }_i={\rho }_i{s}_i^{\top }q\\ q=q-{\alpha }_i{y}_i\\ {\gamma }_k=\frac{s_{k-1}^{\top }{y}_{k-1}}{y_{k-1}^{\top }{y}_{k-1}}\\ H_k^0={\gamma }_{k}I\\ z=H_k^{0}q\\ \mathtt{For}i=k-m,k-m+1,\dots ,k-1\\ {\beta }_i={\rho }_i{y}_i^{\top }z\\ z=z+s_i({\alpha }_i-{\beta }_i)\\ z=-z\end{array}$$

즉, $q_{k-1}$ 부터 구해낸 $q_{k-m}$ 까지 구해낸 후에 이를 이용해 다시 $z_i$ 를 구한다.

그렇게 하면 앞서 언급한 approximate Newton’s direction 인 $d_k(=z_k)$ 를 얻게 된다.

$m=2$ 일 때 자세히 유도과정을 설명한 포스트가 Derivation of LBFGS 에 있으니 참고하면 좋다.

초기 행렬 ${\gamma }_k$의 scaling 은 검색 방향이 잘 scaling되어 있음을 보장하여 대부분의 iteration 에서의 unit step length 가 수용된다.

Wolfe line search 를 통해 곡률 조건 $y_k^{\top }{s}_k>0$ 이 만족되고 안정적인 BFGS 업데이트를 보장한다. 일부 소프트웨어 구현에서는 Armijo backtracking line search 를 사용하지만, 선택된 step 으로 인해 곡률 조건 $y_k^{\top }{s}_k>0$이 만족되는 것을 보장할 수 없다.

일부 구현에서는 $y_k^{\top }{s}_k$가 음수이거나 너무 0에 가까울 때 BFGS 업데이트를 건너뛰어 처리하기도 한다. 그러나 이 방법은 Hessian 근사치 $H_k$가 중요한 곡률 정보를 포착할 수 있도록 업데이트를 너무 자주 건너뛰게 될 수 있다. BFGS 에서 언급한대로 일부 sover 는 곡률 조건을 만족시키기 위해 $s_k$와 $y_k$를 수정하는 damped (L)BFGS 업데이트를 사용한다.

two-loop recursion 방식은 Hessian 의 역행렬을 곱셈하는 효율성 때문에 unconstrained optimization 에 널리 사용된다고 한다. 이 외의 접근 방식으로 Hessian 이나 그 역행렬의 low-rank 표현을 사용하는 것도 있다고 한다. 이는 Hessian 을 diagonal 행렬과 low-rank 업데이트의 합으로 나타내는 것으로 SQP 와 같은 constrained problem 에서 L-BFGS 를 사용할 수 있도록 해준다.

L-BFGS-B §

L-BFGS 의 파생 중에 관심갔던 알고리즘은 L-BFGS-B 이다. 왜냐하면 L-BFGS 간단한 bound constraints ($i.e{l}_i\le x_i\le u_i$)를 다룰 수 있도록 한 알고리즘이기 때문이다.

Comparison with Other Solvers §

여타 많은 알고리즘들과 차이가 궁금하였다. 예를 들어, 딥러닝에서는 Adam optimizer 를 대개 사용하는데 이러한 방식과 BFGS 방식과의 차이점을 찾아보았다.

L-BFGS vs Adam §

https://stats.stackexchange.com/questions/315626/the-reason-of-superiority-of-limited-memory-bfgs-over-adam-solver

ADAM 은 모든 dimension 에서 step size 를 조정하는 first order 방법이다. 어떤 의미에서는 이것은 모든 단계에서 diagonal Hessian 을 구성하는 것과 비슷하지만, 단순히 과거의 gradient 를 사용하여 수행한다. 이런 식으로 하면 여전히 first order 방법이지만 second order 방법인 것처럼 작동하는 이점이 있다.

각 차원을 따라만 추정하고 Hessian 에서 대각선을 벗어난 부분을 고려하지 않는다는 점에서 L-BFGS 보다 더 부족한 추정치이다. Hessian 이 거의 singular 하면 diagonal 을 벗어난 부분이 곡률에 중요한 역할을 할 수 있으며 이러한 경우 ADAM 은 BFGS 에 비해 성능이 저하될 가능성이 높다.

Benchmark §

여러 quasi-Newton method 혹은 다른 gradient descent 와 같은 알고리즘들 중에서 어떠한 것이 우수한지, 혹은 unconstrained optimization 에서 가장 적절한지 궁금하였다.

우선 Mantid 라는 데이터 사이언스에서 사용하는 라이브러리에서 제시된 비교가 있었다.

자세한 알고리즘의 종류와 풀어낸 문제는 사이트 를 참고하자.

Nonlinear regression problem 을 풀었는데 정확도와 런타임에 대해 아래와 같이 결과가 나왔다.

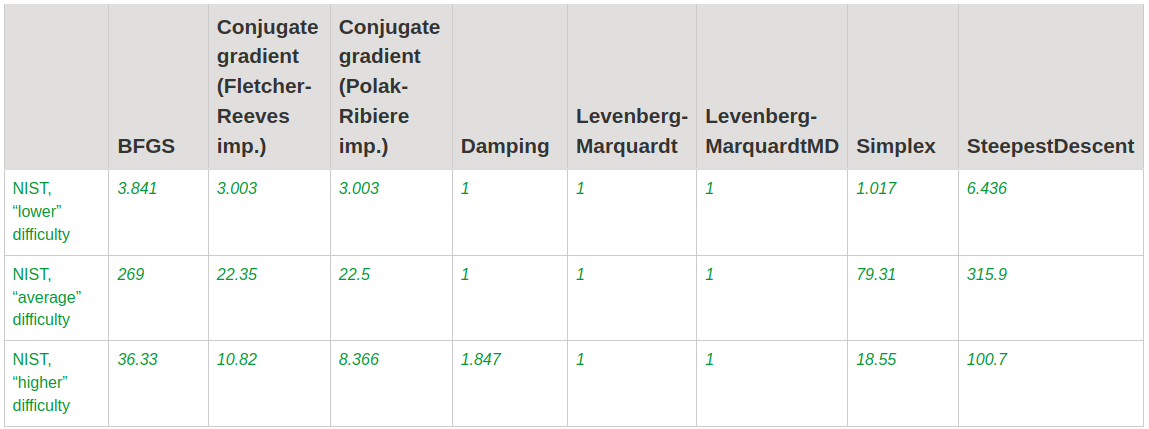
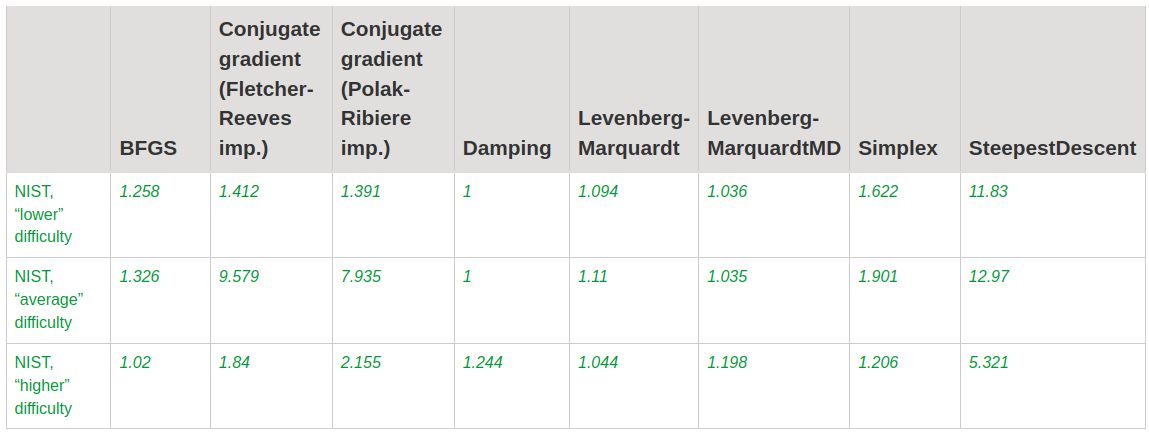
보다시피 SLAM 분야에서 least-square 를 구하기 위해 사용되는 Levenberg-Marquardt 나 Damping 방식이 전반적으로 우수하였고, 그 뒤이어 Simplex 나 BFGS 가 있었다. L-BFGS 에 대해서는 다뤄지지 않기는 하였으나 BFGS 가 좋지 않은 이유는 풀어내는 문제가 regression 이었기 때문으로 보인다.

References

• Quasi-Newton method
• BFGS
• Limited-memory BFGS
• Mantid: Benchmarks
• Derivation of LBFGS