[Aerial Robotics] Introduction

Robotics: Aerial Robotics

cousera 에 오픈 강의로 열려 있는 Robotics: Aerial Robotics 를 이번 달 동안 수강해보려고 한다.

강의는 Vijay Kumar 교수님이 진행하신다. 드론 분야에서 유명하시고 최근에는 Multi-robot 이나 실제 Application 쪽으로 확장해서 연구 중이신 것으로 보인다.

목차는

1. Introduction to Aerial Robotics
2. Geometry and Mechanics
3. Planning and Control
4. Advanced Topics

로 이루어져 있고, MATLAB 으로 실습을 진행한다.

강의가 꽤 옛날에 촬영된 것으로 보인다.

이번 포스트에서는 1강 Introduction to Aerial Robotics 를 정리한다.

대부분 기초 내용이 많아서 불필요한 내용들은 생략.

Introduction

Unmanned Aerial Vehicles

이 강의에서는 UAVs = RPVs = Aerial Robots = Drones 로 용어를 통일하였다.

RPV(Remotely Piloted Vehicle)은 주로 공군에서 사용하는 원격조종으로 기동하는 무인기이다.

무인기의 종류에는 아래 사진과 같이 군용 무인기부터 소형 DIY 기체까지 크기와 무게가 다양하다.

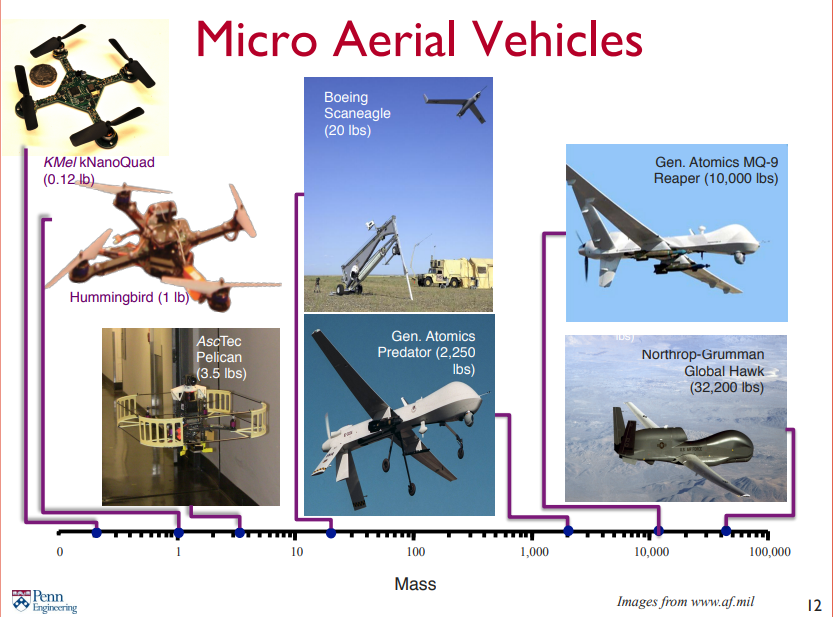
Drone 은 Fixed wing(고정익), Flapping wing(날개치기), Rotor crafts(회전익) 으로 분류할 수 있다. 그렇기에 다양한 형태를 가지고, 필요에 맞게 설계할 수 있다.

각각에는 장단점이 있다. 고정익의 경우 한 자리에서 hover 할 수 없는 단점이 있다.

Flapping wing의 형태는 실제 새의 날갯짓을 형상화하고자 한 기체이다. 그러나, 유체역학 문제를 해결하기 어렵기 때문에 이를 적절하게 모델링하고 제어하기 어렵다.

반면 회전익인 쿼드/헥사로터의 경우에는 상당히 단순한 형태의 모델이기 때문에 이동과 회전을 제어하기 간편하다.

이번 강의에서는 쿼드로터를 기준으로 설명이 이루어진다.

Quadrotors

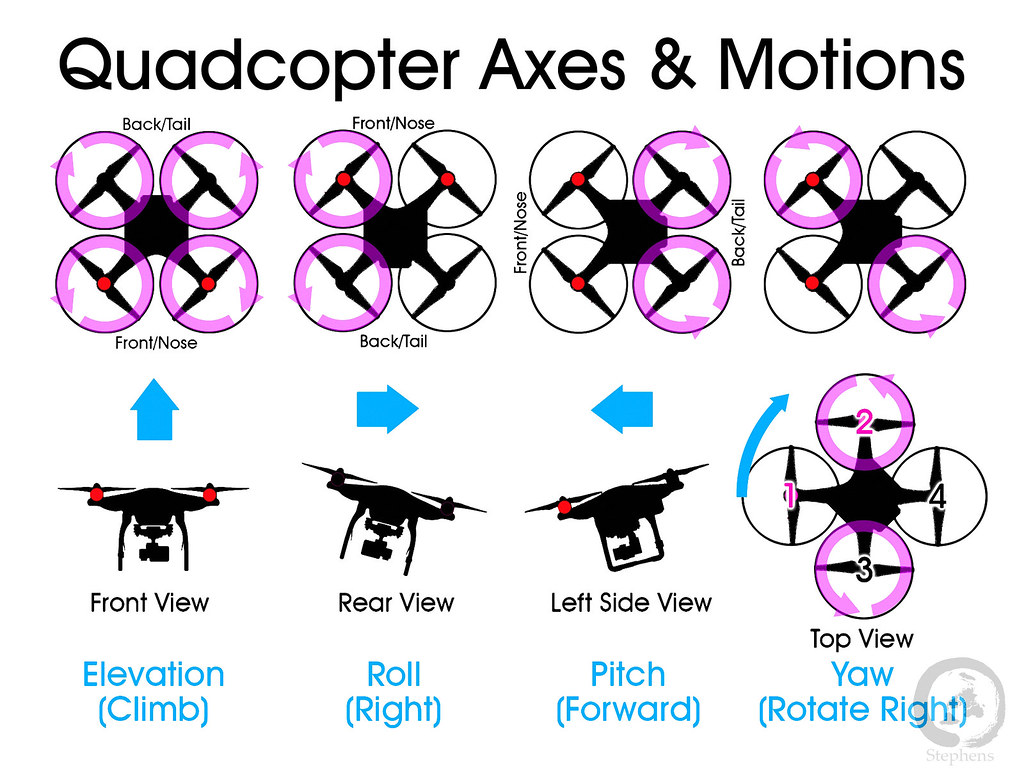
(from Link)

쿼드로터는 4개의 모터로 기동하며, 모터로 인한 추력과 기체의 무게가 동일하면 기체는 hovering 한다.

위 그림과 같이 회전 Roll, Pitch 를 통해 translation 이 가능하다. 마주보는 모터끼리 같은 방향으로 회전하는데, 한 쪽의 추력을 상대적으로 높이면서 전체 추력을 유지하면 기체는 반대 쪽으로 이동한다.

Yaw 의 경우는 시계/반시계 방향의 모터들만 회전 수를 높히면 반작용에 의해 반대 방향으로 회전한다.

Key Components of Autonomous Flight

1. State Estimation
2. Control
3. Mapping
4. Planning

자율비행을 위한 기본적인 요소들이다. 자세한 설명은 생략.

State Estimation

State estimation 은 현재 시스템의 정보를 추정하는 것이다. 드론에서는 위치 position 과 yaw 가 필요하다.

Motion capture camera 혹은 GPS 를 사용할 수도 있다.

그러나, 어느 환경에서나 state estimation 이 가능하려면 기체에 장착되며 GPS 대신 실내에도 사용가능한 센서가 필요하다.

주로 카메라, LiDAR 등이 사용된다.

이 때, 센서 정보로 인식된 외부 물체의 정보를 이용해 역으로 기체의 위치를 추정한다. 반대로 외부 물체의 정보는 기체 위치(=센서 위치)를 기반으로 추정된다.

이는 서로 간의 오차가 얽혀 있고, 이를 해결하는 것 또한 SLAM(Simultaneous Localization and Mapping) 의 문제가 된다.

최근 드론 연구분야에서는 보통 IMU, LiDAR 을 사용하고, 카메라만을 사용하는 vision-based 는 별도의 연구 분야로 보인다.(혹은 depth까지 추가한)

Energetics and System Design

Basic Mechanics

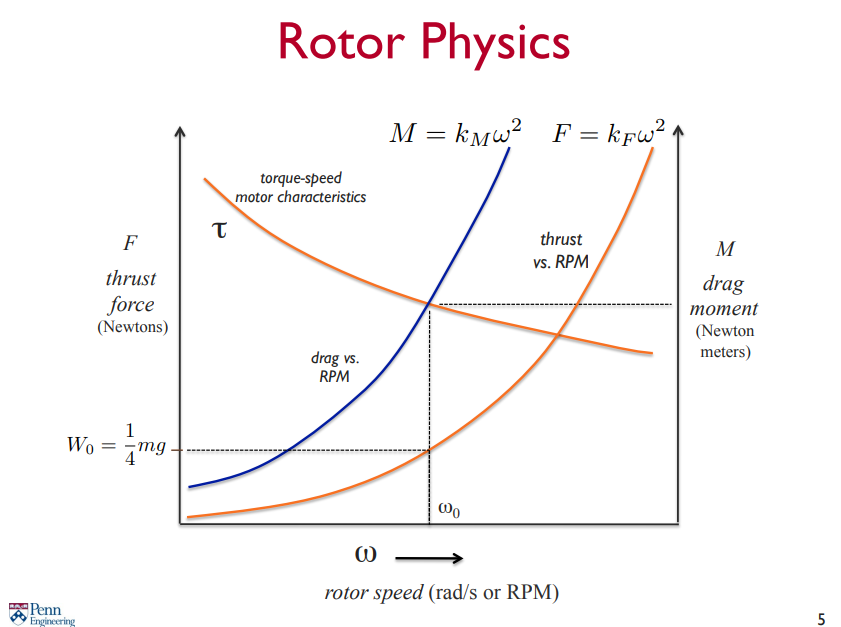
각 모터에서 내는 thrust 의 총 합으로 기체를 비행시킨다.

이 때 각 thrust 는 대략적으로 RPM 의 quadratic 하게 비례한다.

$$F=k_F{w}^2$$

이 때 회전에 의해 drag force 도 발생한다. 이 또한 quadratic 하게 비례한다.

$$M=k_M{w}^2$$

각 모터가 균등하게 무게를 나눠서 지탱해야 한다고 하면, $F=W_0=\frac{1}{4}mg$ 가 되므로 이 때의 $w_0$ 을 구할 수 있다.

하지만 이 $w_0$ 에 해당하는 $M$ 도 발생하므로, 이를 상쇄할 수 있는 모터가 필요하다.

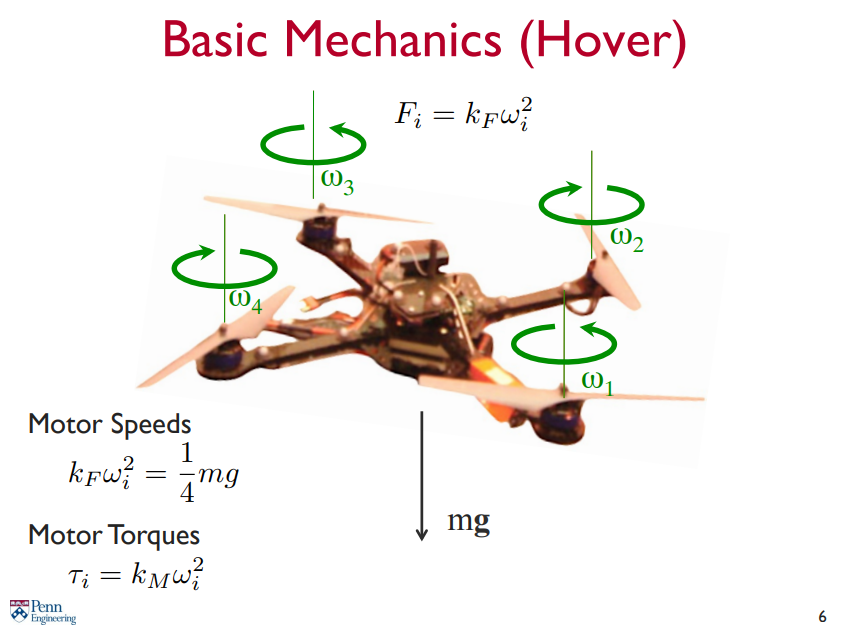
이를 정리해보면 기초적인 dynamics 를 유도할 수 있다.

hovering 하고 roll = pitch = 0 이라고 할 때, 아래와 같이 수식이 정리된다.

$$\begin{array}{r}F=\sum F_i-mg{a}_3\\ M=\sum r_i\times F_i+\sum M_i\end{array}$$

따라서 평형 상태가 깨지면 수직 방향의 가속도를 얻을 수 있다.

$$\begin{array}{r}\sum F_i-mg=ma\\ \sum k_F{w}_i^2-mg=ma\end{array}$$

Dynamics and 1-D Linear Control

이제 기초적인 제어를 살펴본다.

$$a=\frac{d^{2}x}{d{t}^2}=\ddot{x}$$

이므로 이전의 수식을 활용하여 Input $u$ 를 얻을 수 있다.

$$u=\frac{1}{m}[\sum k_F{w}_i^2+mg]$$

그렇다면 아래와 같이 문제를 정의하고 필요한 제어 입력을 수식화할 수 있다.

Probelm

• State, input $x,u\in \mathbb{R}$
• Plant model $\ddot{x}=u$
• the desired trajectory $x^{des}(t)$

General Approach

• Define error $e(t)=x^{des}(t)-x(t)$
• Make $e(t)$ to converge exponentially to zero

Strategy Find $u$ such that

$$u(t)={\ddot{x}}^{des}(t)+K_v\dot{e}(t)+K_{p}e(t)$$

일반적인 PD 제어로 볼 수 있으며, ${\ddot{x}}^{des}(t)$ 는 feedfoward term 이다.

이후에는 PD/PID 제어에서 Gain 의 영향과 tuning 에 대한 설명이므로 생략.

Design Considerations

하지만 모터에서 낼 수 있는 추력에는 한계가 있다.

전체 모터의 추력의 최댓값을 $T_{max}$ 라고 할 때, Input $u$ 의 최댓값을 표현할 수 있다.

$$u_{max}=\frac{1}{m}[T_{max}+mg]$$

PD 제어에서도 마찬가지로 제한조건이 생긴다

$$u(t)=\min ({\ddot{x}}^{des}(t)+K_v\dot{e}(t)+K_{p}e(t),u_{max})$$

따라서 가속도에 비례한 Thrust-weight ratio 가 중요해진다.

이 외에도 Power consumption 을 고려해야 한다. 그에 따라 자연스럽게 배터리와 모터의 선택이 중요해진다.

쿼드로터는 상당히 비효율적인 기체이고(인간에 비교해서), 배터리와 모터들의 무게가 전체 무게의 대부분을 차지하기 때문에 적절한 기체 설계가 중요하다.

본 강의에서는 기체의 무게를 가볍게 함으로써 이러한 비효율성을 최소화하려고 했다고 한다.

Agility and Maneuverability

Agility 민첩성을 최대화한다는 것은 정지하는데 걸리는 거리를 최소화하는 것이다.

또한 쿼드로터는 translation과 rotation이 coupled되어 있으므로 회전반경을 최소화하는 것으로 볼 수도 있다.

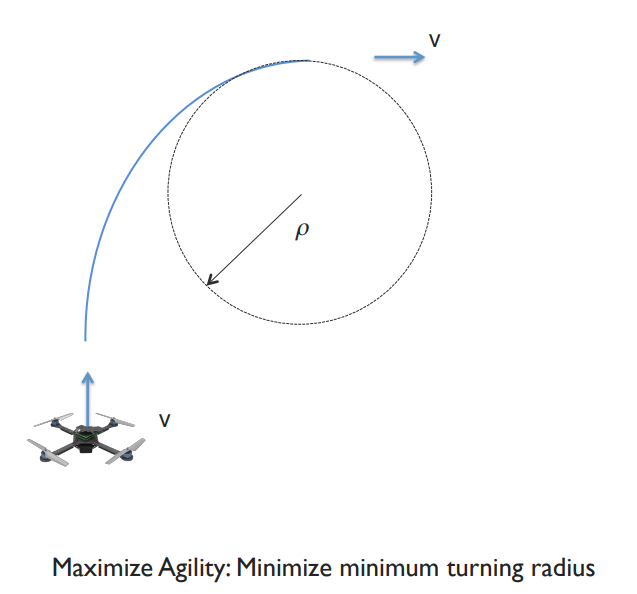
쿼드로터를 2D 평면에서만 생각해보자.

비행 중인 기체가 정지하기 위해서는 기울어진 Roll/Pitch 의 반대방향으로 힘을 가해주어야 한다.

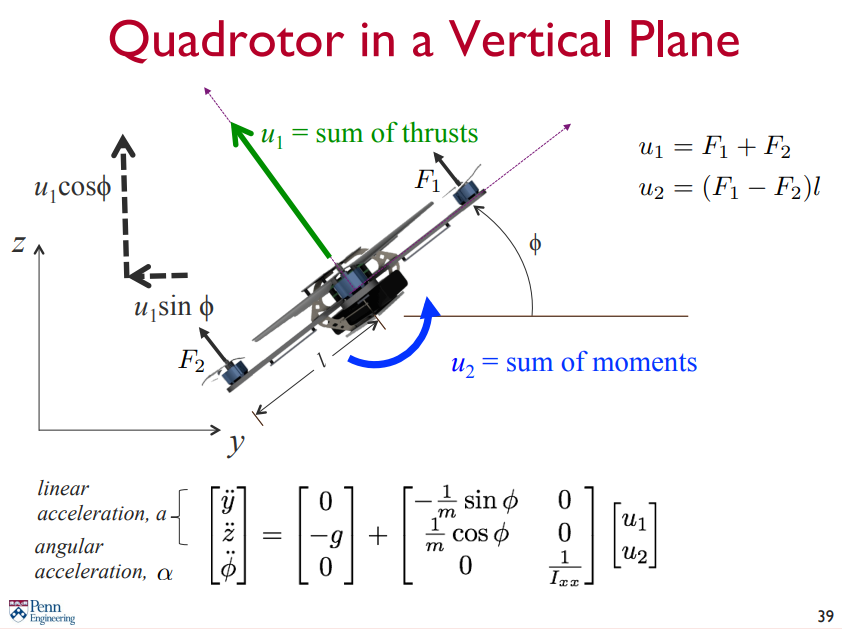
y-z 평면에서 $\varphi$ 크기의 각으로 기울어진 경우 $T=F_1+F_2,M=(F_1-F_2)l$라고 하자.

이를 각 방향으로 분해할 수 있으므로 선가속도와 각가속도를 표현할 수 있다.

$$\left[\begin{array}{c}\ddot{y}\\ \ddot{z}\\ \ddot{\varphi }\end{array}\right]=\left[\begin{array}{c}0\\ -g\\ 0\end{array}\right]+\left[\begin{array}{cc}-\frac{1}{m}sin\varphi & 0\\ \frac{1}{m}cos\varphi & 0\\ 0& \frac{1}{I_{xx}}\end{array}\right]\left[\begin{array}{c}T\\ M\end{array}\right]$$

그렇다면 Agility 를 빠르게 가속하고, roll/pitch 를 빠르게 한다고 본다면, $a_{max}=\frac{T_{max}}{W}$ 와 ${\alpha }_{max}=\frac{M_{max}}{I_{xx}}$ 를 최대화 하는 것으로 볼 수 있다.

Component Selection

기초적인 내용이므로 생략.

FC(Flight Controller) 외에도 SBC(ex. Intel Nuc i7) 과 센서들이 탑재되는데, 센서들의 성능이 좋을 수록 멀리 있는 장애물들을 인식할 수 있는 대신 무게가 높아진다.

따라서 thrust-weight-ratio가 낮아지면, 장애물을 효과적으로 회피할 수도 있지만 빠른 기동이 어려워질 수 있다.

또한 무게가 늘어나면 가능한 최대 비행시간도 줄어드므로 고려할 사항이 많아진다.

아쉬운 점은 배터리, 모터 성능과 무게에 따른 비행시간도 계산하는 내용을 다루지 않을까 하였는데 없음.

Effects of Size

Agility with Scaling

• Mass, Intertia

  $$m\sim l^3,I\sim l^5$$

  질량 $m$ 은 $\rho V$ 이고, $V\sim l^3$ 이므로 $m\sim l^3$ 이다.

  distributed mass 에 대해 관성 $I$ 는 ${\int }_V\rho r^{2}dV$ 이다. $dV\sim l^3$ 이고 $r^2\sim l^2$ 이므로 $I\sim \rho l^3\times l^2$ 이다.

• Thrust

  $$F\sim \pi r^2\times (wr{)}^2\sim l^2{v}^2$$

• Moment

  $$M\sim Fl$$

따라서, $a,\alpha$ 는 아래와 같이 근사화할 수 있다.

$$\begin{array}{r}a\sim \frac{F}{m}\sim \frac{v^2}{l}\\ \alpha \sim \frac{M}{I}\sim \frac{v^2}{l^2}\end{array}$$

그리고 $v$ 와 $l$ 의 관계를 두 가지 종류로 근사화할 수 있다.

1. Froude scaling

   $$v\sim \sqrt{l}$$

   유체역학에서 constant Froude number $Fr$ 를 위해 $Fr=\frac{v}{\sqrt{gl}}$ 을 만족해야 한다고 한다.

   그러므로, $a\sim 1,\alpha \sim \frac{1}{l}$ 가 된다.

2. Mach scaling 마찬가지로 constant Mach number $Ma$ 는 $Ma=\frac{v}{c}$ 를 만족하여 아래와 같은 관계를 가진다.

   $$v\sim 1$$

   이 경우, $a\sim \frac{1}{l},\alpha \sim \frac{1}{l^2}$ 이다.

따라서 작은 기체일 수록(smaller $l$), 최대 각가속도 ${\alpha }_{max}$ 가 커지는 것을 알 수 있다.