Geometry and Mechanics
이전 Post: Introduction
2.1 Quadrotor Kinematics
Transformations
이번 강의에서는 “Rigid Body Transformations 의 주제를 다루고, 이를 위한 notation들의 정의를 한다.
주로 사용하는 transformation matrix인 은 다음과 같이 어떤 frame에서 frame으로 바뀌는지 표현한다.
이러한 표현방식 모두 frame 에서 로 transform 한다는 의미이다.
이제 Rigid Body Displacement 를 어떤 물체 라고 할 때 Map 라고 하자.
그렇다면 안의 모든 점들은 로 transformation 을 표현할 수 있다. ex)
vector 의 이동은 로 표현한다. 그러면 와 같이 vector 간의 transformation 도 표현된다.
벡터의 크기와 cross-product 는 그대로 유지된다.
마찬가지로 orthogonal vector 끼리도 유지되어야 unit vectors(or xyz axes) 가 보존된다.
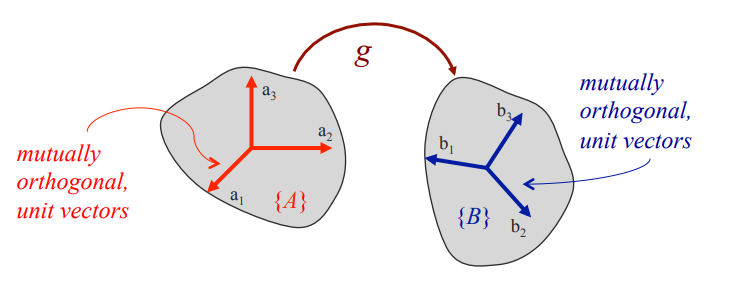
위와 같은 Rigid body 의 unit vector transformation을 아래와 같이 linear combination으로 표현할 수 있다.
각 계수들의 notation은 맨 처음 정의한 notation을 참고해서 생각해보자. (matrix의 column, row로 볼 수도 있지만)
그러면 아래와 같이 Rotation matrix 을 정의할 수 있다.
Note
- Rotation about the x-axis through
- Rotation about the y-axis through
- Rotation about the z-axis through
Rotations
이러한 Rotation matrix 은 orthogonality 와 determinant가 1인 special orthogonality를 가진다.
이는 Special Orthogonal group인 에 속한다.
이를 표현하는 방법으로는 아래와 같다.
- Rotation matrices
- Euler angles
- Axis angle parameterization
- Exponential coordinates
- Quaternions
이 중, 어떤 방식이 coordinates for 가 될 수 있는지 알아보자.
Euler Angles
Euler angles은 어떤 에서 로의 회전을 3가지의 회전의 조합으로 나타내는 것이다.
어떤 회전이든 이러한 연속적인 3가지의 회전을 linearly independent 한 axes 의 조합으로 볼 수 있다.
하지만 rotation matrix 3 Euler angles 는 성립하지 않고 almost one-to-one 이다.
그러한 이유를 살펴보자.
Euler angles는 어떤 순서로 axes 를 조합하느냐에 따라 다르게 표현할 수 있다. 앞선 수식에서는 X-Y-Z Euler angles 라고 할 수 있다.(Roll-Pitch-Yaw 순)
Gimbal Lock 상황을 위해 Z-Y-Z Euler angles 를 예시로 들어보자.
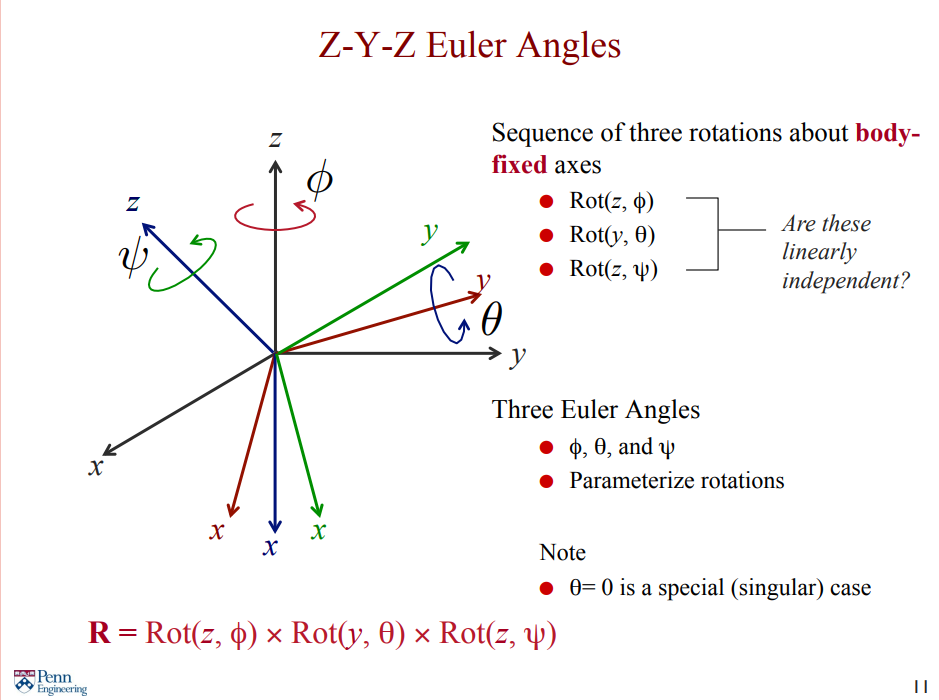
Body-fixed frame 에서 z축에 대해 만큼, y축에 대해 만큼, z축에 대해 만큼 회전시킨다.
Body-fixed frame 에서 회전하므로 회전이 이루어질 때마다 기존의 축이 바뀌기 때문에 새로운 y 혹은 z축에 대해 회전하고 있다.
이들의 회전은 모두 linearly independent 한 것을 알 수 있다. 하지만 인 경우에는 더이상 linearly independent하지 않기 때문에, unique 하게 표현할 수 없다.
이를 Rotation matrix로 살펴보자.
여기에서 만약 를 알고 있다면, 를 계산할 수 있고 를 통해 를, 을 통해 를 알 수 있다.
하지만 만약 이라면 이고, 나머지 항들이 와 의 조합으로 이루어져 있으므로 해가 무한해진다.
이를 요약하면 아래 슬라이드와 같다.

Axis/Angle Representations for Rotations
Euler는 아래와 같이 회전을 정의하였다.
Euler's Therorem
Rotations Any displacement of a rigid body such that a point on the rigid body, say , remains fixed, is equivalent to a rotation about a fixed axis through the point .
앞서 Rotation matrix 나 Euler angle 에서는 회전축에 대한 이야기가 없었으나, Euler 는 위와 같이 회전을 정의하였다.
어떤 회전을 아래 사진과 같이 원점을 같게 만들어 표현해보자.
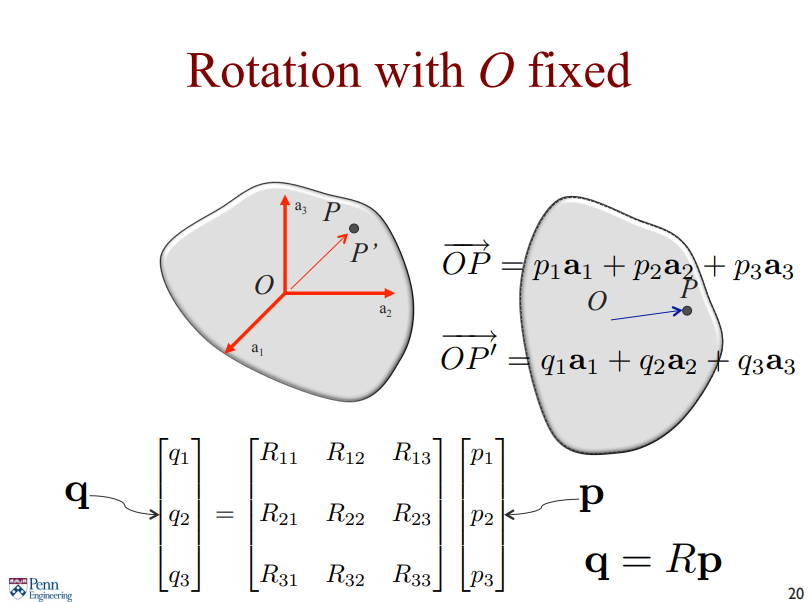
그러면 회전한 를 회전하기 전과 같은 원점을 갖는 (blue arrow) 로 표현할 수 있고, 이는 같은 unit vector 를 공유한다.
따라서, 이들의 계수는 새로운 linear combination 이고 Rotation matrix 을 정의할 수 있다.
그렇다면 Euler’s Theorem 을 증명해보자.
에서 자기자신에게 대응되는 가 있을까? 그렇다면 가 되고, 그렇다는 것은 eigenvalue 가 1인 을 의미한다.
바꿔 말하면, 의 eigenvalue 문제의 해가 1이라는 것을 의미한다.
이제는 주어진 임의의 회전축 와 회전각 가 있다고 해보자. 이를 이용해 Rotation matrix 을 유도해보자. (회전축 가 좌표축 중 하나라면 앞선 Euler angles 와 동일하다.)
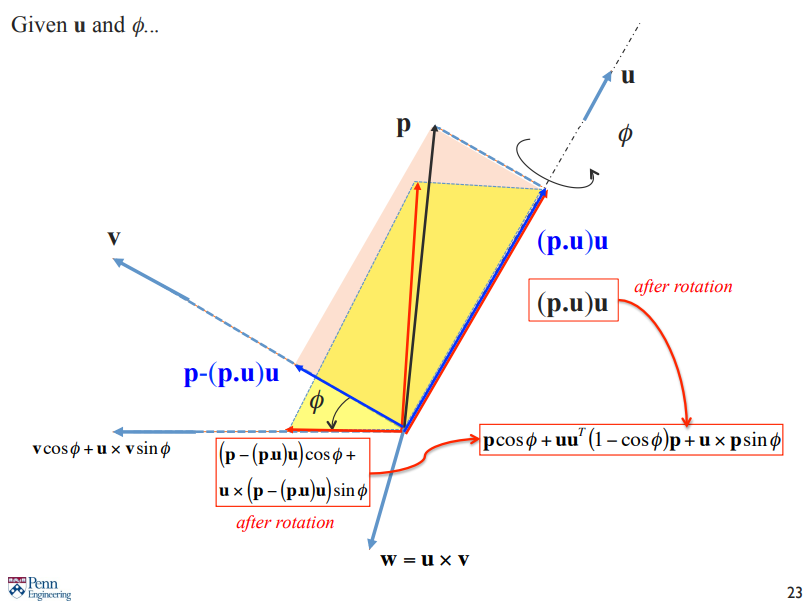
그래서 위 사진과 같이 벡터 를 회전축과 평행한 요소와 수직인 요소로 분해한다. 그러면 평행한 요소 는 회전과 상관없이 변하지 않는다.
각도 만큼 회전하면 수직한 요소인 는 아래와 같이 표현된다.
풀어 설명하면 에 수직한 요소를 라고 하였을 때, 이를 외적한 를 만들 수 있고 이들의 이다.
그렇다면 회전하고 난 은 가 된다.
자기 자신의 외적은 0임을 이용해 으로 위 수식을 정리하면,
와 같다.
이제 외적 부분을 행렬 로 표현한다. 이는 skew-symmetric matrix 로, 를 만족하고 이들의 diagonal element 들은 모두 0이다. ()
이제 를 제거하면 임의의 벡터에 대해 회전축 와 회전각 를 갖는 수식을 얻을 수 있고, 이것이 Rodrigues’ formula 이다.
그렇다면 이러한 방식이 Rotation matrix 에 onto or one-to-one 대응일까?
앞서 Euler’s Theorem에서 onto 임은 살펴보았다.
그러나, 와 의 예시를 통해 one-to-one 은 아닌 것을 알 수 있다.
Rotation matrix 로 부터 회전축 와 회전각 를 얻어보자.
이라고 하면 가 된다. 그리고 로 를 얻을 수 있다.
이 때 인 경우에는 이 되어 unique 한 회전축 를 얻을 수 없다. 또한, 인 경우 가 되어 를 얻게 됨을 알 수 있다.
따라서, 정의역을 로 하더라도 일대일 대응이 될 수 없다.
Angular Velocity
회전 속도는 회전의 변화율로, 회전의 시간에 대한 미분이다.
Rotation matrix 에 대해 orthogonality 를 만족해야 하므로, 로 부터 아래와 같은 식을 유도할 수 있다.
이를 통해 은 skew-symmetric matrix 임을 알 수 있다. ()

이전에 보았던 예시에서 이제는 가 되어 는 여전히 시간에 변화와 관계없이 고정임을 알 수 있다.
이에 대한 미분은 이다. 이 때 는 body-fixed frame 에서의 위치이지만, 는 inertial frame 에서의 속도이다.
양변에 를 곱해보자. 그러면 가 되고, 좌항은 속도를 다시 body-fixed frame 으로 transformation 시켰고 우항은 body-fixed frame 에서의 각속도가 된다. 이 때 이 skew-symmetrix matrix 이므로 로 표현한다.
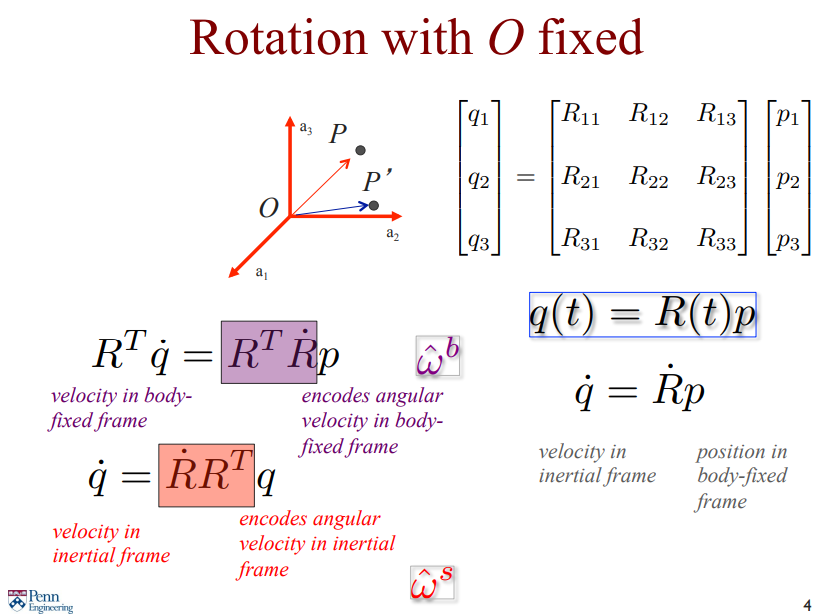
그리고 의 양변에 를 곱하면 를 얻을 수 있다.
이렇게 되면 좌항은 inertial frame 에서의 속도이고, 우항은 inertial frame 에서의 각속도가 된다. 마찬가지로 를 로 표시한다.
2.2 Quadrotor Dynamics
Dynamics of a Quadrotor
이제 쿼드로터의 Dynamics 를 알아보자.
이전 강의에서 다룬대로 로 힘과 모멘트가 정의된다.
그리고 Z-X-Y Euler angles convention 을 사용한다.
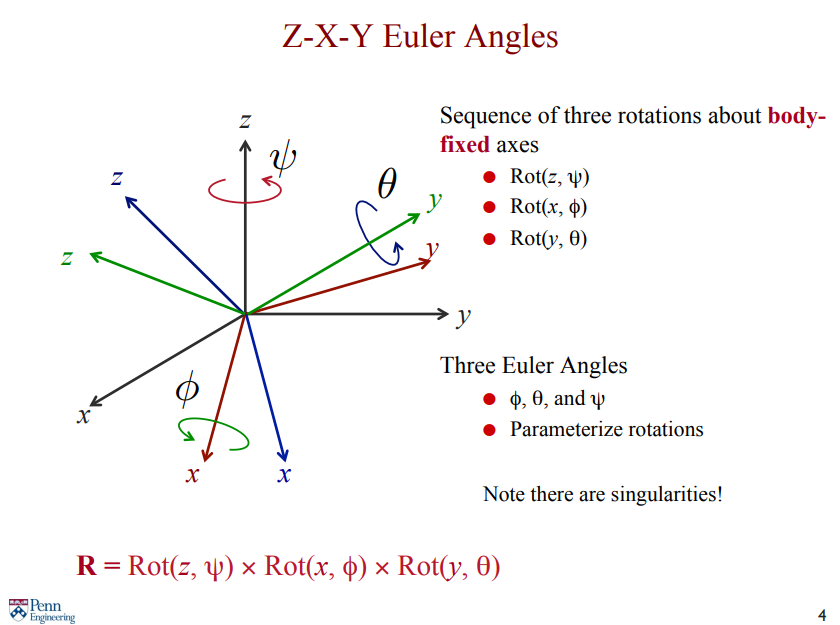
이에 따라 아래와 같은 Dynamics 표현이 가능하다.
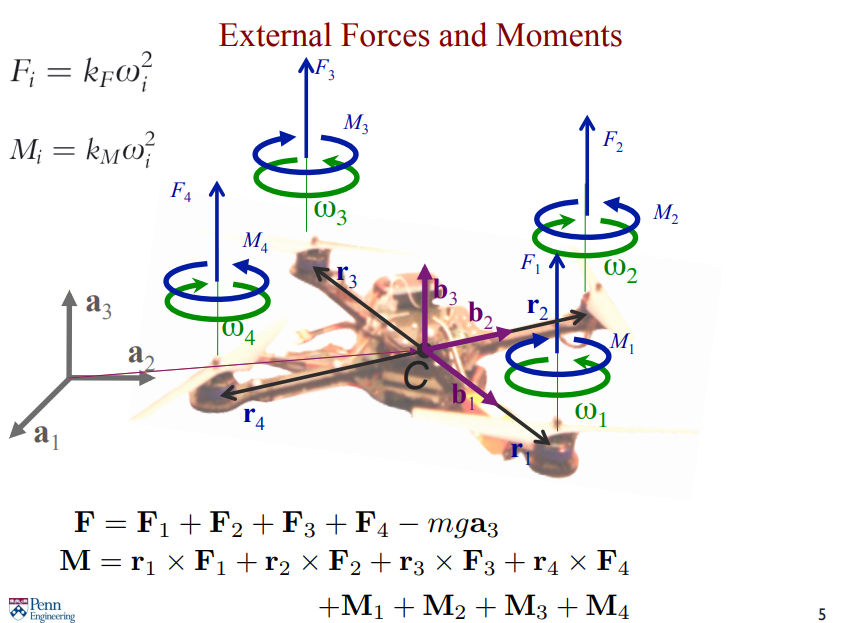
Newton-Euler Equations
기체의 COM 을 로 구할 수 있고, 로 표현한다.
Momentum 의 미분인 Angular momentum 은 로 표현할 수 있다. 는 inertia tensor 로, 기준점에 관계없이 절대적이다.
Principal Axes and Principal Moments of Inertia
Principle axis of inertia is a unit vector along a principal axis if is parallel to . There are 3 independent principal axes.
Principal moment of inertia The moment of inertia with respect to a principal axis, is called a principal moment of inertia.

앞선 주축과 주모멘트 정의에 의해 inertial frame 와 body-fixed frame , origin 에 대해서 위와 같이 표현해볼 수 있다.
frame 에서의 주축을 좌표축으로 잡아 각속도 를 로 표현할 수 있다.
의 좌항을 분해하여 로 표현하여 움직이는 물체를 inertial frame 의 모멘텀을 표현할 수 있다.
앞서 주축으로 unit vector 를 구성하였으므로, 이므로 로 정리된다.
이를 모두 정리한 것이 그림의 보라색 박스 이다.
Quadrotor Equations of Motion
이를 정리하여 아래의 수식으로부터 Equations of Motion 만들어보자.
이를 앞선 설명들로 모두 표현하면
가 된다. ( = position in inertial frame, = length of the airframe)
여기에서 은 모두 기체의 길이, 질량, 관성이므로 쉽게 구할 수 있다.
그리고 앞선 Z-X-Y Euler angles 를 통해 Roll, Pitch, Yaw 로 부터 각속도를 구할 수 있다.
따라서 3차원에 State Space 를 구성할 수 있다.
State Space of Quadrotors
