[Aerial Robotics] Planning and Control

3.1 Control

2-D Quadrotor Control

앞서 Dynamics 에 대해서는 많이 살펴보았다. 1-D Quadrotor Control 에서 처럼 system modeling 을 통한 간단한 PD 제어기를 만들어보자.

2-D Control 에서는 y-z plane 에서의 움직임만 고려한다.

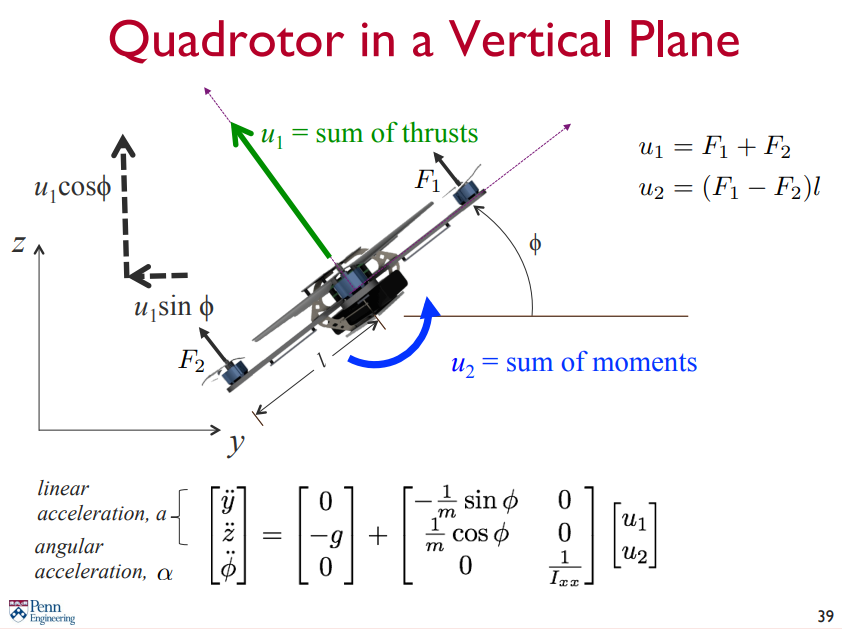
이전에 Equations of motion 을 살펴보았다.

이제 Trajectory tracking 을 수행해보자. 주어진 desired trajectory $r_T(t)=\left[\begin{array}{c}y(t)\\ z(t)\end{array}\right]$ 에 대해 PD 제어를 수행하기 위해서는 제어기 구조가 아래와 같이 되어야 한다.

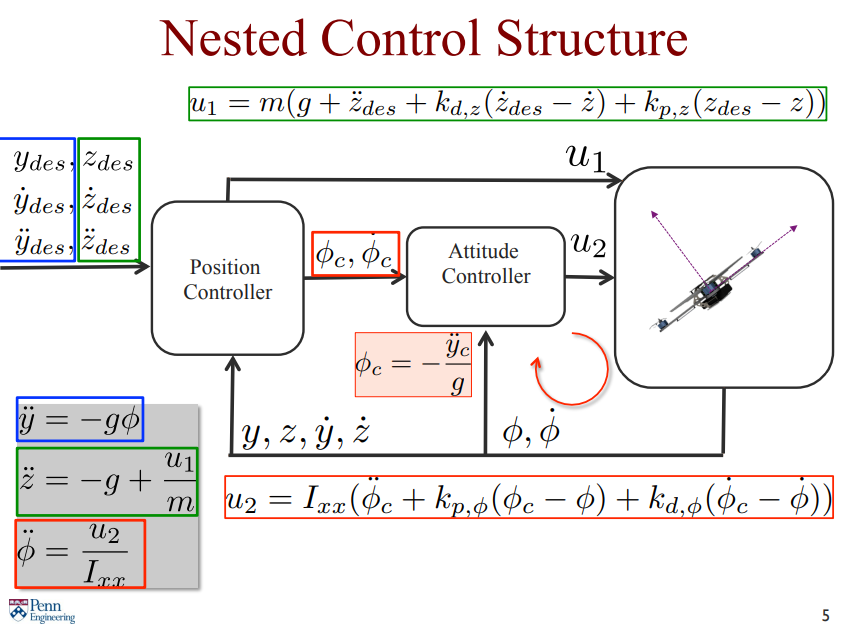
$\ddot{z}=-g+\frac{u_1}{m}$ 이므로 $u_1=m(g+\ddot{z})$ 가 된다. 여기에 Feedback 기반 PD 제어를 하므로 초록색 박스 와 같아진다.

그러므로 위치 제어기에서 $u_1$ 이 구해지고 ${\varphi }_{command}=-\frac{{\ddot{y}}_c}{g}$ 를 $u_2$ 를 구하는데 사용한다.

$u_2$ 에 있는 ${\ddot{\varphi }}_c$ 는 $-y^{(4)}/g$ 이므로 snap 에 비례한다. tracking 해야하는 궤적이 aggressive 하지 않다면 $snap\approx 0$ 으로 여긴다. 또한, $I_{xx}$ 또한 생략하여 최종적인 $u_2$ 는 아래와 같다.

$$u_2=k_{p,\varphi }({\varphi }_c-\varphi )+k_{d,\varphi }({\dot{\varphi }}_c-\dot{\varphi })$$

이제 기체의 state 에서 나온 current state $x$ 가 feedback 되어 2-D PD 제어를 수행할 수 있다.

3-D Quadrotor Control

이제 이를 확장하여 3D Control 을 수행해보자. 앞선 1D, 2D 와 달리 yaw 또한 고려된다.

그러므로 desired trajectory $r_T(t)=\left[\begin{array}{c}x(t)\\ y(t)\\ z(t)\\ \psi (t)\end{array}\right]$ 가 된다.

그리고 Momentum $M$ 계산에 필요한 각속도 $\omega$ 는 앞서 배운대로 Roll, Pitch, Yaw 로 부터 구할 수 있다.

$$\left[\begin{array}{c}{\omega }_x\\ {\omega }_y\\ {\omega }_z\end{array}\right]=\left[\begin{array}{ccc}c\theta & 0& -c\varphi s\theta \\ 0& 1& s\varphi \\ s\theta & 0& c\varphi c\theta \end{array}\right]\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]$$

이제 우리의 state $x=\left[\begin{array}{c}q\\ \dot{q}\end{array}\right],\text{s.t}q=\left[\begin{array}{c}x\\ y\\ z\\ \varphi \\ \theta \\ \psi \end{array}\right]$ 가 된다. ($\varphi ,\theta ,\psi$ = Roll, Pitch, Yaw)

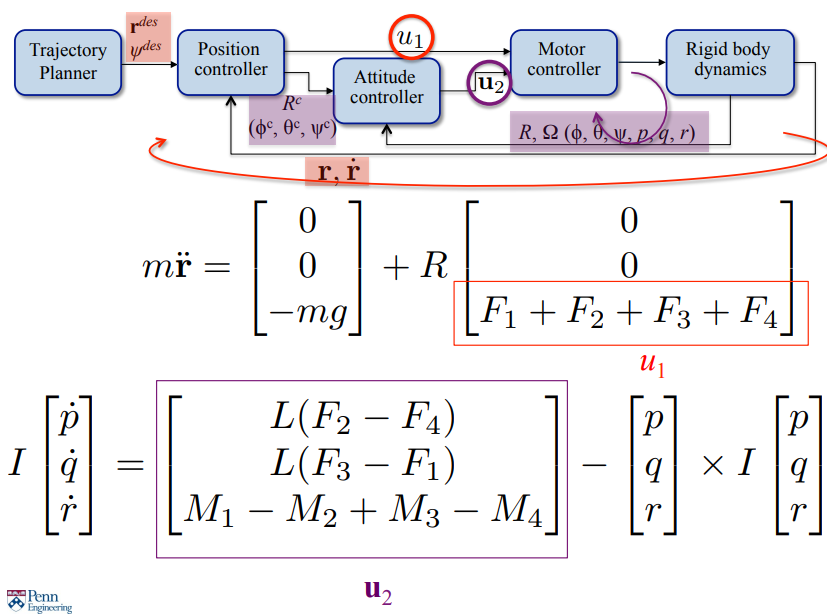
제어기 구조는 위와 같다. Outer loop 는 이전에 알던대로 위치 제어기의 feedback loop 이다.

Inner loop 에서는 ${\varphi }_c,{\theta }_c,{\psi }_c$ 를 자세제어기에 넣어준 후, Dynamics 를 이용해 current state 를 얻어 $u_2$ 의 feedback loop 가 완성된다.

Control for Hovering

3D Hovering 의 경우에는 $u_1\sim mg,\theta \sim 0,\varphi \sim 0,\psi \sim {\psi }_0$ 와 $u_2\sim 0,{\omega }_x\sim 0,{\omega }_y\sim 0,{\omega }_z\sim 0$ 으로 가정한다.

Linear Momentum Equation Near Hover

우선 linear momentum equation 부터 살펴보자. Z-X-Y Euler angles 를 이용하면 $R$ 을 이용해 아래와 같이 표현된다.

$$\begin{array}{rl}m\ddot{x}& =(\cos \psi \sin \theta +\cos \theta \sin \varphi \sin \psi )u_1\\ m\ddot{y}& =(\sin \psi \sin \theta -\cos \psi \cos \theta \sin \varphi )u_1\\ m\ddot{z}& =-mg+(\cos \varphi \cos \theta )u_1\end{array}$$

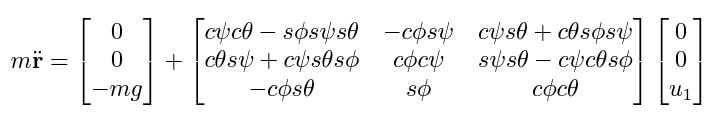
이 때 근사를 이용해 $\sin \theta \approx \theta ,\cos \theta \approx 1$ 를 넣어보면 아래와 같이 정리된다. ($\varphi \sim {\varphi }_0$ 이므로 Yaw 는 근사하지 않는다.)

$$\begin{array}{rl}m\ddot{x}& =(\theta \cos \psi +\varphi \sin \psi )u_1\\ m\ddot{y}& =(\theta \sin \psi -\varphi \cos \psi )u_1\\ m\ddot{z}& =-mg+u_1\end{array}$$

Angular Rates Near Hover

마찬가지로 angular rates 로 한다.

$$\begin{array}{rl}p& =\dot{\varphi }\cos \theta -\dot{\psi }\cos \varphi \sin \theta \\ q& =\dot{\theta }+\dot{\psi }\sin \varphi \\ r& =\dot{\varphi }\sin \theta +\dot{\psi }\cos \varphi \cos \theta \end{array}$$

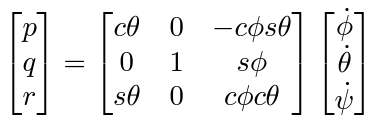
또 똑같이 근사한다.

$$\begin{array}{rl}p& =\dot{\varphi }-\dot{\psi }\theta \\ q& =\dot{\theta }+\dot{\psi }\varphi \\ r& =\dot{\varphi }\theta +\dot{\psi }\end{array}$$

여기서 0과 가까운 값의 곱은 0으로 근사할 수 있다. 즉, $\dot{\psi }\theta \approx \dot{\psi }\varphi \approx \dot{\varphi }\theta \approx 0$ 이다.

결국 $p=\dot{\varphi },q=\dot{\theta },r=\dot{\psi }$ 가 된다.

Angular Momentum Equation Near Hover

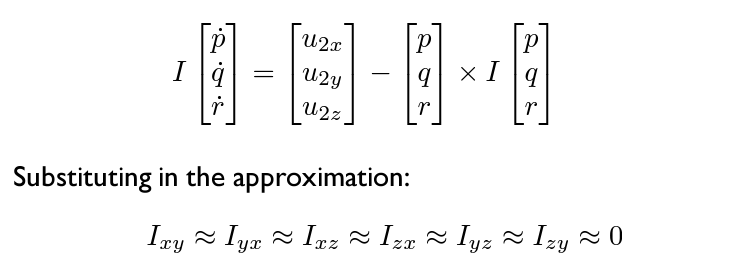
식을 정리하면 아래와 같다.

$$\begin{array}{rl}\left[\begin{array}{ccc}{I}_{xx}& 0& 0\\ 0& I_{yy}& 0\\ 0& 0& I_{zz}\end{array}\right]\left[\begin{array}{c}\dot{p}\\ \dot{q}\\ \dot{r}\end{array}\right]& =\left[\begin{array}{c}{u}_{2x}\\ u_{2y}\\ u_{2z}\end{array}\right]-\left[\begin{array}{ccc}0& r& -q\\ -r& 0& p\\ q& -p& 0\end{array}\right]\left[\begin{array}{ccc}{I}_{xx}& 0& 0\\ 0& I_{yy}& 0\\ 0& 0& I_{zz}\end{array}\right]\left[\begin{array}{c}p\\ q\\ r\end{array}\right]\\ I_{xx}\dot{p}& =u_{2x}-I_{yy}qr+I_{zz}qr\\ I_{yy}\dot{q}& =u_{2y}-I_{xx}pr-I_{zz}pr\\ I_{zz}\dot{r}& =u_{2z}-I_{xx}pq+I_{yy}pq\end{array}$$

여기서 한번 더 정리가 가능한데, 이전처럼 0에 가까운 값들의 곱은 0으로 근사할 수 있다. 즉, $qr\approx pr\approx pq\approx \dot{\theta }\dot{\psi }\approx \dot{\varphi }\dot{\psi }\approx \dot{\varphi }\dot{\theta }\approx 0$ 이다.

$$\begin{array}{rl}{I}_{xx}\dot{p}& =u_{2x}\\ I_{yy}\dot{q}& =u_{2y}\\ I_{zz}\dot{r}& =u_{2z}\end{array}$$

이전에 angular rates 에서 유도된 $p=\dot{\varphi },q=\dot{\theta },r=\dot{\psi }$ 를 대입하면 아래와 같다.

$$\begin{array}{rl}\ddot{\varphi }& =\frac{u_{2x}}{I_{xx}}\\ \ddot{\theta }& =\frac{u_{2y}}{I_{yy}}\\ \ddot{\psi }& =\frac{u_{2z}}{I_{zz}}\end{array}$$

Linearization of Quadrotor Equations of Motion

3.2 Planning

Time, Motion and Trajectories

이제 Quadrotor의 궤적 생성에 대해 다뤄본다.

일반적으로 아래와 같은 구성을 가진다.

• Start, Goal positions
• Waypoint positions (intermediate positions)
• Smoothness criterion : Dynamical system 이므로 임의적인 궤적은 따라갈 수 없다. input 의 변화율을 최소화하는 것을 의미한다.
• Order of the system ($n$) : $n$ -th order system 이라는 것은 위치의 $n$차 미분을 input 으로 가진다는 것을 의미한다.

Calculus of Variations

$$x^{\ast }(t)=\arg \underset{x(t)}{\min }{\int }_0^T\mathcal{L}(\dot{x},x,t)dt$$

위 수식은 $\mathcal{L}$ 을 최소화하는 함수 $x(t)$ 를 찾고자 함을 의미한다.

예를 들어, 최단거리 문제의 경우 $x^{\ast }(t)=\arg {\min }_{x(t)}{\int }_0^T{\dot{x}}^{2}dt$ 가 되고 최소시간 문제 (Fermat’s principle (optics))의 경우 $x^{\ast }(t)=\arg {\min }_{x(t)}{\int }_0^{T}1dt$ 가 된다.

functional $\mathcal{L}$ 과 관계없이 Euler Lagrange equations 를 만족해야 한다.

Euler Lagrange Equation

$$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})-\frac{\partial L}{\partial x}=0$$

$n=1$ 인 system 을 살펴보자. 이 경우 input $u=\dot{x}$ 이므로 $x^{\ast }(t)=\arg {\min }_{x(t)}{\int }_0^T{\dot{x}}^2$ 를 구하는 문제가 된다.

$\mathcal{L}(\dot{x},x,t)={\dot{x}}^2$ 이므로 $\ddot{x}=0$ 이고 이를 풀어보면 $x=c_{1}t+c_0$ 이다. 나머지 계수들은 주어진 start, goal position 인 $x(0)=x_0,x(T)=x_T$ 를 이용하여 구한다.

이러한 문제는 보통 kinematic model 에서 사용가능한다. Quadrotor 와 같은 dynamics system 은 $n$ 차 system 이므로 조금 더 복잡해진다.

$$\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{d^2}{d{t}^2}(\frac{\partial L}{\partial \ddot{x}})+\cdots +(-1{)}^n\frac{d^n}{d{t}^n}(\frac{\partial L}{\partial x^{(n)}})=0$$

추후에 다루겠지만 quadrotor 는 $n=4$ 인 snap 을 input 으로 사용한다.

Minimum Jerk Trajectory

이전과 마찬가지로 $n=3$ 에 대해 궤적을 만들면 위와 같이 6개의 계수를 갖는 polynomial 궤적이 만들어진다.

이에 대해 Boundary conditions 를 적용해 $x(0)=x_0,x(T)=x_T$ 로 계수를 구한다. 이 때, $n-1$ 차 까지의 미분인 속도와 가속도는 0을 갖는다고 가정한다.

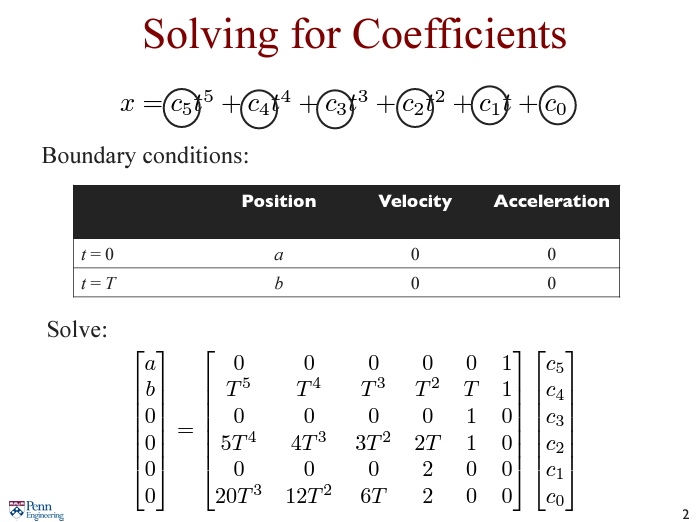
그러면 위와 같이 행렬로 구해낼 수 있다.

Extensions to multiple dimensions

이를 여러 차원으로 확장할 수 있다.

$$(x^{\ast }(t),y^{\ast }(t))=\arg \underset{x(t),y(t)}{\min }{\int }_0^T\mathcal{L}(\dot{x},\dot{y},x,y,t)dt$$ $$\begin{array}{r}\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})-\frac{\partial L}{\partial x}=0\\ \frac{d}{dt}(\frac{\partial L}{\partial \dot{y}})-\frac{\partial L}{\partial y}=0\end{array}$$

따라서 Quadrotor 의 planar motions 에 적용해보면 $(x,y,\theta )$ 에 대해 사용하므로 아래와 같이 minimum-jerk trajectory 를 구할 수 있다.

$$\underset{x(t),y(t),\theta (t)}{\min }{\int }_0^1(\text{dddot}{x}^2,\text{dddot}{y}^2,\text{dddot}{\theta }^2)dt$$

Waypoint Navigation

실제 환경에서는 중간 경로점들을 지나도록 해야한다. 즉, multi-segment trajectories 가 필요해진다.

그리고 이러한 궤적들 간의 continuous & differentiable 을 만족해야 한다.

$$\begin{array}{rl}t& ={\left[\begin{array}{ccccc}{t}_0& t_1& t_2& \dots & t_m\end{array}\right]}^T\\ x& ={\left[\begin{array}{ccccc}{x}_0& x_1& x_2& \dots & x_m\end{array}\right]}^T\end{array}$$

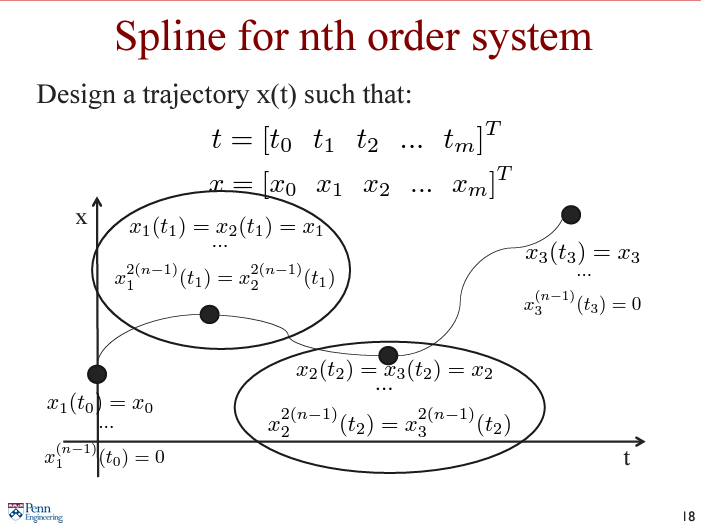
위와 같은 궤적 $\mathbf{x}(t)$ 가 정의되어야 하고, 이는 각각 아래와 같이 만족해야 한다.

$$x(t)=\{\begin{array}{l}{x}_1(t),t_0\le t<t_1\\ x_2(t),t_1\le t<t_2\\ \cdots \\ x_m(t),t_{m-1}\le t<t_m\end{array}$$

그리고 continuous & differentiable 을 위해 $t_i$ 에서 $n-1$ 차까지 각 segment 간의 값이 같아야 한다. 즉, $x_{i-1}^{[n-1]}(t_i)=x_i^{[n-1]}(t_i)$ 이어야 한다.

Motion Planning for Quadrotors

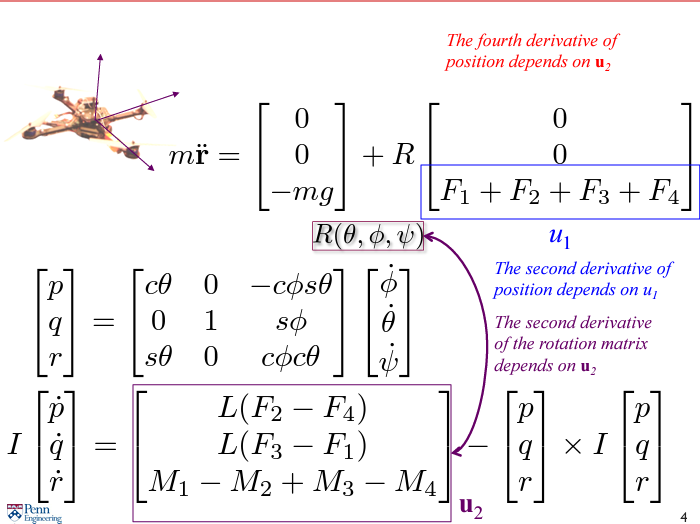
이전의 control loop 를 떠올려 보면 inner loop 에서는 attitude control 로 $u_2$ 를 결정하고 outer loop 에서 position control 로 $u_1$ 을 결정하였다.

위의 dynamics 에서 보다싶이, $u_1$ 은 position 에 대해 2차 미분 term 이다(acceleration 이므로). $u_2$ 는 rotation matrix $R$ 의 2차 미분 term 인데 이는 position 에 대해서는 4차 미분으로 얽혀 있음을 알 수 있다.

Linearization of Equations of Motion 참고

그러므로 quadrotor 에서는 Minimum snap trajectory 를 필요로 함을 알 수 있다.

$$x^{\ast }(t)=\arg \underset{x(t)}{\min }{\int }_0^T(x^{(iv)}{)}^{2}dt$$

또한 여기에 장애물 constraints 를 고려한다고 생각해보자.

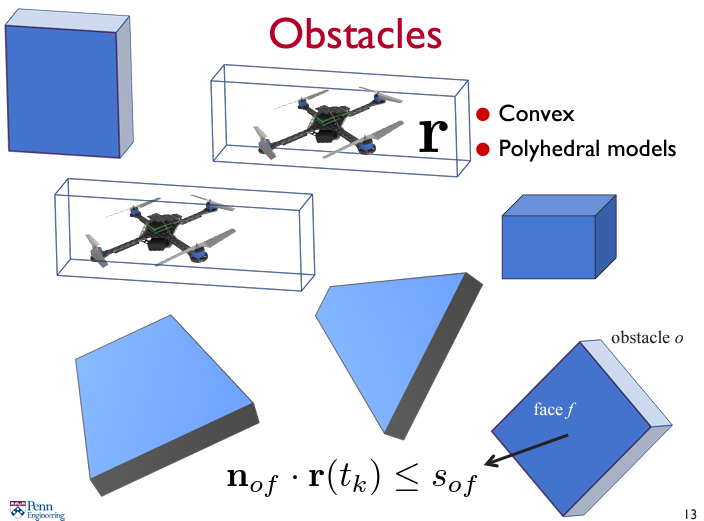
이 경우 각 장애물들을 convex 한 물체로 구성한다(e.g. Sphere, Polyhedron, etc.). 다면체의 경우 각 면의 법선 벡터와 점을 이용해 inequality constraint 를 구성할 수 있다.

강의에서는 위와 같이 장애물 constraints 를 수식화하였다.

여기에 $M{b}_{ofk}$ 항이 붙은 이유는 장애물의 모든 face 에 대해 만족할 필요가 없고 하나에 대해서만 만족해도 되기 때문이다.

$b_{ofk}$ 가 0 또는 1이기 때문에 1인 경우에는 매우 큰 $M$ 에 의해 constraints 가 항상 만족하게 된다. 그러므로 각각의 장애물에서 적어도 한 면에 대해 constraint 를 만족해야 한다.

Solving for Coefficients of Minimum Jerk Trajectories

이전에 Minimum jerk trajectory 의 계수를 찾는 문제를 조금 구체적으로 풀어보자.

이를 행렬로 표현해보면 아래와 같다.

$$\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{c}_5\\ c_4\\ c_3\\ c_2\\ c_1\\ c_0\end{array}\right]=a$$ $$\left[\begin{array}{cccccc}{T}^5& T^4& T^3& T^2& T& 1\end{array}\right]\left[\begin{array}{c}{c}_5\\ c_4\\ c_3\\ c_2\\ c_1\\ c_0\end{array}\right]=b$$

이 외에도 velocity constraints, acceleration constraints 가 있다. 즉, $0$과 $T$ 에서 미분값이 0이어야 한다.

이를 합쳐서 한번에 행렬로 표현해보면 아래와 같음을 알 수 있다.

$$\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 1\\ T^5& T^4& T^3& T^2& T& 1\\ 0& 0& 0& 0& 1& 0\\ 5T^4& 4T^3& 3T^2& 2T& 1& 0\\ 0& 0& 0& 2& 0& 0\\ 20T^3& 12T^2& 6T& 2& 0& 0\end{array}\right]\left[\begin{array}{c}{c}_5\\ c_4\\ c_3\\ c_2\\ c_1\\ c_0\end{array}\right]=\left[\begin{array}{c}a\\ b\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$

따라서 $Ax=b$ 의 문제로 바뀌어 $x=A^{-1}b$ 로 풀어낼 수 있다.