[T-Mech '24] SGS-Planner: A Skeleton-Guided Spatiotemporal Motion Planner for Flight in Constrained Space

SGS-Planner: A Skeleton-Guided Spatiotemporal Motion Planner for Flight in Constrained Space

T. Li, S. Zhang, X. Zhang, Q. Dong, and J. Huang, “SGS-Planner: A Skeleton-Guided Spatiotemporal Motion Planner for Flight in Constrained Space,” IEEE/ASME Transactions on Mechatronics, pp. 1–12, 2024, doi: 10.1109/TMECH.2024.3393144.

이 논문은 올해 T-Mech Accept 된 논문으로 기존의 SOTA 로 여겨진 GCOPTER 기반의 nonlinear optimization 방식으로 경로를 생성하던 방식 대신 hierarchical framework 기반의 QP 로 경로를 생성하였다.

따라서, 어떤 부분에서 뚜렷한 contribution 이 있었고 motion planning 에서 얻어갈 요소가 있을지 찾아보자.

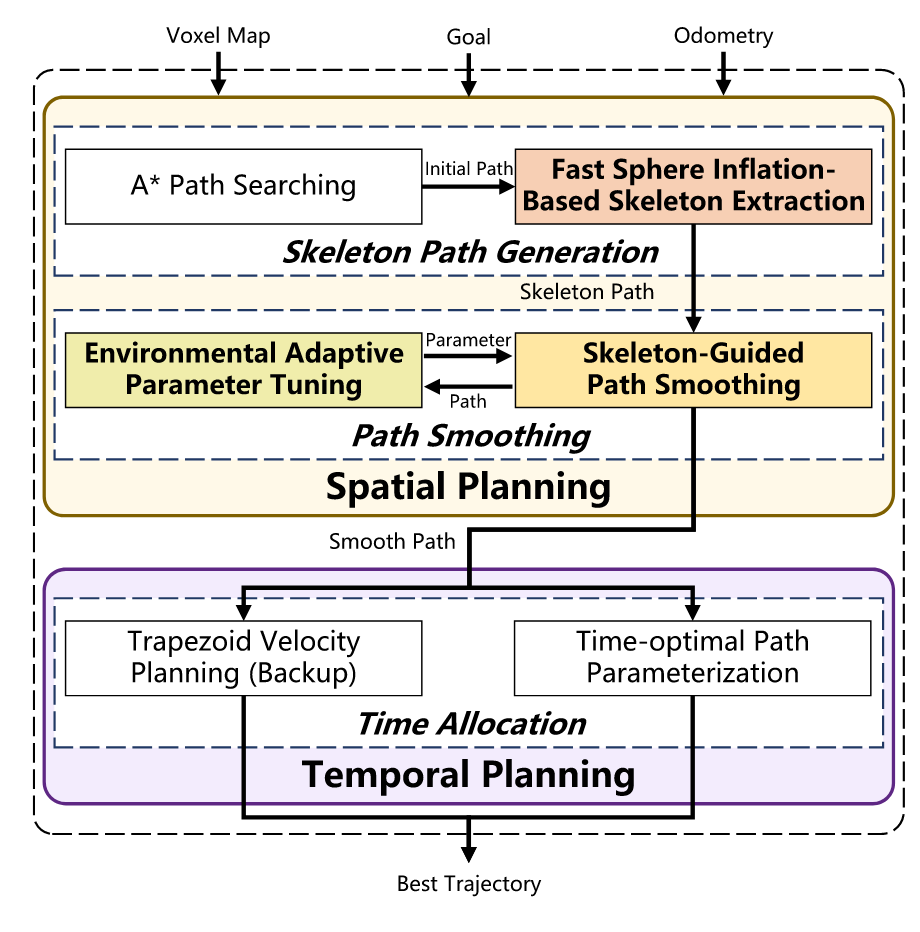
주요 contributions

1. hierarchical motion planner 로 spatial 과 temporal planning 을 순차적으로 진행한다.
2. skeleton 기반의 sphere inflation method 를 제안하여 빠르고 안전한 경로를 만들 수 있게 하였다.
3. environmental adaptive parameter tuning 을 통해 path smoothing 이 이루어진다. 이는 unconstrained QP 를 풀어 closed-form solution 도 얻어내 해결한다.

Introduction

본 논문에서 제시하는 시작점은 여러 motion planning method 들이 제안되었음에도, 여전히 제한적인 환경에서는 비행하기 어렵다는 것이다.

Considerable motion planning methods

[4] Y. Li, G. Lu, D. He, and F. Zhang, “Robocentric model-based visual servoing for quadrotor flights,” IEEE/ASME Trans. Mechatron., vol. 28, no. 4, pp. 2155–2166, Aug. 2023.

[5] J. Yuan, “Hierarchical motion planning for multisteering tractor-trailer mobile robots with on-axle hitching,” IEEE/ASME Trans. Mechatron., vol. 22, no. 4, pp. 1652–1662, Aug. 2017.

[6] V. Usenko, L. V. Stumberg, A. Pangercic, and D. Cremers, “Real-time trajectory replanning for MAVs using uniform B-splines and a 3D circular buffer,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst., 2017, pp. 215222.

[7] H. Oleynikova, Z. Taylor, R. Siegwart, and J. Nieto, “Safe local exploration for replanning in cluttered unknown environments for microaerial vehicles,” IEEE Robot. Autom. Lett., vol. 3, no. 3, pp. 1474–1481, Jul. 2018.

[8] B. Zhou, J. Pan, F. Gao, and S. Shen, “RAPTOR: Robust and perceptionaware trajectory replanning for quadrotor fast flight,” IEEE Trans. Robot., vol. 37, no. 6, pp. 1992–2009, Dec. 2021.

[9] X. Zhou, Z. Wang, H. Ye, C. Xu, and F. Gao, “EGO-Planner: An ESDF-free gradient-based local planner for quadrotors,” IEEE Robot. Autom. Lett., vol. 6, no. 2, pp. 478–485, Apr. 2021.

[10] D. Mellinger and V. Kumar, “Minimum snap trajectory generation and control for quadrotors,” in Proc. IEEE Int. Conf. Robot. Autom., 2011, pp. 2520–2525.

[11] S. Liu et al., “Planning dynamically feasible trajectories for quadrotors using safe flight corridors in 3-D complex environments,” IEEE Robot. Autom. Lett., vol. 2, no. 3, pp. 1688–1695, Jul. 2017.

[12] C. Richter, A. Bry, and N. Roy, “Polynomial trajectory planning for aggressive quadrotor flight in dense indoor environments,” in Proc. Robot. Res.: 16th Int. Symp., 2016, pp. 649–666.

[13] J. Tordesillas, B. T. Lopez, M. Everett, and J. P. How, “FASTER: Fast and safe trajectory planner for navigation in unknown environments,” IEEE Trans. Robot., vol. 38, no. 2, pp. 922–938, Apr. 2022.

[14] F. Gao, L. Wang, B. Zhou, X. Zhou, J. Pan, and S. Shen, “Teach-repeatreplan: A complete and robust system for aggressive flight in complex environments,” IEEE Trans. Robot., vol. 36, no. 5, pp. 1526–1545, Oct. 2020.

[15] W. Ding, W. Gao, K. Wang, and S. Shen, “An efficient B-spline-based kinodynamic replanning framework for quadrotors,” IEEE Trans. Robot., vol. 35, no. 6, pp. 1287–1306, Dec. 2019.

[16] S. Liu, K. Mohta, N. Atanasov, and V. Kumar, “Search-based motion planning for aggressive flight in SE(3),” IEEE Robot. Autom. Lett.,vol.3, no. 3, pp. 2439–2446, Jul. 2018.

[17] G. Xu, Y. Chen, J. Cao, D. Zhu, W. Liu, and Y. Liu, “Multivehicle motion planning with posture constraints in real world,” IEEE/ASME Trans. Mechatron., vol. 27, no. 4, pp. 2125–2133, Aug. 2022.

[18] Y. Yan, L. Peng, J. Wang, H. Zhang, T. Shen, and G. Yin, “A hierarchical motion planning system for driving in changing environments: Framework, algorithms, and verifications,” IEEE/ASME Trans. Mechatron., vol. 28, no. 3, pp. 1303–1314, Jun. 2023.

실제로 safe flight corridor 에 의존하는 경로 생성 방식으로 인해 좁은 틈이나 복잡한 환경에서는 안전한 경로가 확보되기 어렵고, real-time replanning 이 어렵다!!

Time-optimal 을 고려하고자 한 선행 연구들로는 Scaramuzza 교수님 연구실에서 나온 [21] 과 [22] 가 있다.

Spatial-temporal optimization 을 같이 수행한 대표적인 연구인 Teach-repeat-replan [14] 도 있다. 하지만 이러한 방식들은 computationally expensive 한 단점이 있다.

Considering time optimality in optimization

[21] P. Foehn, A. Romero, and D. Scaramuzza, “Time-optimal planning for quadrotor waypoint flight,” Sci. Robot., vol. 6, no. 56, 2021, Art. no. eabh1221.

[22] R. Penicka and D. Scaramuzza, “Minimum-time quadrotor waypoint flight in cluttered environments,” IEEE Robot. Autom. Lett., vol. 7, no. 2, pp. 5719–5726, Apr. 2022.

[14] F. Gao, L. Wang, B. Zhou, X. Zhou, J. Pan, and S. Shen, “Teach-repeatreplan: A complete and robust system for aggressive flight in complex environments,” IEEE Trans. Robot., vol. 36, no. 5, pp. 1526–1545, Oct. 2020.

이러한 motion planner 들 중 좁은 틈을 잘 지나도록 한 선행 연구들도 제시하였는데, 이는 생략하고 흐름만 요약하도록 하자.

Liu et al. 등의 방법들과 narrow gaps 논문들도 있고 터널 환경을 지나기 위해 center line 을 뽑아서 경로를 계획하는 방식들도 있었다.

넓은 free space 확보를 위한 skeleton graph 방식들도 있는데 대표적으로는 generalized Voronoi diagram(GVD)-based 방법과 clustering-based 방법이 있다.

Skeleton graph methods in motion planning

[31] J. Wen, X. Zhang, H. Liu, H. Liu, J. Yuan, and Y. Fang, “G 2 VD Planner: An efficient motion planning approach with grid-based generalized Voronoi diagrams,” 2022, arXiv:2201.12981.

[32] C. Howie and B. Joel, “Sensor-based exploration: The hierarchical generalized Voronoi graph,” Int. J. Robot. Res., vol. 19, no. 2, pp. 96–125, 2000.

[33] D. Dolgov, S. Thrun, M. Montemerlo, and J. Diebel, “Path planning for autonomous vehicles in unknown semi-structured environments,” Int. J. Robot. Res., vol. 29, no. 5, pp. 485–501, 2010.

[34] H. Oleynikova, Z. Taylor, R. Siegwart, and J. Nieto, “Sparse 3D topological graphs for micro-aerial vehicle planning,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst., 2018, pp. 1–9.

[35] F. Blochliger, M. Fehr, M. Dymczyk, T. Schneider, and R. Siegwart, “Topomap: Topological mapping and navigation based on visual SLAM maps,” in Proc. IEEE Int. Conf. Robot. Autom., 2018, pp. 3818–3825.

[36] X. Chen, B. Zhou, J. Lin, Y. Zhang, F. Zhang, and S. Shen, “Fast 3D sparse topological skeleton graph generation for mobile robot global planning,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst., 2022, pp. 10283–10289.

[34] 에서는 ESDF 기반에서 3D GVD 를 만드는 방법론이 제안되었다. 그러나 ESDF 를 구성하고 저장하는 과정에서 많은 시간이 소요된다.

[35] 에서 clustering-based 방법이 제시되었는데, 이는 free space 를 여러 convex cluster 로 구성하여 skeleton graph 로 구성하는 방식이다. 하지만, cluster 의 convexity 를 확인하는 방식이 매우 time-consuming 하다는 단점이 있다.

Ray sampling 기반으로 빠르게 cluster 를 생성하는 [36] 은 accuracy 와 computational cost 사이의 밸런싱이 어렵다는 단점이 있다. 즉, 3D 환경에서 skeleton 을 얻어내는 것은 여전히 challenging 하다고 한다.

Skeleton-graph methods 를 이번에 알게 되어 자세한 연구 동향은 잘 모름.

여기서 제시된 EGO-Planner 는 soft constrained 방식으로 GCOPTER 에서 사용한 방식에 기반하였다. 그러나, 이 논문에서는 nonlinear optimization 이므로 local minima 에 빠질 수 있고, initial solution 에 민감하다고 지적하고 있다.

반면 hard-constrained 방식인 convex optimization(CO) 기반은 초창기부터 활발히 연구되어왔다. 앞선 방식에 비해 느리다는 단점이 있다고 알고 있다. 본 논문에서 제시한 문제점은 safety 가 hard constrained 로 고려되기 때문에 장애물과 너무 가깝게 경로가 생성될 수 있고, 실제 환경에서는 외란 등으로 인해 unsafe 할 수 있다고 한다.

따라서 본 논문은 위와 같은 문제점들을 해결하여 success rate, computational efficiency, minimum clearance 에서 우수함을 보인다고 한다.

Spatio-temporal Planning Framework

위 Fig. 1. 에 본 논문의 전체적인 구조가 제시되어 있다. 최근 대부분 연구들은 한번에 spatio-temporal optimization 을 수행하는데, 본 논문은 두 개의 sub-problem 으로 구분하여 별도로 optimization 하여 적은 constraints 와 dimension 을 가진다는 장점이 있다.

Question

• decouple 로 하면 효율적인 대신 sub optimal 한 것이 아닌지?
• 전체 problem 을 한번에 optimization 하지 않고 spatial 에 대해 먼저 optima 를 찾고 이에 대한 temporal 을 optimization 하는 것이 아닌가

Spatial planning 부분은 우리가 익숙히 알던 부분과 동일하다. A* 와 같은 searching-based method 로 초기 경로를 생성한다. 그리고 이 경로점들을 기반으로 flight corridor 를 생성한다.

본 논문에서는 fast sphere inflation-based skeleton extraction approach 라고 표현하였다. 그리고 unconstrained QP 를 풀어내 path smoothing 과정이 이루어진다.

이 최적화 과정에서 환경에 adaptive 하게 parameter tuning 이 이루어진다.

Temporal planning 에서는 최적화된 경로에 대해 time-optimal trajectory generation(TOTG) 방법을 통해 시간 최적화가 이루어진다. 하지만 강건하지 않아 실패할 경우에 trapezoidal velocity profile 이 사용된다.

TOTG

[40] T. Kunz and M. Stilman, “Time-optimal trajectory generation for path following with bounded acceleration and velocity,” in Proc. Robot.: Sci. Syst. VIII, 2012, pp. 1–8.

보다시피 기존 motion planner 와 다른 점은 skeleton approach, adaptive parameter tuning, TOTG 정도가 있겠다.

Fast Sphere Inflation-based Skeleton Extraction

본 논문에서 contribution 으로 제시하는 skeleton extraction 은 선행 연구들처럼 GVD 나 clustering 방식이 아니라, 초기 경로를 장애물로부터 멀리 밀어내면서 생성하기 때문에 훨씬 빠르게 생성할 수 있다고 한다.

주요 생성 방식은 그림을 통해 설명한다.

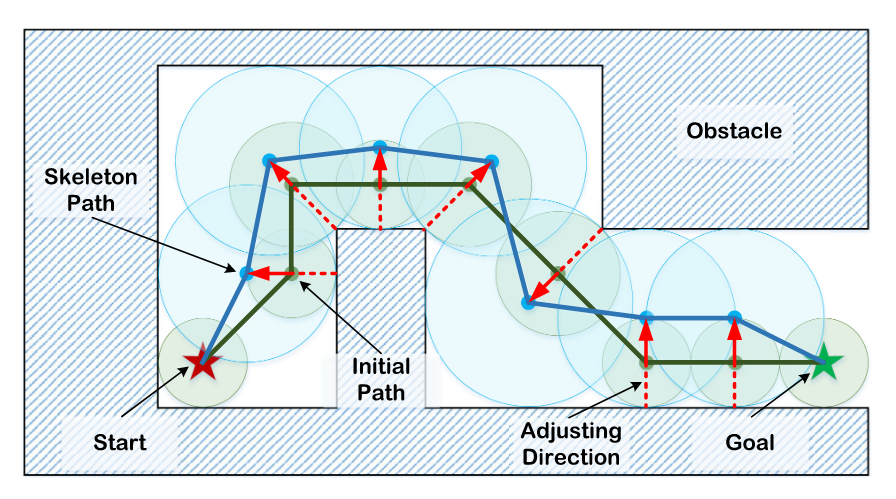
free space $\mathcal{F}$ 에서 중심 $\mathbf{p}$ 와 반지름 $r$ 로 safe sphere $S(\mathbf{p},r)$ 을 정의할 수 있다. 이 때, 가장 가까운 장애물을 통해 최대 크기의 구체 $S_{max}(\mathbf{p})$ 이 정의된다.

경로 생성에서 초기값으로 주어지는 start ${\mathbf{p}}_s$ 와 goal ${\mathbf{p}}_g$ 를 제외하고 나머지 경로점들은 $S_{max}$ 의 끝지점으로 이동한다. 이 때, 가장 가까운 장애물 점의 반대 방향으로 이동하여 높은 clearance 를 확보한다.

새로운 장애물로 인해 더이상 확장되거나 이동할 수 없을 경우 반복과정이 중단된다.

A. Fast Skeleton Waypoints Extraction

앞선 내용을 요약하면 maximum safe sphere generation 과 point adjustment 가 반복되며 이루어진다. 이 때의 adjusting direction $\mathbf{d}({\mathbf{p}}^l)$ 을 수식적으로 정의하고, 보다 효율적인 방식을 위해 어떤 practical 한 방식을 사용하는지 알아보자.

resolution $\delta$ 를 갖는 discrete voxel map $\mathcal{M}$ 을 가질 때, maximum sphere $S_{max}(\mathbf{p})$ 를 얻기 위해 $\delta$ 만큼 증가하면서 충돌 여부를 탐색한다.

만약, $h+1$ 번 째 voxel 표면에서 충돌이 일어나면 $(h+1)\delta$ 반지름을 갖는 구체에서 충돌이 일어났으므로 $S_{max}$ 의 반지름 $r_{max}(\mathbf{p})$ 는 $h\delta$ 값을 갖는다. (i.e. $S_{max}(\mathbf{p},r_{max})=S_{max}(\mathbf{p},h\delta )$)

point adjustment 는 기존 $\mathbf{p}$ 에서 가까운 장애물의 반대 방향으로 이루어진다.

$m$ 개의 가까운 장애물 ${\mathbf{O}}^l$ 을 다음과 같이 정의한다.

$${\mathbf{O}}^l=\{o_j^l|j=1,\dots ,m\},\text{where}{o}_j^l\notin \mathcal{F}\text{(free space)}$$

이 의미는 occupied voxel 이라는 의미와 같다.

그렇다면 각 장애물 $o_j^l$ 로 부터 얻어지는 방향을 아래와 같이 정의할 수 있으므로, adjusting direction $\mathbf{d}({\mathbf{p}}^l)$ 도 정의된다.

$$\begin{array}{rl}\mathbf{d}({\mathbf{p}}^l,{\mathbf{o}}_j^l)& =\frac{p^l-o_j^l}{\Vert p^l-o_j^l\Vert },j\in \{1,\dots ,m\}\\ \mathbf{d}({\mathbf{p}}^l)& =\frac{{\sum }_{j=1}^m\mathbf{d}({\mathbf{p}}^l,{\mathbf{o}}_j^l)}{m}\end{array}$$

장애물이 adjusting direction 의 반대 방향에 존재 하는 경우, 즉, $\mathbf{d}({\mathbf{p}}^{l-1})\cdot \mathbf{d}({\mathbf{p}}^l,\mathbf{o})<0,\forall \mathbf{o}\in {\mathbf{O}}^l$ 으로 표현할 수 있다.

전체 알고리즘 요약은 위와 같다. 또한 매번 방향을 계산하는거는 많은 계산을 소요하므로 line 3 에서 결정된 adjusting direction 은 고정되어 line 6, 7 과정을 수행한다.

그리고 $r_{init}=0$ 으로 시작하면 voxel 을 매 $\delta$ 마다 체크해야 하므로, 초기 $r_{init}({\mathbf{p}}^l)$ 을 아래와 같이 설정한다.

$$r_{init}({\mathbf{p}}^l)=r_{max}({\mathbf{p}}^{l-1})-\Vert {\mathbf{p}}^l-{\mathbf{p}}^{l-1}\Vert ,l>0$$

즉, 이전 위치와의 최대 반지름과 거리 차 안에서는 path searching 으로 $S_{(}{\mathbf{p}}^l,r_{init})\subset \mathcal{F}$ 가 보장된다.

B. Skeleton Path Pruning and Interpolation

앞선 알고리즘 만으로는 특정한 케이스에서 safety 와 optimality 가 보장되지 않는다. 따라서 이를 해결하기 위한 heuristic 한 방식으로 pruning 과 interpolation 을 통해 이러한 케이스들을 해결하고자 했다.

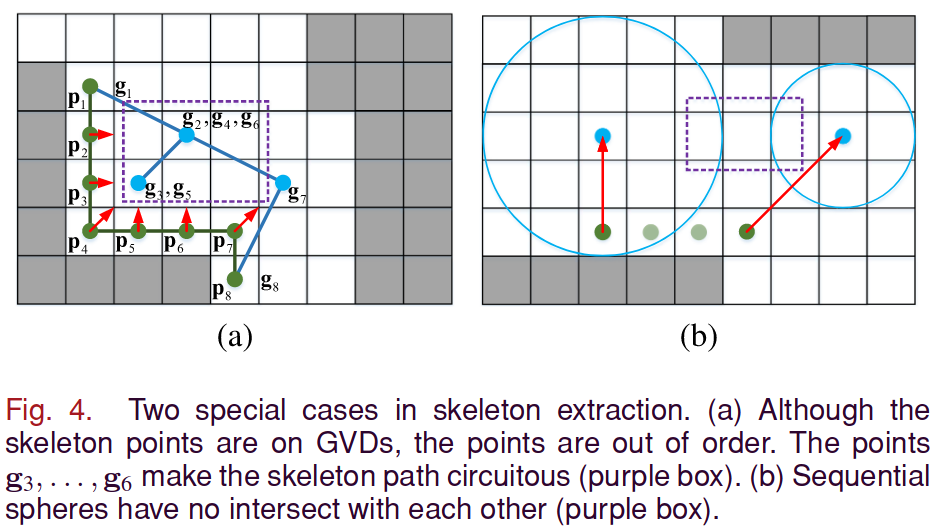
위 그림의 (a) 의 경우에는 $\mathbf{p}$ 가 밀집하게 구성되어 있어 이동된 $\mathbf{g}$ 가 circular 하게 생성되었다. 이를 위해 pruning 이 적용된다.

본 논문에서는 $\Vert {\mathbf{p}}_i-{\mathbf{g}}_{last}\Vert \le \alpha r_{last}$ 이거나 $\Vert \mathbf{g}-{\mathbf{g}}_{last}\Vert \le \alpha (r_{last}-r)$ 인 경우에 $\mathbf{p}$ 나 $\mathbf{g}$ 를 버린다.

그리고 앞선 방식과 pruning 을 통해 만들어진 ${\mathbf{g}}_i$ 와 ${\mathbf{g}}_{i+1}$ 이 너무 멀리 떨어져 위 그림의 (b)와 같이 intersection 이 생기지 않을 수 있다.

이러한 경우에는 ${\mathbf{g}}_i$ 와 ${\mathbf{g}}_{i+1}$ 사이의 직선이 safe 한 경우 interpolation 을 수행하고, 그렇지 않은 경우에는 기존의 $\mathbf{p}$ 를 바로 interpolation 한다.

전체 알고리즘은 아래와 같다. 주요하게는 line 5, 7, 10-12 를 보면 된다.

Question

• 직접 코드로 짜봐야 알겠지만, path-searching 으로 얻은 $\mathbf{p}$ 에서 extractSkeletonWaypoint() 도 수행하는데 safeLine() 이 되지 않는 경우도 생기는지?
• $\alpha$ 의 영향으로 예외적인 케이스가 있을건지?

Skeleton-guided Path Smoothing with Environmental Adaptive Parameter Tuning

이제 만들어진 skeleton graph 와 safety bubble 들을 가지고 path smoothing 이 어떻게 이루어지는지 알아보자.

A. Problem Formulation

Given the skeleton $\mathbf{G}=\{g_i|i=1,\dots ,n\}$ and corresponding spheres $\mathbf{S}=\{{\mathcal{S}}_i|i=1,\dots ,n\}$

Generate a safe and smooth path $\mathbf{X}=\{{\mathbf{x}}_i|i=1,\dots ,n\}$

$$\begin{array}{rl}& \min J_s(\mathbf{X})\\ \text{s.t}& \mathbf{AX}=\mathbf{w}\\ & {\mathbf{x}}_i\in {\mathcal{S}}_i,i\in \{1,\dots ,n\}\end{array}$$

여기서 $\mathbf{w}$ 는 시작점과 목표점을 포함한 반드시 지나야 하는 경로점을 의미한다. 따라서 $\mathbf{A}$ 는 waypoints constraints 에 해당하는 행렬이 된다.

본 논문에서는 목적함수 $J_s(\mathbf{X})$ 를 elastic band 로 정의하였다.

Elastic bands

• S. Quinlan and O. Khatib, “Elastic bands: connecting path planning and control,” [1993] Proceedings IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 1993, pp. 802-807 vol.2, doi: 10.1109/ROBOT.1993.291936.

$$J_s(\mathbf{X})=\sum _{i=2}^{n-1}(\Delta x_{i+1}-\Delta x_i{)}^T(\Delta x_{i+1}-\Delta x_i)$$

장애물 회피를 위한 safety constraints 는 아래와 같이 정의된다.

$$(x_i-g_i{)}^T(x_i-g_i)\le r_i^2,i\in \{1,\dots ,n\}$$

논문에서 $g_i$ 는 skeleton waypoint $\mathbf{G}$ 뿐만 아니라 ${\mathcal{S}}_i$ 의 중심도 포함된다고 말하고 있는데, 둘이 같은 것이 아닌지?

boundary constraints 는 별개로 얻어진다고 한다. velocity direction 은 $x_0$ 과 $x_{n+1}$ 을 도입하여 아래와 같이 정의한다.

$$x_o=p_s-\delta \frac{v_s}{\Vert v_s\Vert },x_{n+1}=p_e-\delta \frac{v_e}{\Vert v_e\Vert }$$

velocity value 를 temporal planning 에서 결정된다.

지금까지의 목적함수와 제한조건을 통해 QCQP 로 문제를 정의할 수 있다.

B. Skeleton-Guided Optimization with Closed-form Solutions

모든 free space 가 동일하게 여겨지기 때문에 이러한 QCQP 를 풀고나면 장애물과 매우 가깝게 경로가 생성될 수 있다.

그래서 본 논문에서는 추가적인 목적함수 $J_g(\mathbf{X})$ 를 도입하여 skeleton $\mathbf{G}$ 와 최적 경로 $\mathbf{X}$ 와의 거리를 줄이고자 하였다.

$$J_g(\mathbf{X})=\sum _{i=1}^n(x_i-g_i{)}^T(x_i-g_i)$$

이러한 목적함수는 high clearance 를 갖는 $\mathbf{G}$ 에 가까운 $\mathbf{X}$ 를 생성하여 safety constraints 를 없앨 수 있게 된다.

그에 따라 새로운 목적함수 $J$ 를 아래와 같이 정의한다.

$$\begin{array}{rl}J& =J_s(\mathbf{X})+\kappa J_g(\mathbf{X})\\ & ={\mathbf{X}}^T{\mathbf{Q}}_s\mathbf{X}+\kappa {\mathbf{X}}^T\mathbf{X}+\kappa {\mathbf{G}}^T\mathbf{X}\end{array}$$

이 때 ${\mathbf{Q}}_s$ 는 smoothness 의 역할을 하고 (like minimum snap) $\kappa$ 는 skeleton guidance weight 로 $J_g$ 의 중요도를 조절한다.

본 논문에서는 위 내용에 문제가 있는데 $J_g(\mathbf{X})={\sum }_{i=1}^n(x_i-g_i{)}^T(x_i-g_i)$ 가 quadratic form 으로 정리될 때 ${\mathbf{G}}^T\mathbf{X}$ 가 아니라 $-{\mathbf{G}}^T\mathbf{X}$ 가 되어야 한다.

$J_g$ 를 quadratic form 으로 정리하면 ${\mathbf{X}}^T\mathbf{X}-2{\mathbf{G}}^T\mathbf{X}+{\mathbf{G}}^T\mathbf{G}$ 가 되는데 마지막 term 은 상수이므로 최적화 단계에서 무시할 수 있다. 그러나 ${\mathbf{X}}^T\mathbf{X}$ 와 ${\mathbf{G}}^T\mathbf{X}$ 의 부호가 다르기 때문에 같은 $\kappa$ 로 묶을 때 부호와 스케일을 정확히 고려해주어야 한다.

$$\begin{array}{rl}J& =J_s(\mathbf{X})+\kappa J_g(\mathbf{X})\\ & ={\mathbf{X}}^T{\mathbf{Q}}_s\mathbf{X}+\kappa {\mathbf{X}}^T\mathbf{X}-2\kappa {\mathbf{G}}^T\mathbf{X}\end{array}$$

목적함수의 최적화 방향을 도식화하면 아래와 같다.

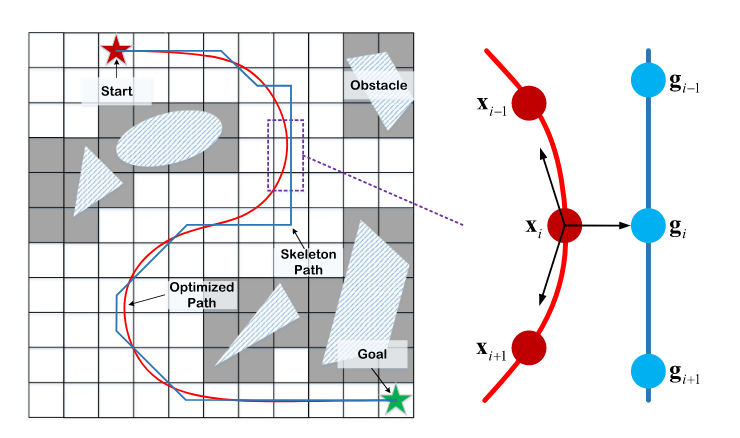
Question

• 이전의 minimum snap 은 최적제어에서 Minimum Effort Problem 에서부터 유도된 것인데, 단순히 상대거리 최소화와 높은 clearance 로 목적함수를 두는 것이 충분한 최적 경로인가?
• 이전의 경로 생성 문제들은 safety constraints 가 nonlinear 함으로 인해 풀기 어려웠던 것인데, 그냥 목적함수에 넣어서 해도 되는것인지?
• 추후 temporal optimization 을 봐야 하겠지만 minimum time 이 잘 될 수 있을지 봐야할듯

이제 이를 통해 closed-form solution 을 구해보자.

$$\mathbf{X}=\mathbf{M}\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right],\mathbf{M}={\mathbf{A}}^{-1}\mathbf{C}$$

이 때 $\mathbf{C}$ 는 elementary matrix 이다. 이전에 polynomial trajectory 생성 논문들에서 주로 $\mathbf{AM}=\mathbf{C}$ 로 하여 coefficient $\mathbf{C}$ 를 얻기 위한 mapping matrix $\mathbf{M}$ 을 definite 하게 찾았는데 이와 유사한 것으로 이해했다.

notation ${\mathbf{w}}_f$ 와 ${\mathbf{w}}_p$ 는 각각 fixed and free derivatives 이다.

위에서 정의한 $\mathbf{X}$ 를 앞선 $J$ 에 대입하여 표현해보자.

$$\begin{array}{rl}J& ={\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]}^T{\mathbf{M}}^T{\mathbf{Q}}_s\mathbf{M}\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]+\kappa {\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]}^T{\mathbf{M}}^T\mathbf{M}\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]-2\kappa \mathbf{GM}\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]\\ & ={\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]}^T{\mathbf{M}}^T({\mathbf{Q}}_s+\kappa I)\mathbf{M}\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]-2\mathbf{K}\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]\\ & ={\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]}^T\mathbf{R}\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]-2\mathbf{K}\left[\begin{array}{c}{\mathbf{w}}_f\\ {\mathbf{w}}_p\end{array}\right]\end{array}$$

논문에서 문제되는 부분을 수정해서 수식을 다시 정리하였다.

앞서 elastic bands 로 표현되는 $J_s$ 를 통해 ${\mathbf{Q}}_s$ 는 symmetric matrix 임을 알 수 있고, $\mathbf{R}=\left[\begin{array}{cc}{R}_{ff}& R_{fp}\\ R_{pf}& R_{pp}\end{array}\right]$ 로 나타낼 수 있고 $\mathbf{K}={\left[\begin{array}{c}{\mathbf{K}}_f\\ {\mathbf{K}}_p\end{array}\right]}^T$ 와 같다.

여기서 또 의문점은 $\kappa$ 로 엮이는 부분을 $R$ 과 $K$ 로 나눠서 표현해도 되는 것인가 하는 것이다.

이제 $w_p$ 에 대한 $J$ 의 Jacobian 을 계산해보면 아래와 같다.

$$\frac{\partial J(\mathbf{X})}{\partial {\mathbf{w}}_p}=2{\mathbf{R}}_{pf}{\mathbf{w}}_f+2{\mathbf{R}}_{pp}{\mathbf{w}}_p-2{\mathbf{K}}_p$$

논문에서는 $+{\mathbf{K}}_p$ 로 구성되어 계수 $2$ 를 지워낼 수 없지만 이 유도에서는 계수를 생략할 수 있다.

Jacobian 을 0으로 만듦으로써, optimal free derivatives ${\mathbf{w}}_p^{\ast }$ 를 아래와 같이 얻어낼 수 있다.

$${\mathbf{w}}_p^{\ast }=-{\mathbf{R}}_{pp}^{-1}({\mathbf{K}}_p+{\mathbf{R}}_{pf}{\mathbf{w}}_f)$$

C. Environmental Adaptive Parameter Tuning

Environment 에 adaptive 하게 경로를 조정하는 것은 되게 좋은 아이디어라고 여겼고, 러닝 기반으로 접근할 수도 있겠다는 생각을 했으나 본 논문에서의 용어는 일반적인 이해와는 약간 차이가 있다.

앞서 safety constraints 대신 $J_g$ 를 사용하기 때문에 안정성이 보장되기 어렵다.

그래서 $\kappa$ 를 adaptive 하게 조정한다고 한다.

$\kappa$ 가 작을 수록 smooth 한 경로가 생성되고 ${\kappa }_{min}$ 에서도 safety 는 보장되어야 한다. 본 논문에서는 ${\kappa }_{min}$ 과 ${\kappa }_{max}$ 사이에서 $\log$ 스케일로 결정되기를 원했고 아래와 같이 수식을 구성하여 $\kappa$ 를 결정한다.

$$\log (\kappa )=\frac{\log ({\kappa }_{low})+\log ({\kappa }_{high})}{2},\therefore \kappa \sqrt{{\kappa }_{low}{\kappa }_{high}}$$

구체적인 adaptive parameter tuning 방법은 아래 알고리즘에 표현되어 있다.

그래서 $\mathbf{X}$ 의 최소 안전 거리가 $\beta \min \{\mathbf{r}\}$ 보다 작은 경우 unsafe 로 여긴다. $\beta \in (0,1)$ 은 safety ratio 이다.

Question

• $\mathbf{X}$ 의 최소 안전거리를 어떻게 알아낼 것인가? 이전의 $\mathbf{r}$ 을 사용하지 않고 얻어낸다는 것인데 전체 경로에 대해 다시 체크를 수행할 것인지?
• $\beta$ 를 사용하는 것이 굉장히 experimental 하다. 물론 safe margin 을 위해서 필요하긴 할 것…
• 왜 $\log$ 로 $\kappa$ 를 정할까

D. Trajectory Generation

여태까지는 time allocation 을 고려하지 않았다. 본 논문에서는 생성된 경로에 대해 TOTG 를 수행한다고 한다. 그러나 종종 이 방식이 실패하기 때문에 backup 전략으로 trapezoidal velocity profile 로 시간을 할당한다.

TOTG

[40] T. Kunz and M. Stilman, “Time-optimal trajectory generation for path following with bounded acceleration and velocity,” in Proc. Robot.: Sci. Syst. VIII, 2012, pp. 1–8.

여기서 또 궁금증은 앞서서 목적함수에서 시간 관련을 아예 빼버렸기 때문에 optimal time 이 되지 않는 경로인데, backup 으로 trapezoid velocity 방식이 사용되면 전체 도달 시간 측면에서는 성능이 좋지는 않을 것 같다.

Simulations and Experiments

필요한 내용만 요약해서 정리.

본 논문에서는 clearance & safety 에 집중하였기 때문에 관련한 평가지표를 구성하여 선행 연구들과 비교하였다.

Average clearance of path $\mathbf{P}$ 를 아래와 같이 주변 장애물과의 평균 거리로 구성하였다.

$$d_{avg}(\mathbf{P})=\frac{{\sum }_{i=1}^{n^{\prime }}\text{nearestDist}({\mathbf{p}}_i,\mathcal{M})}{n^{\prime }}$$

A. Implementation Details

III. B. 에서 사용한 maximum intersection ratio $\alpha$ 는 0.7, III. C. 에서 사용한 safey ratio $\beta$ 는 0.8, 최대 iteration은 5, parameter tuning 을 위한 ${\kappa }_{max}=0.5$, ${\kappa }_{min}=5\times 10^{-4}$ 이다.

Voxel map $\mathcal{M}$ 의 resolution $\delta =0.1\text{m}$ 이고, $v_{max}=1.5m/s$, $a_{max}=1.0m/s^2$ 이다.

B. Simulations

https://github.com/HKUST-Aerial-Robotics/mockasimulator

위 환경 구성을 활용함. 시뮬에서는 A* 와 최신 skeleton graph 생성 연구, 본인들의 제안방식을 비교하였음.

그리고 Teach-repeat-replan 과 EGO-Planner 를 각각 global, local planning SOTA 로 선정하여 본인들의 방식과 비교하였음.

놀라운 점은 time-optimal 을 고려하지 않아 최단속도 보장이 어려울 것이라고 생각했는데 Trajectory duration 도 더 짧은 경우가 많았고, 연산 시간도 매우 단축되었다. 그리고 SFC 생성 방식의 단점대로 EGO-Planner 는 좁은 환경에서 안전한 경로를 만드는데 여러 번 최적화를 수행해 시간이 오래 걸린다고 하였다.

다만 아쉬운 점은 $v_{max}$ 가 너무 낮아서 빠른 비행에서는 어떨지 궁금하다. (Bubble Planner 는 $v=10m/s$ 에서 테스트하였음.)

Conclusion

기존과 차이가 없는듯 하면서도 신선한 접근법들이 많이 사용된 플래너 였다.

기존의 SFC 대신 skeleton graph 라는 용어를 사용한 것이 신선하고, 굉장히 simple 한 방식으로(어쩌면 누군가는 practical 하게 해봤을 법도 한) 시간을 많이 단축시킨 것이 좋았다.

하지만 기존에 알고 있던 접근과 달라서 의문인 부분들도 많았다.

목적함수를 저렇게 구성해도 최적임이 보장되나? nonlinear opt. 방식이 local optima 라고 지적하면서 $\kappa$ 를 iterative 하게 적당히 찾아서 만드는게 맞나?

Sphere 들 사이에 intersection 에 반드시 $\mathbf{w}$ 를 넣은 것이 아님에도 clearance 로만 잘 회피해도 충분한가?

어쩌면 기존 방법들은 너무 최적최적하는 것에 집중해서 그럴지도 모르겠다. optima 대신 iteration 으로 clearance 확보한 경로를 만드는 것이 본 논문이 주장하는 narrow 한 환경에서도 매우 safe 한 경로에는 더 좋았을 수 있겠다. (thus, success rate looks higher than prev. methods)

그럼에도 본 논문의 목적함수 구성 방식과 skeleton-graph 방식은 특정 목적에 매우 효과적인 Planner 를 만드는데 좋아보인다.

이상 끝.