[RA-L '18] Search-Based Motion Planning in SE(3)

Search-Based Motion Planning for Aggressive Flight in SE(3)

Cite

• Liu, Sikang, et al. “Search-based motion planning for aggressive flight in se (3).” IEEE Robotics and Automation Letters 3.3 (2018): 2439-2446.

Arxiv

논문 복습 겸 정리 // 수식은 논문 번호를 따라가되, 인용 논문은 순서대로 표기함.

Abstract

Aerial Vehicle 중 Multi-rotor의 Whole-body motion planning을 다룬 논문 중 하나이다. 주로 위치, 속도, 가속도 제어를 하는 것과 달리 jerk, snap의 제어 혹은 yaw에 더해 roll, pitch까지 제어하는 것은 고연산을 요하기에 기체의 모델을 Sphere, Prism(각기둥)으로 가정한다.

이러한 방식은 collision-free한 영역을 확인하는 과정에서 constraint 조건을 손쉽게 만들어준다.

주요 Contributions

• 기체를 ellipsoid로 가정하여 모델링함
• lower dimension에서 경로를 탐색한 후 이를 heuristic으로 사용하여 higher dimension에서의 경로 탐색에 활용
• Optimal control problem을 풀어 낸 state들이 이루는 motion primitives를 graph search algorithm을 통해 dynamically feasible resolution-complete한 경로를 만든다
• 이러한 과정에서의 생성된 궤적의 타당성, 연산 시간, 가중치 변수 등의 실험 결과도 보여줌

요약하자면, Model dynamics, Collision-free 등의 constraint를 고려한 OCP를 풀어 내고 이를 통해 구성된 motion primitives를 graph search algorithm과 hierarchical한 방식으로 적절한 computational time과 control effort를 가지는 경로를 생성한다.

논문에서는 Jerk 제어까지 실험한 내용들을 다루었으며 Snap 제어에 대해서는 같은 방식으로 이루어지며 공개한 코드에서 확인할 수 있다고 언급만 되어있다.

Related Works

Sampling 방식을 사용한 Planning with 6 DOF는 여러 연구에서 진행되었지만, MAV는 rotation과 translation이 독립적으로 이루어질 수 없어 적용할 수 없다.

이에 Motion primitives를 이용한 방식을 통해 dynamically feasible하고 collision-free한 경로 생성한다.

Lattice search를 이용한 선행 연구들 [1-2] 중 Optimal control problem을 통해 만든 motion primitives를 활용한 본인의 연구 [3]를 확장한 것이 본 논문이다.

Cite

[1] M. Pivtoraiko, R. A. Knepper, and A. Kelly, “Differentially constrained mobile robot motion planning in state lattices,” Journal of Field Robotics, vol. 26, no. 3, pp. 308–333, 2009.

[2] B. MacAllister, J. Butzke, A. Kushleyev, H. Pandey, and M. Likhachev, “Path planning for non-circular micro aerial vehicles in constrained environments,” in Robotics and Automation (ICRA), 2013 IEEE International Conference on. IEEE, 2013, pp. 3933–3940.

[3] Liu, Sikang, et al. “Search-based motion planning for quadrotors using linear quadratic minimum time control.” 2017 IEEE/RSJ international conference on intelligent robots and systems (IROS). IEEE, 2017.

또한, [3]에서 참고한 Optimal control 논문은 T-RO 논문인 [4] 이다. (추후 훑어볼 것!!)

Cite

[4] M. Mueller, M. Hehn, and R. D’Andrea, “A computationally efficient motion primitive for quadrocopter trajectory generation,” IEEE Trans. on Robotics (T-RO), vol. 31, no. 6, pp. 1294–1310, 2015.

대부분 시간에 대한 state $x(t)$ 로 이루어진 다항식으로 경로를 생성하므로 state의 dimension이 커질수록 높은 연산량을 요구한다.

이에 대해 Randomized sampling 방식과 Graph search 방식을 고려할 수 있다. 전자는 효율적이지만 optima로의 느린 수렴 속도로 인해 빠른 navigation과 re-planning에는 부적합하다.

후자는 비효율적이나 heuristic한 방식을 통해 이를 개선할 수 있다. weighted heuristic 방식 대신 adaptive dimension을 활용한 방식을 적용하여 본 논문에서는 hierarchical planning procedure를 도입하였다.

Motion Planning with Attitude Constraints

앞선 논문 [3]을 통해 만들어진 motion primitives를 이용해 trajectory planning framework에 대한 설명이 이루어진다.

이 때, quadrotor의 yaw는 decoupled되어 있고 system dynamics에 영향을 주지 않으므로 상수로 가정한다. (=heading을 진행 방향과 일치시키지 않는다는 의미 = simpler)

Note

• yaw도 dynamics에 고려한 경로 계획 논문이 있을까?

A. System Dynamics

Quadrotor의 dynamics는 ${\mathbb{R}}^3$ 에서 differentially flat 함이 증명되었다. [5] 따라서 position $\mathbf{x}=[x,y,z{]}^T$ 를 시간에 대한 미분인 속도, 가속도, jerk로 표현한 경로 생성과 제어에 관한 선행 연구들 [6-7]을 통해 Model dynamics를 전개하였다.

Cite

[5] D. Mellinger and V. Kumar, “Minimum snap trajectory generation and control for quadrotors,” in Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), 2011.

[6] T. Lee, M. Leoky, and N. H. McClamroch, “Geometric tracking control of a quadrotor UAV on SE(3),” in 49th IEEE Conference on Decision and Control (CDC). IEEE, 2010, pp. 5420–5425.

[7] M. Hehn and R. D’Andrea, “Quadrocopter trajectory generation and control,” IFAC Proceedings Volumes, vol. 44, no. 1, 2011.

추후 훑어볼 것…

Todo

• Lattice search
• 논문 [4-7] 리뷰

구체적인 수식 전개는 이미지로 대체, Quadrotor dynamics에 대한 내용은 notation의 차이는 있지만 Rotor drag까지 고려한 M. Fasessler, et al 외에는 대체로 동일하다.

Todo

• 논문 [6]과 같이 SO(3)에서의 orientation 수식 전개

Note

• Rotor drag까지 고려하는 방식의 Motion planning도 있나?

B. Search-Based Planning Using Motion Primitives

Differential flatness한 system에서 경로 $\Phi (t)=[{\mathbf{x}}^T,{\mathbf{v}}^T,{\mathbf{a}}^T,{\mathbf{j}}^T]$ 로 구성되고 이는 time $t$ 에 대한 다항식으로 각각 표현할 수 있다.

$$\mathbf{x}(t):=\sum _{k=0}^K{\mathbf{d}}_k\frac{t^k}{k!}={\mathbf{d}}_K\frac{t^K}{K!}+\cdots +{\mathbf{d}}_{1}t+{\mathbf{d}}_0\text{\hspace{1em}(8)}$$

${\mathbf{d}}_k\in {\mathbb{R}}^3$ 는 계수이고, 위 식을 미분함으로써 속도, 가속도, jerk, snap에 대한 다항식을 얻어낼 수 있다.

특정한 시간 간격에서 한 state에서 다른 state 간의 다항식 경로를 motin primitive라고 한다.

따라서 각 state에서는 control $u$ 에 따른 다음 state가 생겨나며 initial state와 goal state 간에는 여러 sequence의 motion primitives가 존재한다. 이를 graph로 구성하여 search algorithm을 통해 optimal sequence를 찾아내는 것이 본 논문의 주 요지이다.

본 논문은 jerk $j$ 를 control input으로 사용하여 optimal trajectory ${\Phi }^{\ast }(t)$ 를 생성하므로 state $s(t)$ 는

$$s(t)=[p^T,v^T,a^T{]}^T\text{\hspace{1em}(9)}$$

이다.

pre-defined control set ${\mathcal{U}}_M$ 에서의 constant jerk input ${\mathbf{u}}_m$ 을 initial state ${\mathbf{s}}_0$ 에 가해 만들어진 curve는 $t\in [0,\tau ]$ 에서의 motion primitive 이다. 이를 수식화하면 아래와 같다.

$$s(t)=F({\mathbf{u}}_m,{\mathbf{s}}_0,t):=\left[\begin{array}{c}{u}_m\frac{t^3}{6}+a_0\frac{t^2}{2}+v_{0}t+p_0\\ u_m\frac{t^2}{2}+a_{0}t+v_0\\ u_{m}t+a_0\end{array}\right]\text{\hspace{1em}(10)}$$

요약하면 differential flatness한 state에 대해 jerk $j$ 대신 control input $u_m$ 으로 수식화한 것이다.

이 때 $F(\cdot )$ 은 주어진 $u_m,s_0,t$ 에 대해 minimum jek trajectory를 만드는 함수이다. [3-4]

control input set ${\mathcal{U}}_M$ 과 $\tau$ 에서 graph $\mathcal{G}(S,\mathcal{E})$ 를 정의한다. $S$ 는 $s_0$ 부터 가능한 모든 state의 집합이다. ( $\therefore S\subset {\mathbb{R}}^9$) $\mathcal{E}$ 는 각 state들을 연결하는 edge의 집합이며 이 때 edge는 motion primitive와 같다.

앞선 [3]에서 initial state $s_0$ 부터 goal state $s_g$ 까지 경로 탐색 문제를 total control effort $J$ 와 time $T$ 를 통해 아래와 같이 정의했다.

a desired optimal trajectory ${\Phi }^{\ast }(t)$

$$\begin{array}{r}{\Phi }^{\ast }(t)=\arg \underset{\Phi (t)}{\min }J+\rho T\\ s.t.s_0\leftarrow \Phi (0),s_g\leftarrow \Phi (T)\end{array}\text{\hspace{1em}(11)}$$

이 때 $T=\tau$ 이고 이에 따라 $J={\int }_0^T\Vert j{\Vert }^{2}dt=\Vert u_m{\Vert }^2\tau$ ($\because$ constant jerk input $u_m$ ) 이다.

따라서 state $s_n$ 에서 $u_m$ 을 가한 primitive(=curve =trajectory)의 cost function $C(\cdot )$ 은 아래와 같이 정리된다.

$${\Phi }^{\ast }(t)=\arg \underset{\Phi (t)}{\min }C(s_n,u_m)$$ $$s.t.C(s_n,u_m)=C(u_m)=(\Vert u_m{\Vert }^2+\rho )\tau \text{\hspace{1em}(12)}$$

*Pontryagin’ minimum principle*에 의해 식 (10)은 식 (11)의 optimal solution 이다. 따라서 식 (11)을 푸는 것은 아래의 deterministic shortest path problem의 최적해를 찾는 것과 같다. (= 아래 problem의 optima = optimal trajectory)

Todo

• Pontryagin’ minimum principle과 선행 논문 [3] 증명 정리

Problem 1

주어진

• An initial state ${\mathbf{s}}_0$
• A goal region ${\mathcal{X}}^{goal}$
• A free space ${\mathcal{X}}^{free}$
• Motion primitives $F_n(t)$ based on a finite set of control inputs ${\mathcal{U}}_M$ with duration $\tau >0$

에 대해 $0$ 부터 $N-1$ 까지의 control inputs ${\mathbf{u}}_i$ 를 선택하는 것은 아래와 같이 정리된다.

$$\begin{array}{rl}\underset{N,{\mathbf{u}}_{0:N-1}}{\min }& (\sum _{n=0}^{N-1}\Vert u_n{\Vert }^2+\rho N)\tau \\ s.t.F_n(t)& :=F(u_n,s_n,t),u_n\in {\mathcal{U}}_M\\ s_{n+1}& =F_n(\tau )=F_{n+1}(0),s_N\in {\mathcal{X}}^{goal}\\ F_n(t)& \subset {\mathcal{X}}^{free}\end{array}\text{\hspace{1em}(13)}$$

요약하면, 주어진 $s_0$ 부터 $s_N$ 까지 cost function $C(s_n,u_m)$ 을 최소화하며 motion primitives와 collision-free를 만족하는 control input $u_n$ 의 조합을 찾는 것이다.

본 논문은 이 문제를 ${\text{A}}^{\ast }$ 와 같은 그래프 탐색 알고리즘을 해결한다.

Note

• 그래프 탐색보다 효율적인 방식으로 궤적을 생성하는 것은 어떨까
• 혹은 ${\mathbf{A}}^{\ast }$ 보다 좋은 방식은 없을까

기존의 distance-based heuristic은 속도, 가속도 혹은 방향을 급격하게 바뀔 수도 있는 경로 계획에서는 부적합하여 논문 [3]에서 제시한 방식을 사용한다.

이 방식은 Linear Quadratic Minimum Time 문제의 해와 trajectory smoothness를 고려한다.

LQMT 의 해는 heuristic function $H(s,s_g)$ 의 explicit formula를 제공한다. (이 때, $s$ 와 $s_g$ 는 각각 현재 state와 목표 state 이다.)

C. Feasibility Checking

Problem 1에서 $F_n(t)\subset {\mathcal{X}}^{free}$ 는 system dynamics와 장애물에 의한 geometric constraints로 나눠 고려할 수 있다.

1) Dynamically Feasible Primitives Quadrotor에서 dynamic constraints는 각 모터에 의해 생기는 thrust와 torque에 최소/최대값이나 각 기체마다 따져보는 것과 적절한 비선형적인 constraints를 적용하는 것이 어렵다. 추가자료

따라서 differential flatness를 이용해 속도, 가속도, jerk 에 대해 적용하는 것이 훨씬 합리적이다. 이를 수식으로 정리하면 아래와 같다.

$$|\dot{\mathbf{x}(t)}|\le {\mathbf{v}}_{max},|\ddot{\mathbf{x}(t)}|\le {\mathbf{a}}_{max},|\stackrel{...}{\mathbf{x}(t)}|\le {\mathbf{j}}_{max}\text{\hspace{1em}(15)}$$

앞서 다항식으로 생성한 궤적에 대해 미분하여 위 수식을 풀어내어 constraints 충족 여부를 따져볼 수 있다.

2) Collision Free Primitives 선행 연구들에서는 장애물의 크기를 더 크게 하여 보수적으로 고려하고, 기체를 구나 각기둥으로 고려하였다.

본 논문에서는 반지름 $r$ 과 높이 $h$ 를 가지는 타원체(ellipsoid) $\mathcal{E}\in {\mathbb{R}}^3$ 로 고려하였다. 그리고 pointcloud로 만들어진 장애물들을 $O\subset {\mathbb{R}}^3$ 로 정의하였다.

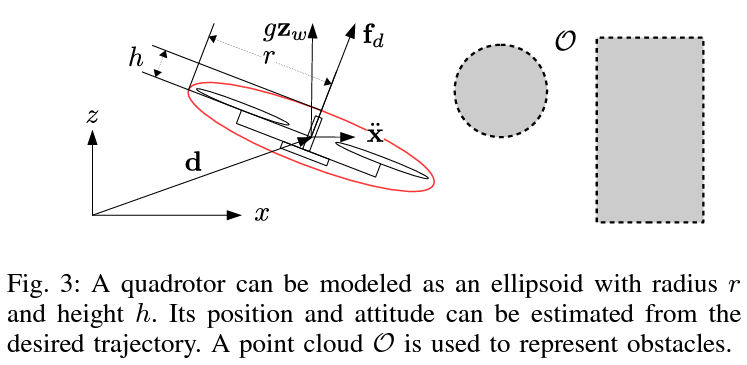
따라서, 주어진 기체의 state $\mathbf{s}$ 에서의 body configuration(타원체의 상태)는 아래와 같다.

$$\mathcal{E}(s):=\{p=E\tilde{p}+d|\Vert \tilde{p}\Vert \le 1\}\text{\hspace{1em}(17)}$$

where

$$d=\mathbf{x}(t),E=R\left[\begin{array}{ccc}r& 0& 0\\ 0& r& 0\\ 0& 0& r\end{array}\right]R^T\text{\hspace{1em}(18)}$$

Todo

• Lie theory와 SE(3), SO(3)

Question

• 수식 (17, 18) 의미 이해 ($d=x(t)=p$가 아닌지?)

Solved (23.11.21)

동일한 것은 맞으나 시간에 따라 달라지는 state를 $d$ 로 정의한 것이고, $E\tilde{p}$ 를 통해 결국 CoM으로부터 타원체 안에 있는 모든 점들을 의미한다.

Note

• 타원체보다 정확하게 4개의 타원과 구로 이루어진 configuration은 어떨까
• 3x3 크기의 행렬에서 표현이 어려울 것으로 보임

orientation $R$ 은 $\ddot{\mathbf{x}}(t)$와 중력 가속도 $g$ 로부터 얻을 수 있다. 자세한 내용은 quadrotor dynamics 참고

이를 가지고 기체와 장애물의 충돌 여부를 경로에서의 타원체 영역과 장애물 간의 교점이 생기는지로 판단할 수 있다.

$$\mathcal{O}\cap \mathcal{E}=\{o|\Vert E^{-1}(o-d)\Vert \le 1,\forall o\in \mathcal{O}\}=\varnothing \text{\hspace{1em}(19)}$$

본 논문에서는 모든 pointcloud에 대해 확인하는 대신 KD-tree를 이용하여 부분집합 ${\mathcal{O}}_{r,d}$ 에 대해 고려하였다. 이 부분집합은 $d$ 에서의 반지름 $r$ 안에 있는 pointcloud 이다. ($\because r\ge h$)

Note

• KD-tree 보다 효율적인 pointcloud 구조체
• 혹은 다른 형태의 body configuration을 통한 subset 재정의

문제는 타원체가 그리는 궤적(contour of an ellipsoid)는 convex하지 않으므로 a primitive $F_n$ 에서 $I$ 만큼의 state만 고려하여 collision-free 를 판단한다.

이러한 feasibility constraints $F_n(t)\subset {\mathcal{X}}^{free}$ 를 정리하면 아래와 같다.

$$\begin{array}{rl}{F}_n(t)& \le [{\mathbf{v}}_{max}^T,{\mathbf{a}}_{max}^T,{\mathbf{j}}_{max}^T]\\ \mathcal{O}\cap \mathcal{E}(s_{i,n})& =\varnothing ,\forall i=\{0,1,\dots ,I\}\end{array}\text{\hspace{1em}(21)}$$

이 때 $s_{i,n}$ 은 $F_n$ 에서 고려한 $0,\dots ,I$ 에서 $i$ 번째로 선택된 state 이다.

Trajectory Refinement

경로 생성의 smoothness를 위해서 $C^2$ continuity가 필요하다. 이는 Continuous Second Derivative 로 궤적에서의 가속도도 연속적이어야 함을 의미한다. 따라서 jerk를 control input으로 사용해야 하고 state space는 위치, 속도, 가속도로 이루어지므로 ${\mathbb{R}}^9$ 에 해당한다.

이러한 고차원의 공간에서의 경로계획은 시간과 메모리 소요가 크다. 본 논문에서는 lower dimensional space에서 만들어진 경로를 가이드삼아 higher dimensional space에서 경로를 만드는 hierarchical 방식을 제안한다.

A. Trajectories Planned in Different Control Spaces

속도, 가속도, jerk를 각각 control input으로 삼는 궤적을 ${\Phi }^j,j=1,2,3$라고 한다. 이 때 최적의 경로에 소요된 control effort $J^j$를 아래와 같이 정의한다.

$$J^j={\int }_0^J\Vert {\mathbf{x}}^{(j)}{\Vert }^{2}dt\text{\hspace{1em}(22)}$$

본 논문에서 실험을 통해 $j$ 가 증가함에 따라 실행 시간 $T^j$ 와 연산 시간 $t^j$ 는 증가함을 알 수 있다.

• $T^1<T^2<T^3$
• $t^1<t^2<t^3$

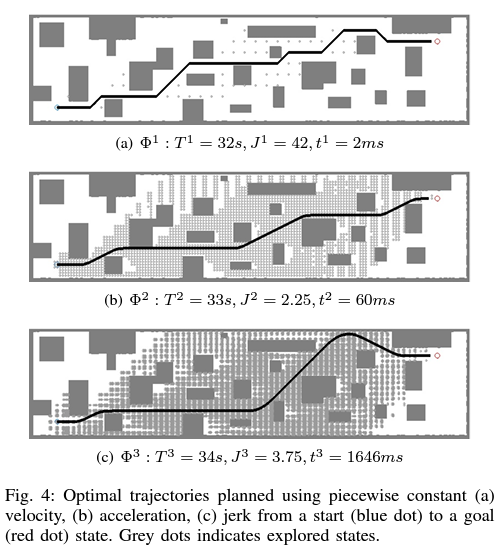
control input의 차원이 하나씩 커질 수록 연산 시간은 대략 20~30배 증가한다.

B. Using Trajectories as Heuristics

이전에 얻은 저차원 공간에서의 궤적을 ${\Phi }^p$, 탐색하려는 고차원 공간에서의 궤적을 ${\Phi }^q(q>p)$ 라고 한다.

${\Phi }^q$ 에서 각 primitive 간의 시간 간격은 $\tau$ 라고 가정하고, 그래프에서의 각 격자(lattice) $s_n^q$ 는 시작부터 현재 격자까지 걸린 최소시간 $T_n$ 과 연관되어 있다고 가정한다. 따라서 $T_n$ 은 $\tau$ 의 정수배이다.

선행 논문 [3]에서는 heuristic $H(s_n^q)$ 를 현재 state $s_n^q$ 에서부터 목적 $s_g$ 까지 계산했지만 본 논문에서는 이전에 얻은 ${\Phi }^p$ 와 $T_n$ 을 통해 구한 중간 지점(intermediate goal) $s_n^p={\Phi }^p(T_n)$ 을 이용한 heuristic을 제안한다.

$$H(s_n^q,{\Phi }^p)=H_1(s_n^q,s_n^p)+H_2(s_n^p,s_g)\text{\hspace{1em}(23)}$$

$H_1(\cdot )$ 은 Appendix에 정리되어 있으나 여기서 정리해보도록 한다.

---

Appendix: Linear Quadratic Minimum Time for Jerk Control

그래프 탐색에서의 heuristic function $H(s,s_g)$ 는 constraints를 완화하여 얻은 실제 cost의 underestimation 이다. underestimation의 의미는 아래와 같이 설명할 수 있다.

• 만약 heuristic이 실제 cost를 정확히 예측하면, 경로 탐색은 가장 효율적이라고 할 수 있다.
• 만약 heuristic이 cost를 underestimation한다면, 탐색 알고리즘은 여전히 최적 경로를 찾을 수 있지만, 필요한 것보다 더 많은 노드를 탐색할 수 있다.
• 만약 heuristic이 비용을 overestimation한다면, 탐색된 경로는 최적이 아닐 수 있으며, 이는 suboptima 일 수 있다.

Problem 2의 cost인 heuristic $H$ 를 풀어 state $s$ 와 $s_g$ 사이의 최적 경로를 찾고자 한다. 위치, 속도, 가속도에 대해서는 선행 연구[3]에서 보였고 여기에서는 jerk control에 대해 보인다.

Problem 2 주어진 현재 state $s$, 목적 state $s_g$ 에 대해 아래와 같은 cost function을 갖는 최적 경로를 찾는다.

$$c\underset{\mathbf{j},T}{\min }{\int }_0^T\Vert \mathbf{j}{\Vert }^{2}dt+\rho T\text{\hspace{1em}(28)}$$

초기 state $s=[p_0^T,v_0^T,a_0^T{]}^T$ 라고 가정하면 Pontryagin’s minimum principle에 의해 아래와 같이 최적 경로의 위치 수식이 정리된다.

$$p=\frac{d_5}{120}{t}^5+\frac{d_4}{24}{t}^4+\frac{d_3}{6}{t}^3+\frac{a_0}{2}{t}^2+v_{0}t+p_0\text{\hspace{1em}(29)}$$

계수 $d_i,i=3,4,5$는 논문 [4]에서 $s,s_g,T$ 를 통해 정의되었다.

따라서 식 (28) 에서 cost function $C(T)$ 를 정리하면 아래와 같다.

$$\begin{array}{rl}C(T)& ={\int }_0^T(\frac{d_5}{2}{t}^2+d_{4}t+d_3{)}^{2}dt+\rho T\\ & =\frac{d_5^2}{20}{T}^5+\frac{d_4^T{d}_5}{4}{T}^4+(\frac{d_4^T{d}_4}{3}+\frac{d_3^T{d}_5}{3})T^3+d_3^T{d}_4{T}^2+d_3^{2}T+\rho T\end{array}\text{\hspace{1em}(30)}$$

즉 위의 $p(t)$ 를 3번 미분하여 $j(t)$ 를 얻어 Problem 2 의 cost 부분에 넣어 계산한 것이다.

$C(T)$ 의 최솟값은 $T$ 에 대해 미분하여 해 $T^{\ast }$ 를 찾음으로써 구할 수 있다.

$$\frac{dC}{dT}=c_0+\cdots +c_6{T}^{-6}=0,T\in [0,\infty )\text{\hspace{1em}(31)}$$

계수 $c_i,i=0,\dots ,6$ 들은 앞서 초기 state $s$ 와 목적 state $s_g$ 를 통해 아래와 같이 결정된다.

결국, $H(s,s_g)=C(T^{\ast })$ 이다.

---

다시 수식 (23)으로 돌아가 살펴보자.

$H_1(\cdot )$ 은 현재 state $s_n^q$ 로부터 중간 목표 지점 $s_n^p$ 까지의 최적 경로이다. $H_2(\cdot )$ 는 ${\Phi }^p$ 를 통해 아래와 같이 정리할 수 있다.

$$H_2(s_n^p,s_g)=J^q(s_p^n,s_g)+\rho (T^p-T_n)\text{\hspace{1em}(24)}$$

여기서 $T^p$ 는 이전에 얻은 저차원 궤적 ${\Phi }^p$ 의 실행 시간이다. 그리고 $J^q(s_p^n,s_g)$ 는 이 경로를 따라 $s_n^p$ 로부터 $s_g$ 까지 소요된 control effort 수식 (22) 이다. $J^q$ 인 이유는 여기서의 control input의 dimension이 $p$ 가 아닌 $q$ 이기 때문이다.

하지만 저차원 궤적 ${\Phi }^p$ 에서는 $\mathbf{x}$ 의 $q$ 차 미분값을 사용하지 않으므로 $J^q(s_p^n,s_g)=0$ 이 된다.

다시 식 (24)를 정리하면 아래와 같다.

$$H_2(s_n^p,s_g)=\rho (T^p-T_n)\text{\hspace{1em}(25)}$$

하지만 마지막에 저자는

“the heuristic function defined in (23) is not admissible since it may not necessarily be the under-estimation of the actual cost-to-goal”

이라고 언급하였다. (??)

그럼에도 Fig. 4.에서 수행한 경로 계획을 수식 (23)을 적용하면 아래와 같이 control effort와 실행 시간은 커지지만 연산 시간과 그래프 탐색에 고려된 노드의 숫자가 훨씬 적음을 아래 그림으로 보였다.

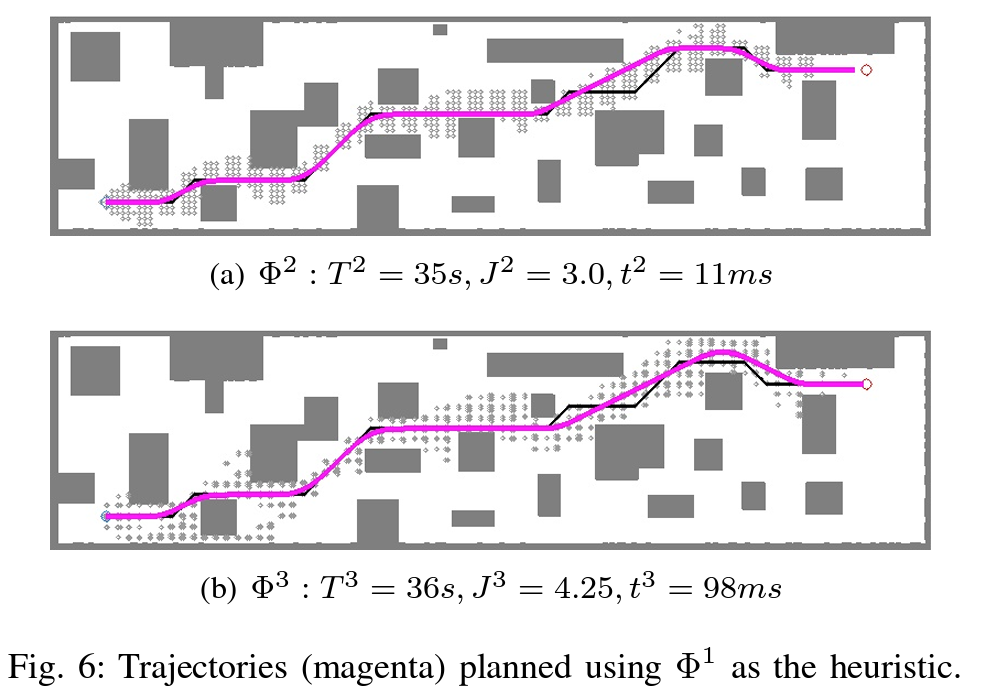
Evaluation과 Experiments 는 생략하였다. 끄읏

Question

• : Collision Free Primitives 부분
• 일정 $I$ states 까지 충돌 여부를 확인하는데 이 때의 $I$ 는 어떻게 선택하는가? $t\in [0,\tau ]$ 에서도 일부 취하는 것으로 보인다.. 그렇다면 미리 주어진 장애물 지도가 있어야 하는 것인지 혹은 주어진 센서 범위 안에서만 수행하는 것인지?
• : 수식 (23) ~ (25) 부분.
• Appendix와 식 (23)을 이해했을 때는 같은 $n$ 번째 lattice 에 도달하는데 걸린 $T_n$ 은 $p$ 와 $q$ 에서 다른 값이 된다. 현재까지의 궤적 ${\Phi }_n^q$ 에서 $s_n^q={\Phi }_n^q(T_n)$ 이고, $s_n^p={\Phi }^p(T_n)$ 이라고 할 때, $s_n^p$ 이 왜 undefined states 인지는 모르겠으나..
• $H_1(\cdot )$ 은 이 둘 간의 궤적을 구하고, $H_2(\cdot )$ 은 이전에 구한 저차원 궤적으로 남은 부분을 취하는 것으로 이해하였다.
• 그러면 본 논문에서 사용한 heuristic $H$ 는 jerk control을 사용하되 저차원 궤적을 따라가도록 만들어진 함수로 봐도 되는 것일까?

Solved (23.11.21)

• 이전 논문에서는 map resolution을 바탕으로 선택하였지만 본 논문에서는 튜닝 가능한 영역으로 보임. Fig.2 에서도 elements에 대한 내용이 있고 Yang et al.에서도 control effort 의 range, step에 tuning이 필요한 것을 문제로 지적함.
• $A^{\ast }$ 알고리즘과 거의 동일하다고 생각해야 한다. 이전 궤적 ${\Phi }_n^p$ 을 구하는 것이 아니라 처음부터 목적 지점까지 탐색해가면서 경로를 계획할 때, 중간 지점에서는 그 때의 state 까지 고차원에서의 cost를 계산하고 목적 지점까지는 그냥 최단시간 경로로 계획하는 것을 $H_1+H_2$ 로 표현한 것이다.