[ICRA '21] Whole-Body Real-Time Motion Planning for Multicopters

Whole-Body Real-Time Motion Planning for Multicopters

S. Yang, B. He, Z. Wang, C. Xu and F. Gao, “Whole-Body Real-Time Motion Planning for Multicopters,” 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 2021, pp. 9197-9203, doi: 10.1109/ICRA48506.2021.9561526.

PDF / Publisher Link

앞선 Sikang. et al. 이후로 나온 Motion Planning 논문으로 실험에서 직접 비교하며 여러 문제점을 지적하였다.

Sikang 논문에서 문제로 지적한 (dynamics 고려없는) $A^{\ast }$ 로 경로 생성 이후에 optimazation 하는 방식이며 Results에서 궁금한 부분도 있었지만 연산 속도와 메모리 소요를 매우 크게 줄였다.

다만, Sikang 논문보다 수식에서의 설명이 추상화되어있고 코드도 명확하게 공개하지 않아 이해하기 어려웠다.

주요 Contributions

• 다면체(polyhedron)를 통해 3차원 공간에서의 연산이나 OCP의 constraints를 해결
• 타원체 대신 직육면체(tilted cuboid)로 기체 모델링
• Dynamically feasible, collision-free한 OCP를 unconstrained optimization으로 해결
• 이를 위해 nonlinear constraints 들은 cubic penalty function을 사용함

A milliseconds-level full-body optimazation-based trajectory planning with collision-free and dynamic feasibility

Introduction

Quadrotor가 비행을 하며 그리는 궤적이 non-convex 하기 때문에 dynamics와 collision-free를 모두 고려하여 real-time으로 OCP를 푸는 것은 어려운 문제이다.

그래서 non-convex constraints를 가진 최적화 문제에서는 여러 feasible regions을 가지고 이에 여러 local minima에 빠지게 된다.

당시 연구들은 대부분 장애물을 가장 긴 길이만큼 확장하여 드론의 방향을 무시하고 free space를 완전히 활용하지 못하였다.

Question

• 위 내용에서 드론의 방향을 무시한다는 것이 어떤 의미인지? 말그래도 yaw 값이 무시되었다는 건가?
• 장애물을 긴 방향을 확장한다는 것은 이해하였으나 이 과정에서 드론의 방향을 무시한다는 것은 어떤 관련이 있는지 이해하지 못함.
• 아래는 논문 내용, 이후에 이어지는 내용으로 attitude 이야기 일 수도 있으나 일단은 orientation으로 표현함.
• The mainstream work-around is to ignore the orientation of drones completely by dilating obstacles radically according to its largest axis length, which leads to conservative performance that does not fully exploit free spaces.

드론의 자세(attitude)를 고려하는 당시의 optimization-based 방법들은 고차원의 다양체에서(manifolds residing in high dimensions) 문제를 정의하거나 환경에 대한 가정을 사용하고 있었다.

search-based 방법이나 discretized space를 통해 최적화 문제를 푸는 방법들은 많은 연산 시간과 높은 메모리 사용이 필요하지만 때때로 좋지 않은 결과를 내었다.(아마도 discretization에서의 문제)

본 논문은 일련의 다면체로 3차원 공간을 표현하여 dynamically feasible한 경로를 만드는 자신들의 선행 연구를 기반으로 드론의 자세를 명확히 구해내 이를 constraints 대신 목적 함수의 penalty term으로 넘겨 OCP를 풀어낸다.

Previous work

• Z. Wang, X. Zhou, C. Xu, and F. Gao, “Geometrically constrained trajectory optimization for multicopters,” arXiv preprint arXiv:2103.00190, 2021.

추후 T-RO로 나온다…

Related Work

참고할 논문 / 고려할 만한 선행 연구, 언급 위주로만 정리

본 논문이 ZJU-FAST-Lab 연구실에서 나왔고, HKUST Aerial Robotics Group, MaRS 랩과 더불어 드론의 자율비행 관련 연구를 많이 진행한 곳이다.

convex polyhedrons 로 free space를 표현하고, Safe flight corridors 개념으로 확장하여 비행과 연결지은 연구들도 여기 저자들이 많이 작성하였고, 본 논문에도 해당 개념이 적용되었다. (추후의 T-RO 논문도 해당 내용이 들어간다.)

Free spaces with polyhedrons

3. F. Gao, L. Wang, B. Zhou, X. Zhou, J. Pan, and S. Shen, “Teach-repeat-replan: A complete and robust system for aggressive flight in complex environments,” IEEE Transactions on Robotics, 2020.
4. X. Zhong, Y. Wu, D. Wang, Q. Wang, C. Xu, and F. Gao, “Generating large convex polytopes directly on point clouds,” arXiv preprint arXiv:2010.08744, 2020.
5. S. Liu, M. Watterson, K. Mohta, K. Sun, S. Bhattacharya, C. J. Taylor, and V. Kumar, “Planning dynamically feasible trajectories for quadrotors using safe flight corridors in 3-d complex environments,” IEEE Robotics and Automation Letters, vol. 2, no. 3, pp. 1688–1695, 2017.

Optimization-based 방식으로 aggressive한 (=high-dimension) 경로 계획을 하는 연구들도 제시되었다.

Single gap crossing with optimization-based methods

9. G. Loianno, C. Brunner, G. McGrath, and V. Kumar, “Estimation, control, and planning for aggressive flight with a small quadrotor with a single camera and imu,” IEEE Robotics and Automation Letters, vol. 2, no. 2, pp. 404–411, 2016.
10. D. Falanga, E. Mueggler, M. Faessler, and D. Scaramuzza, “Aggres-sive quadrotor flight through narrow gaps with onboard sensing andcomputing using active vision,” in 2017 IEEE international conference on robotics and automation (ICRA). IEEE, 2017, pp. 5774–5781.
11. J. Lin, L. Wang, F. Gao, S. Shen, and F. Zhang, “Flying through a narrow gap using neural network: an end-to-end planning and control approach,” arXiv preprint arXiv:1903.09088, 2019.

위 연구들은 좁은 틈을 지나는 것에 초점을 맞추었고 전반적인 경로 계획은 크게 고려되지 않았다. 그래서 geometrical constraints에 대한 가정이 전제되었다.

Trajectory optimization algorithm 선행 연구로는 아래 논문이 있는데, 다양체(manifold)에서 경로 계획이 이루어 졌고, resource(e.g. memory or computation time)에 대한 측정이나 비교가 없다.

Manifold trajectory optimization

12. M. Watterson, S. Liu, K. Sun, T. Smith, and V. Kumar, “Trajectory optimization on manifolds with applications to quadrotor systems,” The International Journal of Robotics Research, vol. 39, no. 2-3, pp. 303–320, 2020.

Todo

• Manifold
• a parameterization invariant manifold / manifolds are parameter-heavy

마지막으로 search-based 방식의 motion planning인 Liu et al. 의 문제점을 지적하였다.

1. Motion primitives를 만들어 낼 때 불필요한 탐색이 많이 일어난다.
2. control input의 범위와 step에 튜닝이 필요하다.
3. 고정된 control resolution으로 인해 유연한 경로 생성이 어렵다.

결과 비교를 하면서 더 많이 지적한다.

Preliminaries

A. Generation of Body Attitude from Differential Flatness

드론의 differential flatness를 이용해 표현되는 orientation $R_b$ 에 대한 설명으로 디테일함은 생략하고 수식 위주로 작성하였다.

Todo

• Orientation of quadrotor dynamics
• 확실히 정리하고 가기 + quaternion 표현으로도

B. Geometrically Constrained Trajectory Optimization for Multicopters Framework Revisit

1) Optimality Condition for Unconstrained Problem

주어진 $t_0<t_1<\cdots <t_M$ 의 time duration $[t_0,t_M]$ 에 대해 선행 논문에서 제시된 multi-segment minimum control effort problem for a chain of s-integrators는 아래와 같다.

$$\begin{array}{rl}\underset{p(t)}{\min }& {\int }_{t_0}^{t_M}u(t{)}^{T}Wu(t)dt\\ s.t.& u(t)=p^{(s)}(t),\forall t\in [t_0,t_M]\\ & p^{[s-1]}(t_0)=\overline{p_o},p^{[s-1]}(t_M)=\overline{p_f}\\ & p^{[d_i-1]}(t_i)=\overline{p_i},1\le i<M\end{array}\text{\hspace{1em}(5a)(5b)(5c)(5d)}$$

$p(t):[t_0,t_M]\to {\mathbb{R}}^m$ 은 flat output이고, $u$ 는 $p$ 의 s번째 미분으로 control input으로 작용된다. (Liu et al. 과 동일)

$p^{[s-1]}=[p^T,{\dot{p}}^T,\dots ,(p^{(s-1)}{)}^T{]}^T\in {\mathbb{R}}^{ms}$ 로 $s-1$ 차 까지의 미분값들 (i.e. 위치, 속도, 가속도, …)의 initial, final conditions 이며 $p^{[d_i-1]}\in {\mathbb{R}}^{m{d}_i}$ 는 중간 timestamp $t_i$ 에서의 $d_i-1\forall (d_i-1)<s$ 차 까지의 미분값들 이다.

Theorem 2 (Optimality Condition) in Prev. work

이해한 바로는 Liu et al.의 식 (8) 과 결론적으로 같은 내용이다. 계수와 time $t$ 로 이루어진 다항식 $p(t)$ 는 $\overline{d_i}-1$ 차 까지 연속이고 미분 가능하다. $\overline{d_i}-1=(2s-d_i)-1$

Question

• $d_i$ 의 정의가 따로 나와있지 않은데(못찾았거나), 어떤 $d_i$ 에 대해로 해석하면 되나?
• 왜 주어진 중간값의 차수가 $d_i$ 일 때 $\overline{d_i}+d_i=2s$ 인지

Solved ?

• 일단 $N=2s-1$ 은 boundary condition으로 연결된 다항식 차수이다. initial, final condition이 0 ~ $s-1$ 차까지 $2s$ 개의 계수가 필요하고 이는 $2s-1$ 차 다항식이어야 한다.
• $d_i$ 는 $i$ 개로 조각낸 다항식 $p_i(t)$ 과 연관이 있어보인다. intermediate timestamp $t_i$ 에서 $d_i$ 개의 condition이 더 있으므로 $\overline{d_i}$ 차까지의 연속, 미분 조건이 필요한 것으로 보인다. (overconstrained 하지 않기 위해)

그래서 전체 계수 벡터와 주어진 초기, 중간, 최종 다항식($q,T$)을 합쳐 수식 (9)로 정리($M$ - 단계의 $c$로 변수화된 경로)되었다.

여기서는 최적의 중간 지점 $q^{\ast }$ 와 time allocation $T^{\ast }$ 를 찾는 것에 초점을 맞춘다고 한다.

$$\begin{array}{rl}\underset{q,T}{\min }& H(q,T)\\ s.t.& \text{certain constraints}\end{array}\text{\hspace{1em}(10a)(10b)}$$

여기서부터 점점 무슨 소리인지 이해를 못하였다… $H(q,T):=F(c(q,T),T)$ 인데 $F(c,T)$ 는 user-defined control effort of a piecewise polynomial 이라고 한다. 아마도, $[t_{i-1},t_i)$ 에서의 다항식 $p_i(t-t_{i-1})$ 의 $s$ 차 미분값을 의미하는 것으로 보인다.

선행 연구에서는 주어진 $\frac{\partial F}{\partial q},\frac{\partial F}{\partial c}$ 에 대해 $\frac{\partial H}{\partial q},\frac{\partial H}{\partial T}$ 가 $O(M)$ 의 시간, 공간 복잡도로 얻어질 수 있다는 것을 보였다고 한다.

Question

• 왜 $\frac{\partial F}{\partial c},\frac{\partial F}{\partial T}$ 가 아니라 $\frac{\partial F}{\partial q},\frac{\partial F}{\partial c}$ 인지?

2) Geometrically Constrained Optimization

앞에서의 multi-segment control effort 를 포함하여 전체적인 OCP는 아래와 같이 정의된다. 마찬가지로 Liu et al.에서의 문제와 동일하다.

$$\begin{array}{rl}\underset{p(t),T}{\min }& {\int }_0^{T}u(t{)}^{T}Wu(t)dt+\rho (T)\\ s.t.& u(t)=p^{(s)}(t),\forall t\in [0,T]\\ & \mathcal{G}(p(t),\dots ,p^{(s)}(t))⪯0,\forall t\in [0,T]\\ & p(t)\in \mathcal{F},\forall t\in [0,T]\\ & p^{[s-1]}(t_0)=\overline{p_o},p^{[s-1]}(T)=\overline{p_f}\end{array}\text{\hspace{1em}(11a)(11b)(11c)(11d)(11e)}$$

익숙한 OCP 듯이, $\mathcal{F}$ 는 obstacle-free region 이고, $\mathcal{G}$ 는 nonlinear inequalities 이다. 본 논문에서는 어떤 식으로 이 두 가지 constraints를 풀어내는지 보자.

우선 마찬가지로 yaw를 고려하지 않는다.(i.e $\psi =0$)

obstacle-free region(=flight corridor) 는 $M$ 개의 polyhedrons의 $\mathcal{H}$ -representation 으로 근사하여 표현된다. 그리고 이 polyhedrons들은 서로 교집합이 생기도록 연속되어 구성되어 있다. 이를 수식으로 표현하면 아래와 같다.

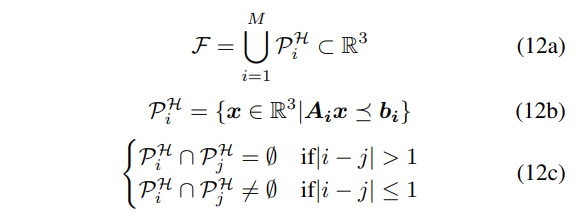
$A_{i}x\le b_i$ 는 polyhedron 을 수학적으로 표현한 것이다. (convex optimization 참고)

그리고 (12c)는 결국 연속된 index 끼리는 겹치는 구역이 생긴다는 의미이다.(i.e. consecutively intersected)

B. 1)에서 optimality condition에 대한 추론을 활용하여 식 (11)을 식 (10)과 같은 구조로 표현하면 아래와 같다.

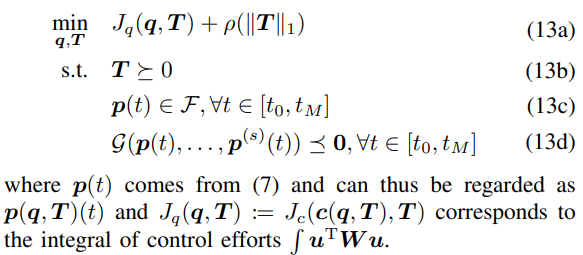
Question

• $u(t)=p^{(s)}(t)$ 조건은 자연스레 내재된걸로 하는 건가? ⇒ 그런듯!

본 논문은 diffeomorphism based method를 통해 수식 (13)의 constraints를 제거하고 quasi-Newton method로 풀어낸다.

Todo

• diffeomorphism based method

자세한 내용은 이미지 참고. 중요한 내용들은 다음 챕터에 나온다. 그리고 앞 논문을 보아야 조금 더 자세히 이해 될 것 같다.

Full-body Motion Planning

드론 기체의 모델링과 full-body collision-free 조건을 어떤 식으로 풀어 냈는지 살펴보자.

A. Quadrotor Modeling and Trajectory within Polyhedrons

참고

M closed convex polyhedrons를 아래와 같이 표현할 수 있다.

$${\mathcal{P}}_i^{\mathcal{H}}=\{q\in {\mathbb{R}}^3|(n_i^k{)}^T(q-o_i^k)\le 0,k=1,\dots ,K_i\},\forall i\in \{1,2,\dots ,M\}\text{\hspace{1em}(14)}$$

처음에는 이해를 못했는데, hyperplane 들로 둘러싸여 만들어진 polyhedron 그림을 떠올려서 이해했다. (convex optimization 참고)

각각의 hyperplane의 법선 벡터 $n_i^k$ 와의 내적이 음수인 점 $q$ 의 집합, 그리고 그 집합들 간의 교집합.

그리고 3차원 공간의 점 $q$ 는 드론의 모델링 공간 안에 있는 점이다. 이전 논문에서는 타원체로 하여 표현하였다. 디테일한 내용은 아래 이미지로 대체.

본 논문은 타원체 대신 직육면체로 표현하였다. 이렇게 한 이유는 훨씬 단순함도 있지만, CoM이 반드시 드론 부피의 중심점이 아닐 수 있기 때문이다. 폭으로는 fixed 전제이므로 중앙이겠지만, 높이 상으로는 아닐 수 있고 이렇게 되면 타원체 하나로 표현할 수 없기도 하다.

(Liu et al. 에서 명확하게 설명을 안하기도 했고, 단순히 body frame 기준 프롭 거리, 높이로 하면 프로펠러 끝 지점이 충돌할 수 있다.)

따라서 ${\mathcal{Q}}_i(t)$ 는 $i$ 번째 궤적을 드론 모델대로 확장한 (=직육면체의 연속적인 궤적) 이다.

수식으로 표현해보면,

$$\begin{array}{r}{\mathcal{G}}_{att}^v(p_i(t),{\ddot{p}}_i(t)=A_i(p_i(t)+R_b^i(t){\tilde{q}}_v)-b_i\in {\mathbb{R}}^{K_i})\\ {\mathcal{G}}_{att}(p_i(t),{\ddot{p}}_i(t)=[[{\mathcal{G}}_{att}^v(p_i(t),{\ddot{p}}_i(t{)}^T{]}_{v=1}^8{]}^T\end{array}\text{\hspace{1em}(19a)(19b)}$$

Body attitude를 참고하면 $R_b^i$ 에 의해 ${\mathcal{G}}_{att}$ 의 인자가 $p_i,{\ddot{p}}_i$ 인 것을 볼 수 있고 이는 다항식으로 이루어져 ${\mathcal{G}}_{att}(c_i,T_i)$ 로 표현 가능하다. (i.e. ${\mathcal{Q}}_i(t)\subset {\mathcal{P}}_i^{\mathcal{H}},\forall t\in [0,T_i]$)

하지만 논문에서 언급된 대로 두 polyhedron 교차 지점 안에 드론 궤적을 모델대로 확장한 것이 그대로 들어가지는 않는다.

the inflated drone trajectory does not necessarily stay within either the intersection of two polyhedrons

정밀하게 풀어내는 방법은 mixed-integer optimization 인데 이는 online computation에서 너무 시간이 많이 소요된다고 한다. 그리고 실험에서 보았을 때 큰 영향이 없다고 한다.

Question

• 왜 mixed-integer optimization으로는 제대로 풀어낼 수 있는건가?

B. Construction of Constraint Violation Function

제일 이해하기 어려웠던 파트.

이전 챕터에서 제시된 ${\mathcal{G}}_{att}$ 는 비선형 조건으로 바로 풀어내기 어려워 본 논문에서는 조건을 위반할 수 있는 잠재성을 고려한다고 한다.

only consider the potential violation happens at normalized timestamps and construct the constraint violation function $G_{att}$ at the normalized timestamp $\hat{i}$

$$\begin{array}{rl}{G}_{att}^k(c_i,T_i,\hat{t})=[(n_i^k{)}^T(p_i(\hat{t}\cdot T_i)& +R_b^i(\hat{t}\cdot T_i){\tilde{q}}_v-o_i^k){]}_{v=1}^8\in {\mathbb{R}}^8\\ G_{att}(c_i,T_i,\hat{t})& =[[G_{att}^k(c_i,T_i,\hat{t}{)}^T{]}_{k=1}^{K_i}{]}^T\end{array}\text{\hspace{1em}(20a)(20b)}$$

$G_{att}:{\mathbb{R}}^{2s\times 3}\times {\mathbb{R}}_{+}\times [0,1]\to {\mathbb{R}}^{8K_i}$ 로 정의되는데 dimension이 잘 이해되지 않았다. Theorem 2에서 flat output $m=3$ 이고 각 $2s$ 의 다항식 계수들이 있으므로 ${\mathbb{R}}^{2s\times m}$ 의 다항식 계수 행렬로 이해했다. 이어지는 양의 실수와 정규화된 시간의 공간으로 이해했는데 각각만 이해하고 전체적인 의미를 온전히 이해하지는 못한 것 같다.

Question

• $G_{att}:{\mathbb{R}}^{2s\times 3}\times {\mathbb{R}}_{+}\times [0,1]$

Solved

• 생각해보니 함수에서 $\to$ 의 의미는 정의역에서 치역으로의 의미이므로, 위 공간에 대한 정의는 함수에 들어가는 각각 인자에 해당하는 것이다.
• 따라서 $c_i\in {\mathbb{R}}^{2s\times 3},T_i\in {\mathbb{R}}_{+},\hat{i}\in [0,1]$ 와 같이 정리하면 된다.

그리고 주어진 가중치 벡터 $\mathcal{X}\in {\mathbb{R}}^{8{\mathcal{K}}_i}$ 에 대해 $p_i(t)$ 에서의 time integral penalty function $I_{att}:{\mathbb{R}}^{2s\times 3}\times {\mathbb{R}}_{+}\times {\mathbb{Z}}_{\ge }\to {\mathbb{R}}_{+}$ 을 제안하였다.

$$I_{att}(c_i,T_i,{\kappa }_i)=\frac{T_i}{{\kappa }_i}\sum _{j=1}^{k_i}{w}_j{\mathcal{X}}^{\mathcal{T}}\max [{\mathcal{G}}_{att}(c_i,{\mathcal{T}}_i,\frac{j}{{\kappa }_i}),0{]}^3$$

여기서 $\max [\cdot ,0{]}^3$ 은 entry-wise maximum and entry-wise cubic function의 합성 함수이다. 그리고 주어진 $\frac{1}{\kappa }$ 는 구적법(quadrature)의 상대적 resolution 이고 $w_j$ 는 $j$ 번째 구적법 계수이다.

• entry-wise cubic function $f(x)$: 벡터 $\mathbf{x}=[x_1,\dots ,x_n]$ 에 대해 각 요소에 세제곱 하는 함수로 $f(\mathbf{x})=[x_1^3,\dots ,x_n^3]$ 이다.

따라서 composite function of entry-wise maximum and cubic 이란 각 요소에 세제곱한 값과 0 중 큰 값을 취하는 함수이다.

(e.g. $g(\mathbf{x},0)=[\max (x_1^3,0),\max (x_2^3,0),\dots ,\max (x_n^3,0)]$)

앞서서 $M$ 개의 경로로 나눴으므로 전체 궤적에 대힌 penalty tern은 아래와 같다.

$$I_{\sum att}(c,T)=\sum _{i=1}^M{I}_{att}(c_i,T_i,{\kappa }_i)\text{\hspace{1em}(22)}$$

이 페널티 함수는 목적 함수에 바로 더해져 수식 (13) 을 unconstrained optmization으로 해결할 수 있게 되었다.

이렇게 Cubic penalty 와 같은 방식의 페널티 함수는 최적화 문제에서 종종 사용된다고 한다. 입력과 목표값간의 차이가 클 수록 페널티가 더 커지게 된다.

Question

• entry-wise cubic & maximum function 은 이해하였으나 구적법 과정에서 relative resolution $1/{\kappa }_i$ 과 구적법 계수 $w_j$ 의 의미
• 이미 weight vector $\mathcal{X}$ 이 있는데 이게 어떤 의미가 있는지?

수식 (14), (19), (20)을 쭉 타고오면서 이해한 내용을 정리해보자. $i\in \{1,2,...,M\},k=1,\dots ,K_i$ 임을 유의한다.

i 번째 궤적에서 $K_i$ 개의 hyperplane으로 둘러쌓여 만들어진 polyhedron 안에 8개의 꼭짓점이 있는지 확인하여 collision-free를 확인한다.

수식(19)와 (20)은 단지 각각의 꼭짓점들이 $K_i$ 개의 hyperplane에서 모두 안전한지 따로 확인(19)하는지와 8개의 꼭짓점을 모든 $K_i$ 개의 hyperplane에서 안전한지 확인(20) 하는 같은 내용이지만 다른 방식의 표현이다.

그리고 hyperplane 안에 있으면 법선 벡터와의 내적값이 음수임으로 안전한 경우 페널티는 0이 되고, 충돌하는 점과의 거리가 멀어질수록(=내적 값이 커질수록?) 페널티 값이 세제곱되어 가해진다.

C. Derivation of Derivatives of Attitude Penalty

앞선 수식 (10) 과 수식 (13) 에서 $F(c,T)$ 와 같이 변수화되어 있는 $I_{att}(c_i,T_i,{\kappa }_i)$ 는 전체 목적 함수에 포함되어 최적화 되어야 하므로, $\frac{\partial I_{att}}{\partial c_i}$ 과 $\frac{\partial I_{att}}{\partial T_i}$ 를 구해야 한다. 구체적인 유도과정에 대해서는 Detailed Derivations of Whole-Body Real-Time Motion Planning for Multicopters 에서 다루었다.

Todo

• 수식 유도과정 읽고 이해

${\mathcal{G}}_{att}^k$ 의 $v$ 번째 요소인 ${\mathcal{G}}_{att}^{k,v}$ 의 미분인 $\frac{\partial {\mathcal{G}}_{att}^{k,v}}{\partial c_i}$ 과 $\frac{\partial {\mathcal{G}}_{att}^{k,v}}{\partial T_i}$ 를 서로 다른 $k,v$ 에 대해 합쳐 $\frac{\partial I_{\sum att}}{\partial c}$ 와 $\frac{\partial I_{\sum att}}{\partial T}$ 를 얻어 최적화 과정에서 사용한다.

D. Unifying the Framework

지금까지의 수식 과정에서 dynamics는 포함되지 않아 dynamic feasibility 가 담보되지 않았다. 본 논문에서는 이러한 constraint도 이전 챕터와 마찬가지로 ${\mathcal{G}}_{dyn},I_{\sum dyn}$ 으로 하여 목적함수에 포함한다.

Question

• 어떻게 dynamics도 polyhedron을 이용해 수식을 구성하였을까

Solved

• 한번 차분히 생각해보자.
• 드론에서는 differential flatness 로 인해 dynamic constraints 는 속도, 가속도 등의 상, 하한으로 정의된다. (e.g. $|v_{max}|\le 4(m/s)$)
• 위의 safety contraints 는 polyhedrone 을 이용하였지만 속도, 가속도는 $p_i(t):=c_i^T{\beta }_0(t)$ 를 미분하여 얻어지므로 $I_{dyn}(c_i,T_i)=\gamma \max [|\dot{p_i}(t)|-v_{max},0{]}^3$ 로 표현 가능하다.
• (물론 resolution 을 사용하면 $\kappa$ 도 마찬가지로 적용되어 integral 해야 한다.)
• 현재속도의 절댓값이 최대 속도의 크기보다 작다면 constraint 를 만족하여 음수가 되므로, penalty = 0 인 것이고 그것이 아니라면(조건을 violate) 한다면 세제곱만큼 커진다.

유한수치해석의 한계(the finite resolution of approximation)로 때때로 비선형 조건 ${\mathcal{G}}_{att},{\mathcal{G}}_{dyn}$ 들이 어겨지는 상황(Violation of nonlinear constraints)이 발생하지만 실험을 통해 전체 경로를 만들어내는 데에는 큰 영향이 없다고 한다.

이제 수식(13)은 완전히 unconstrained optimization problem 이 되어 cddlib과 LBFGS optimizer를 통해 문제를 풀어낸다.

Quote

16. K. Fukuda, “Cddlib reference manual,” Report version 093a, McGill University, Montreal, Quebec, Canada ́ , 2003.
17. K. Fukuda et al., “Frequently asked questions in polyhedral compu-tation.”
18. D. C. Liu and J. Nocedal, “On the limited memory bfgs method for large scale optimization,” Mathematical programming, vol. 45, no. 1-3, pp. 503–528, 1989.

Results

본 논문이 optimization-based full-body motion planning의 첫 연구이므로 앞서 Liu et al. 의 serach-based method를 비교 대상으로하였다. 자세한 내용은 생략하지만 Liu 방식의 문제점들(불필요한 노드 탐색, 2D 경로, 최종 상태의 불안정성)과 연산 속도, 메모리 사용량의 우수함을 보였다.

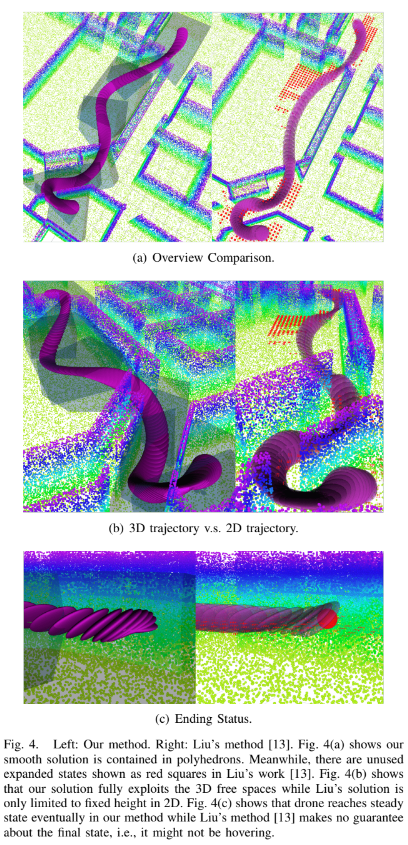
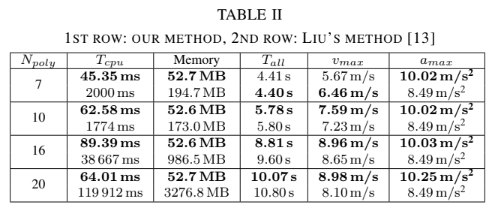
다만 궁금했던 점은, 최적화하기 위한 사전 경로인 $A^{\ast }$ 를 생성하는데 걸린 시간은 포함하지 않았다는 것(Liu는 처음부터 dynamics를 고려하며 그래프 경로 탐색을 수행하므로 불리하다)과 TABLE II 에서 Liu와 본 논문 방식의 polyheron 갯수를 같게 통일했다는 것이다.(같은 시작, 도착점이라도 튜닝해야하는 변수들이 많아 동일한 조건하에서의 경로 계획임이 필요했겠지만…)

정리 끄읏