[RA-L '21] Fast-Racing: An Open-Source Strong Baseline for SE(3) Planning in Autonomous Drone Racing

Fast-Racing: An Open-Source Strong Baseline for SE(3) Planning in Autonomous Drone Racing

Z. Han, Z. Wang, N. Pan, Y. Lin, C. Xu and F. Gao, “Fast-Racing: An Open-Source Strong Baseline for $\mathrm{SE}(3)$ Planning in Autonomous Drone Racing,” in IEEE Robotics and Automation Letters, vol. 6, no. 4, pp. 8631-8638, Oct. 2021, doi: 10.1109/LRA.2021.3113976.

Publisher Link

앞서 ICRA 논문과 경로 생성 방식은 동일하지만 드론 모델링 / GPU 사용 / 시뮬레이션 환경 제안 등을 하며 앞으로의 SE(3) 경로 계획 논문들에 비교할 수 있는 기준을 제시하였다.

nonlinear constraints 를 cubic and max function 으로 바꿔 unconstrained optimization problem 을 quasi-Newton method로 해결하는 내용은 같으나, 다른 방식으로 수식을 표현하여 참고하고 이를 병렬 컴퓨팅으로 연결하여 성능을 개선한 점도 주목할만 하다.

Introduction

드론 레이싱에서 planning 에 대한 벤치마크가 없고 $\mathrm{SE}(3)$ planning 에서 오픈소스로 공개된 baseline도 부재하다.

The reason is that SE(3) planning is much more complicated than traditional planning in ${\mathbb{R}}^3$ because the former requires group operations while conventional optimizers require decision variables in Euclidean spaces.

Todo

• $\mathrm{SE}(3)$ 와 ${\mathbb{R}}^3$ 에서의 planning 차이 명확하게 이해하기

Dataset and AirSim

4. A. Antonini, W. Guerra, V. Murali, T. Sayre-McCord, and S. Kara-man, “The Blackbird Dataset: A large-scale dataset for UAV perception in aggressive flight,” in Proc. Int. Symp. Exp. Robot., Springer, 2018, pp. 130–139.
5. J. Delmerico, T. Cieslewski, H. Rebecq, M. Faessler, and D. Scaramuzza, “Are we ready for autonomous drone racing? The UZH-FPV drone racing dataset,” in Proc. IEEE Int. Conf. Robot. Automat., 2019, pp. 6713–6719.
6. R. Madaan et al., “AirSim drone racing lab,” in Proc. NeurIPS Competition Demonstration, PMLR, 2020, pp. 177–191.

주요 contribution

• simulation platform designed for SE(3) planning
• trajectory optimization based on parallel computing

특히, 다항식과 $max(\cdot ,0{)}^3$ 으로 정리되는 목적함수의 gradient를 total time, constraints point의 discretization number $M,L$ 에 대해 GPU 쓰레드 / 블럭으로 분할하여 연산하는 방식을 제안한 것이 인상적이었다.

문제점

1. a known map / static racing tracks; 좁은 틈은 물론 전체 지도에 대한 정보가 있어야 하고, 동적 장애물에 대한 회피가 불가능하다
2. a global trajectory offline before the racing starts; 처음 최적화를 위한 전역 경로 생성이 필요하다

Related Works

큰 내용이 없어 선행 연구 문제점 짚은 거 정도만 요약

A. Autonomous Drone Racing

드론 레이싱과 같은 환경에서의 visual-based 의 상태 추정(state estimation)을 위한 데이터셋들로 Blackbird dataset[4] 과 UZH-FPV dataset[5] 를 제시하였다.

B. SE(3) Planning

Configuration spaces with neglected attitude of the drone

12. D. Mellinger and V. Kumar, “Minimum snap trajectory generation and control for quadrotors,” in Proc. IEEE Int. Conf. Robot. Automat., 2011, pp. 2520–2525.
14. F. Gao, W. Wu, Y. Lin, and S. Shen, “Online safe trajectory generation for quadrotors using fast marching method and Bernstein basis polynomial,” in Proc. IEEE Int. Conf. Robot. Automat., 2018, pp. 344–351.
15. B. Zhou, F. Gao, L. Wang, C. Liu, and S. Shen, “Robust and efficient quadrotor trajectory generation for fast autonomous flight,” IEEE Robot. Automat. Lett., vol. 4, no. 4, pp. 3529–3536, Oct. 2019.
16. X. Zhou, Z.Wang, H. Ye, C. Xu, and F. Gao, “EGO-Planner: An ESDF-free gradient-based local planner for quadrotors,” IEEE Robot. Automat. Lett., vol. 6, no. 2, pp. 478–485, Apr. 2021.

앞선 논문들에서도 필수적으로 인용되는 [12] 에서는 differentially flat system 과 time vector 와 다항식 계수를 통해 state와 control input을 얻어 내었다.

그러나 위 논문들은 드론의 자세(attitude)가 고려되지 않은 configuration space를 필요로 한다.

아래 논문들은 SE(3) planning 문제를 매우 단순화하여 해결하고, 고정된 attitude constraints 에 대해서만 경로를 계획할 수 있다.

over-simplify SE(3) planning and fixed attitude constraints

17. D. Falanga, E. Mueggler, M. Faessler, and D. Scaramuzza, “Aggressive quadrotor flight through narrow gaps with onboard sensing and computing using active vision,” in Proc. IEEE Int. Conf. Robot. Automat., 2017, pp. 5774–5781.
18. G. Loianno, C. Brunner, G. McGrath, and V. Kumar, “Estimation, control, and planning for aggressive flight with a small quadrotor with a single camera and IMU,” IEEE Robot. Automat. Lett., vol. 2, no. 2, pp. 404–411, Apr. 2017.
19. T. Hirata and M. Kumon, “Optimal path planning method with attitude constraints for quadrotor helicopters,” in Proc. Int. Conf. Adv. Mechatronic Syst., 2014, pp. 377–381.

이제 처음 살펴봤던 Liu et al. 논문이 kinodynamic searching 방식으로 resolution complete한 SE(3) planner를 제안하였으나, search-based method의 한계로 연산 시간이나 메모리 소요가 매우 커서 실제로 사용하기에는 어려움이 있었다.

본인들이 낸 논문인 GCOPTER 가 high-quality 의 SE(3) 궤적을 만들어내었다고 언급하였지만, 이 논문도 적용방식에 대해서 완전히 해결해내지는 못하였다. (병렬 구조를 통한 성능 개선을 위한 언급으로 보임)

GCOPTER

7. Z. Wang, X. Zhou, C. Xu, and F. Gao, “Geometrically constrained trajec- tory optimization for multicopters,” 2021, arXiv:2103.00190.

따라서 본 논문에서는 일반적인 형상의 드론에 적용 가능한 병렬 구조의 최적제어를 실제로 적용하여 baseline으로 커뮤니티에 제공한다.

A High-Performance SE(3) Planner

이전 논문들은 경로 생성(trajectory generation)들 위주로 다뤘다면 본 논문은 경로 계획(trajectory planning)에 더 목적을 맞췄다고 보아야 할 것 같다.

그래서 input 으로는 grid map, initial and goal states 이고 output 으로는 feasible 한 SE(3) 경로를 만들어낸다.

A. Safe Constraint

장애물 회피가 보장된 경로 최적화에 사용될 safe constraint 로 flight corridor를 사용한다.

이 개념은 convex polyhedron 을 사용하여 드론의 모델로부터 주어진 맵과 충돌하지 않는 것을 보장토록 한다.

1. 시작 지점으로부터 경로 탐색을 수행한다.
2. 정해놓은 제한 거리를 넘지 않는 가장 먼 $w_f$ 를 $w_p$ 부터 찾는다. path search 이므로 collision-free 하도록 한다.
3. RILS 를 사용하여 2. 에서 얻은 직선에서 convex polyhedron 을 생성한다.
4. 직선의 중간 지점을 새로운 $w_p$ 로 하여 2. 부터 다시 수행하고 convex hull 안에 마지막 지점이 포함될 때 까지 반복한다.

RILS

21. S. Liu et al., “Planning dynamically feasible trajectories for quadrotors using safe flight corridors in 3-D complex environments,” IEEE Robot. Automat. Lett., vol. 2, no. 3, pp. 1688–1695, Jul. 2017.

Yang et al. 에서 polyhedrons 관련 논문 에서 인용된 논문이기도 하고 연관성 있는 논문도 있어서 나중에 한번 봐도 좋을 것 같다.

B. Problem Formulation

대다수의 내용이 GCOPTER 논문과 Yang et al. 과 유사하다.

드론의 differentially flat system 을 통해 모델링한 vertex ${\hat{v}}^t(t)$ 를 정의하고 이를 polyhedron 으로 정의한다. 그리고 다항식으로 표현할 수 있는 position 을 시간에 대해 분할하여 경로를 수식으로 표현하여 optimal problem을 정의한다.

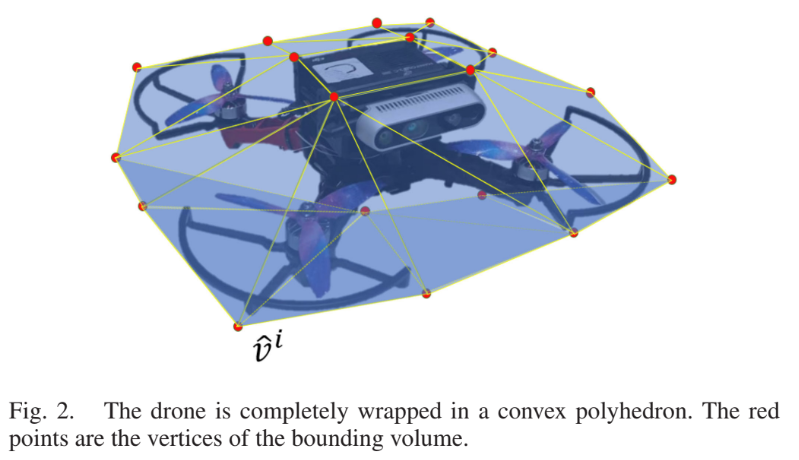
앞서 타원체, 직육면체와 달리 본 논문은 여러 다면체로 표현되는 모델로 정의하였다.

이를 k-DoP (the Boolean intersection of extents along k directions) 혹은 직접 정의하여 아래와 같이 표현한다.

$${\hat{v}}^i(t)=R_b(t)q_v^i+\mathbf{x}(t)\forall i\in \{1,2,\dots ,K\}\text{\hspace{1em}(7)}$$

여기서 $R_b$ 는 드론의 자세를 표현해주는 rotation matrix 이다. $K$ 는 꼭짓접의 수 이고 $q_v^i=[q_{vx}^i,q_{vy}^i,q_{vz}^i{]}^T$ 는 $i$ 번째 꼭짓점의 좌표이다. (당연히 $R_b$ 가 곱해지고 $\mathbf{x}=[p_x,p_y,p_z{]}^T$ 가 더해지므로 body frame 이다.)

polyhedron으로 정의하는 flight corridor 는 아래 이미지로 대체하고 패스…

그래서 constraints 를 고려한 경로 최적화 문제를 아래와 같이 정의한다.

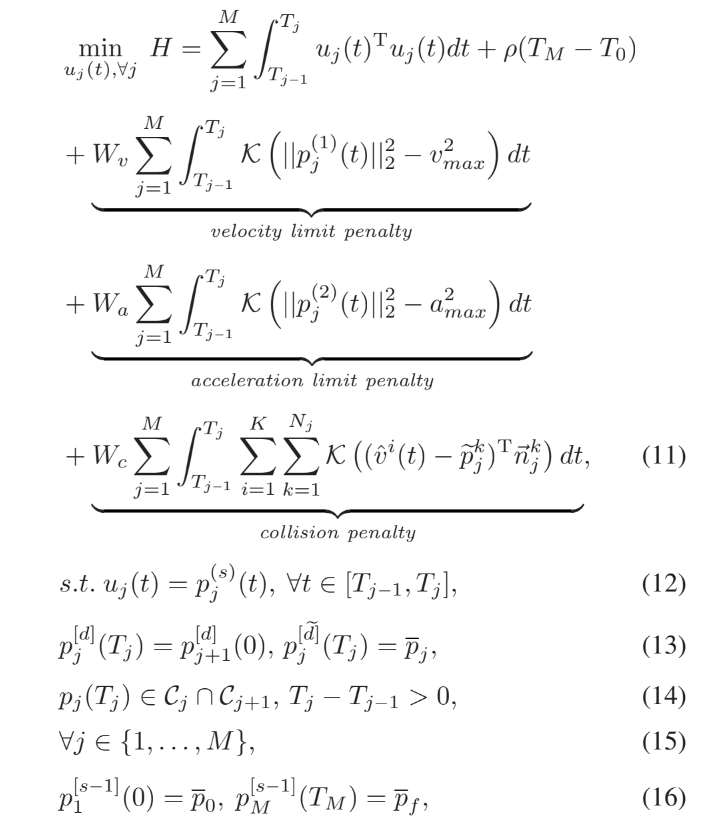
$\mathcal{K}$ 은 cubic penalty function 이다. ($\mathcal{K}=max(\cdot ,0{)}^3$) 나머지 이어지는 수식들도 모두 nonlinear constraints 를 cubic penalty term으로 바꿔 unconstrained optimization 으로 바꾸기 위한 내용으로, GCOPTER 논문과 Yang et al. 에 더 자세히 설명되어 있다.

다만 그 전에는 normalized 한 시간에 대한 각 경로간($j=1,\dots ,M$) 상대적 resolution ${\kappa }_j$ 가 있었는데 여기에서는 고려된 것인지 모르겠다.

또한, 각각 penalty term에 가중치 $W_v,W_a,W_c$ 가 있어서 인지 여태까지의 논문들에서 control effort 에 대해 $u^T(t)Wu(t)$ 로 표현되어 더해진 가중치 $W$ 가 없어졌다.

$$W_c\sum _{j=1}^M{\int }_{T_{j-1}}^{T_j}\sum _{i=1}^K\sum _{k=1}^{N_j}\mathcal{K}(({\hat{v}}^i(t)-{\tilde{p}}_j^k){\overrightarrow{n}}_j^k)dt$$

위 수식에서 $K$ 는 vertex의 갯수이고 $N_j$ 는 hyperplane의 갯수이다.

최적값을 구하기 위해서는 미분 가능해야 하는데 이것에 대해서는 이후 챕터에서 다룬다. 그리고 gradient 표현을 단순하게 하기 위해 smoothness cost ${\sum }_{j=1}^M{\int }_{T_{j-1}}^{T_j}{u}_j(t{)}^T{u}_j(t)dt$ 를 $\mathcal{S}$ 로 표기한다.

C. Gradient Calculation

다항식 궤적에서 계수 행렬을 $C_j\in {\mathbb{R}}^{2s\times 3}$ 로 하고 시간 벡터 $\beta (t)=[1,t,\dots ,t^{2s-1}{]}^T$ 로 하여 아래와 같이 $j$ 번째 궤적을 표현한다.

$$p_j(t)=C_j^T\beta (t-T_{j-1}),t\in [T_{j-1},T_j]\text{\hspace{1em}(17)}$$

그렇다면 전체 궤적에 대한 계수 행렬 (the coefficient matrix) $\mathbf{C}$ 와 시간 할당 벡터 (time allocation vector) $\mathbf{T}$ 를 아래와 같이 정의할 수 있다.

$$\begin{array}{rl}\mathbf{C}& =(C_1^T,C_2^T,\dots ,C_M^T{)}^T\in {\mathbb{R}}^{2Ms\times 3}\\ \mathbf{T}& =(T_1-T_0,T_2-T_1,\dots ,T_M-T_{M-1}{)}^T\\ & =({\delta }_1,{\delta }_2,\dots ,{\delta }_M{)}^T\in {\mathbb{R}}_{+}^M\end{array}\text{\hspace{1em}(18)(19)}$$

그렇다면 앞선 목적함수 $H$ 를 $\mathbf{C},\mathbf{T}$ 의 함수 $H(\mathbf{C},\mathbf{T})$ 로 표현가능하다.

이제 gradient를 계산해보자.

$$\min H=S+\rho T+E_v+E_a+E_c$$

optimization problem 을 위와 같이 매애우 간략히 표현해보면 아래와 같이 gradient 를 표현할 수 있다.

$$\begin{array}{rl}\frac{\partial H(\mathbf{C},\mathbf{T})}{\partial \mathbf{C}}& \simeq \frac{\partial \mathcal{S}}{\mathbf{C}}+\frac{\partial (E_v+E_a+E_c)}{\partial \mathbf{C}}\\ \frac{\partial H(\mathbf{C},\mathbf{T})}{\partial \mathbf{T}}& \simeq \frac{\partial \mathcal{S}}{\partial \mathbf{T}}+\rho 1+\frac{\partial (E_v+E_a+E_c)}{\partial \mathbf{T}}\end{array}\text{\hspace{1em}(20)(21)}$$

수식을 조금 자세히 보면 ${\int }_{T_{j-1}}^{T_j}dt$ 부분이 ${\sum }_{l=0}^{L-1}\frac{{\delta }_j}{L}$ 로 바뀐 것을 알 수 있다. continuous 한 공간에서는 ${\int }_0^{\delta }d\delta$ 으로 표현하므로 이를 dicretization factor $L$ 로 분할해주었다.

smoothness cost $\mathcal{S}$ 는 다항식의 $s$ 차 미분이라서 연산하기 쉬우므로 $E$ 요소들만 미분에 대해 유도해보면 된다.

디테일한 수식전개는 제대로 이해하지 못하여 아래 이미지로 대체한다.

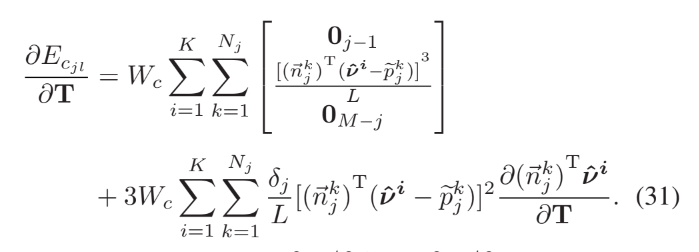
Todo

• gradient 수식 전개 유도

GCOPTER 논문에서 증명한 Optimality condtion 에 의하면 최적해(the minimum control effort peicewise-polynomial trajectory) ${\mathbf{x}}^{\ast }(t)$ 는 중간 지점의 상태 ${\bar{p}}_j\in {\mathbb{R}}^{3(\tilde{d}+1)}$ 가 주어진 $T_j$ 마다 $d$ 차까지 연속적이고 미분가능하다.

그러므로 $2s=\tilde{d}+d+2$ 를 만족해야 한다. 본 연구에서는 $d=4,\tilde{d}=0$ 로 두어 snap 이 항상 연속적이도록 하였다. 중간 지점 ${\bar{p}}_j\in {\mathbb{R}}^3$ 이므로 waypoints $\mathbf{q}=(q_1,\dots ,q_{M-1})\in {\mathbb{R}}^{3\times (M-1)}$ 이 필요하다. (자세한 내용은 앞서 정리한 question 부분 참고. notation 이 한 차수씩 밀려서 달라보이지만 동일한 수식이다.)

Question

• 중간 지점의 상태가 적게 필요할 수록 = $\tilde{d}$ 가 작을 수록
• 연속적이고 마분가능한 차수가 클 수록 = $d$ 가 클 수록 좋은 것 아닌가?
• 그렇다면 $s=3$ 으로 고정되어 있으므로 (초기값, 최종값의 state가 가속도 까지 있으므로 $2\times 3$ boundary conditions 이다.)
• 사실 $d,\tilde{d}$ 는 정해져 있는 것 아닌가?($d$ 가 작아지거나 $\tilde{d}$ 가 커질수록 quality 는 안좋아지므로)

이제 $\mathbf{q},\mathbf{C},\mathbf{T}$ 는 모두 $\mathbf{T}$ 로만 연관되어 정의되는 non-singular mapping matrix $M$ 과 연관지어 진다.

이 $M$ 에 대한 구체적인 정의는 GCOPTER 논문에 나와 있다.

$M$ 이 non-singular 하므로 아래와 같이 정의할 수 있다.

$$\begin{array}{r}M\mathbf{C}=b⟹\mathbf{C}=M^{-1}b\\ b=[{\bar{p}}_0^T,q_1^T,0_{3\times (d+1)},\dots ,q_{M-1}^T,0_{3\times (d+1)},{\bar{p}}_f^T{]}^T\end{array}\text{\hspace{1em}(32)}$$

Question

• $b$ 의 dimension 이 어떻게 되는 것인지? $M$ 을 알아야 정확하긴 하겠지만, 각 요소들의 크기가 달라보인다.
• initial and final state ${\bar{p}}_0,{\bar{p}}_f$나 waypoints $\mathbf{q}$ 는 모두 위치값만 있는 크기 3의 벡터인데, $0_{3\times (d+1)}$ 는 $d=4$ 이므로 snap 까지 포함한 크기이다. 물론 0으로만 이루어져 있긴 하지만…

Solved ?

• 이전 논문에 조금 더 구체적으로 설명되어 있어 참고하여 해결.
• $M(\mathbf{T})\in {\mathbb{R}}^{2Ms\times 2Ms},b(\mathbf{q})\in {\mathbf{R}}^{2Ms\times m}$ 로 되어 있다. 여기서 $m=3$ 이다.
• 본 논문에서는 $\mathbf{C}\in {\mathbb{R}}^{2Ms\times 3}$ 이었으므로 non-singular 한 M과 $b$ 모두 이전 논문과 동일한 크기를 갖는다.
• 그리고 위 질문에 적어놓은 것과 달리 $\bar{p}$ 는 크기가 3인 벡터가 아니라, $s-1$ 차 까지 state 를 가지고 있고 (e.g. $p_1^{[s-1]}(0)={\bar{p}}_0$) 여기서는 위치, 속도, 가속도이다.
• 그렇지만 여전히 $0$ 은 이해되지 않는다. $q$ 가 위치값만 있으므로 나머지 속도, 가속도에 대해 영벡터를 넣어준 것이라면 $d+1$ 이 아니라 $s-2$ 혹은 2 여야 하지 않나?
• 그리고 $b(\mathbf{q})\in {\mathbf{R}}^{2Ms\times m}$ 이 맞아 떨어지려면 $2M$ 개의 state 정보가 있어야 하는데, $\bar{p}$ 는 $M$ 개가 맞지만, $q$ 는 $M-1$ 개 이다… 참고

어쨌든, 궤적은 $\mathbf{q},\mathbf{T}$ 에 의해 완전히 정해진다. (uniquely determined)

그래서 최적화 문제와 gradient 계산을 아래와 같이 표현할 수 있다.

여기서 필요로 하는 $\frac{\partial C}{\partial q},\frac{\partial C}{\partial T}$ 는 $O(M)$ 의 복잡도로 얻어낼 수 있음을 이전 논문에서 증명하여 여기서도 linear complexity 라고 언급하였다. 이로써, unconstrained optimization problem이 되어 quasi-Newton method로 풀어낸다.

D. High-Performance Implementation of SE(3) Planner

경로 생성에 필요한 연산은 각각의 $M$ 조각의 다항식 궤적을 $L$ 만큼 이산화하여 연산하므로 $L$ 에 연관된 상수 시간 $U$ 를 정의하였을 때, 전체 궤적의 gradient 의 시간복잡도는 $U\cdot M$ 로 표현할 수 있다.

그러나 큰 스케일의 경로 생성에서는 여전히 큰 시간 소요에 해당할 수 있고, 각각의 constraint point에 대해 gradient를 계산하는 것이 독립적이므로 (i.e. $\sum$) 이를 병렬 구조로 나눠 GPU를 통해 가속한다.

그러면 각 iteration에 걸리는 연산 시간은 $\frac{U}{L}$ 로 감소한다.

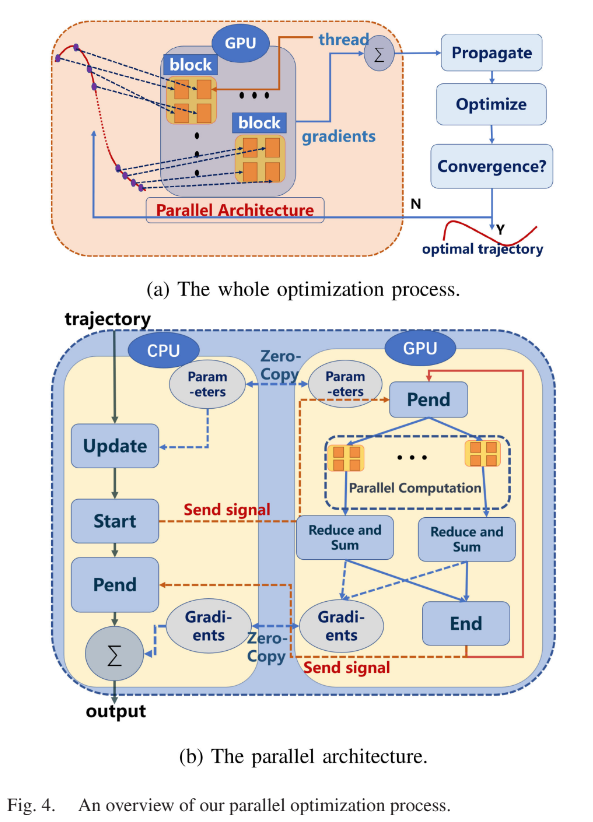
그리고 zero-copy로 디바이스에 넘겨주어 데이터 전송에 걸리는 시간을 줄였다고 한다. 이런 부분은 GPU 최적화 관련이지만, 논문에 같이 나오는 부분이 신기했다.

구체적인 과정은 아래와 같다.

1. 최적화 문제가 만들어지면 GPU 커널을 실행한다.
2. 각 iteration 마다 궤적 parameter 에 대한 정보를 업데이트 하고 이에 대한 신호를 CPU 에서 GPU 로 보낸다. $j$ 번째 궤적 ($j=1,\dots ,M$) 의 $l$ 번째 discretization point ($l=0,\dots ,M-1$) 의 gradient $g_{jl}$ 는 각각 $j$ 번째 블록의 $l$ 번째 쓰레드에 할당되어 연산된다. local shared memory 를 사용하였다고 한다.(GPU 최적화 부분, 메모리 오버헤드를 줄인다.)
3. 각 블록의 local memory 에 저장된 gradient 를 reduce and sum 연산을 하여 ${\sum }_{l=0}^{L-1}{g}_{jl}$ 을 얻는다.
4. 그리고 연산이 완료되면 zero-copy 되어 있는 gradient 가 모두 합산되어 모든 궤적에 대한 gradient 가 얻어진다. ${\sum }_{j=1}^M{\sum }_{l=0}^{L-1}{g}_{jl}$

SE(3) Drone Racing Simulation

구체적인 적용과 시뮬레이션 구조, 타 알고리즘과의 비교 및 메트릭은 생략.

Evaluation

여기 챕터에서도 크게 살펴볼 내용은 없지만, CUDA 블록에 대한 구체적인 설명이 있다.

RTX 2060 GPU 를 사용하였고 $T_r\cdot N$ 코어를 사용하였다. $T_r$ 은 64로 선택하여 경로 분할을 $N$ 조각으로 나누었다고 한다.

아마 블럭 수와 내부에서 matrix multiplication 연산을 최적화한다면 더 빠른 연산을 기대할 수도 있어 보인다.