[IROS '17] Search-based Motion Planning using Linear Quadratic Minimum Time Control

이전 Post인 RA-L 논문 저자의 선행 연구를 살펴보고자 한다.

Arxiv

Introduction & Related Works

이전에서도 언급되었지만 추후 공부할 선행 논문들을 리스트업해보았다.

Quadrotor의 differential flatness를 이용한 jerk 혹은 snap을 통한 제어 논문

1. D. Mellinger and V. Kumar, “Minimum snap trajectory generation and control for quadrotors,” in Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), 2011.

2. M. Hehn and R. D’Andrea, “Quadrocopter trajectory generation and control,” IFAC Proceedings Volumes, vol. 44, no. 1, 2011.

3. M. Mueller, M. Hehn, and R. D’Andrea, “A computationally efficient motion primitive for quadrocopter trajectory generation,” IEEE Trans. on Robotics (T-RO), vol. 31, no. 6, pp. 1294–1310, 2015.

이러한 방식은 시간에 대한 다항식으로 궤적을 구성하여 $\mathbf{x}=[p^T,v^T,a^T{]}^T$ 와 같이 state space를 구성하고 control input을 $j$ 혹은 snap ( 이 경우 $j^T$ 도 $\mathbf{x}$ 에 포함)을 사용한다.

time-optimal한 궤적 생성에 관한 논문들

4. Y. Bouktir, M. Haddad, and T. Chettibi, “Trajectory planning for a quadrotor helicopter,” in 16th Mediterranean Conference on Control and Automation, 2008.

5. J. Jamieson and J. Biggs, “Near minimum-time trajectories for quadrotor UAVs in complex environments,” in IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), 2016, pp. 1550–1555.

하지만 장애물을 고려하게 되면 constraint 부분이 추가되면서 더 어려운 문제가 된다. (특히 real-time application에서)

mixed integer optimization 방식을 사용한 아래 논문들도 있지만, 연산 속도는 여전히 challenging 하다.

Mixed integer optimization

6. D. Mellinger, A. Kushleyev, and V. Kumar, “Mixed-integer quadratic program trajectory generation for heterogeneous quadrotor teams,” in Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), 2012.

7. R. Deits and R. Tedrake, “Efficient mixed-integer planning for UAVs in cluttered environments,” in Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), 2015.

Quadratic programming / real-time / collision-free trajectory generation

8. C. Richter, A. Bry, and N. Roy, “Polynomial trajectory planning for aggressive quadrotor flight in dense indoor environments,” in Robotics Research. Springer, 2016, pp. 649–666.

9. S. Liu, M. Watterson, S. Tang, and V. Kumar, “High-speed navigation for quadrotors with limited onboard sensing,” in 2016 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2016.

10. S. Liu, M. Watterson, K. Mohta, K. Sun, S. Bhattacharya, C. J. Taylor, and V. Kumar, “Planning dynamically feasible trajectories for quadrotors using safe flight corridors in 3-D complex environments,” IEEE Robotics and Automation Letters, vol. 2, no. 3, pp. 1688–1695, July 2017.

11. J. Chen, T. Liu, and S. Shen, “Online generation of collision-free trajectories for quadrotor flight in unknown cluttered environments,” in 2016 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2016, pp. 1476–1483.

위 논문들은 collision-free한 geometric 경로를 만든 후, 부분적으로 dynamically-feasible한 궤적을 최적화한다.(optimizing it locally to obtain a dynamically-feasible time-parametrized trajectory)

문제는 geometric한 경로는 dynamics를 고려하지 않고 단순 공간적인 정보만 고려하여, 이후 최적화를 진행하더라도 geometric 경로들이 이루는 homology class에 갇히게 되어 locally optimal 하다.

따라서 본 논문은 전역 경로(global trajectory)에 대해 collision-free, dynamically-feasible, minimum-time, smooth trajectories, real-time 한 최적화 방법을 제안하고자 한다.

geometric 경로 대신 Optimal Control Problem(OCP)를 풀어 얻은 motion primitives의 집합으로 경로들을 만들고 이를 그래프 탐색 방식으로 적절한 경로를 선정하고자 한다.

그래프 탐색이 비효율적이지만 본 논문은 tight lower bound(but heuristic) 로 탐색을 빠르게 만들었다.

Problem Formulation

대다수의 내용은 이전 Post의 Formulation과 거의 동일하다. 따라서 디테일한 설명은 생략한다.

${\mathcal{X}}^{free}={\mathcal{P}}^{free}\times {\mathcal{D}}^{free}$ 로 정의한다. ${\mathcal{P}}^{free}$ 는 obstacle-free한 위치들이 이루는 공간(or 집합)이고 ${\mathcal{D}}^{free}$ 는 dynamics를 고려한 것이다. dynamics는 differential flatness를 이용해 $[\dot{x},\ddot{x},\dots ]$ 의 최소 최댓값으로 한다.

Quote

12. D. W. Mellinger, “Trajectory generation and control for quadrotors,” Ph.D. dissertation, University of Pennsylvania, 2012.

위 논문을 포함한 여러 연구에서 quadrotor의 differential flatness를 통해 1D control input과 time-parametrized 다항식 궤적이 가능함을 보였다. (수식 생략, 이전 Post 수식 (8) 참고)

그리고 이러한 다항식 궤적을 미분함으로써 시간 $t$ 에서의 state $x(t)$ 를 구성하였다. control input $u$ 또한 이 궤적의 $n$ 번째 미분으로 얻을 수 있고 이를 간단히 표현하면 아래와 같이 표현가능하다.

$$\begin{array}{rl}\dot{x}& =Ax+Bu\\ A& =\left[\begin{array}{ccccc}0& I_3& 0& \dots & 0\\ 0& 0& I_3& \dots & 0\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& \dots & \dots & 0& I_3\\ 0& \dots & \dots & 0& 0\end{array}\right],B=\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ I_3\end{array}\right]\end{array}\text{\hspace{1em}(2)}$$

시간에 대해 differentially flat한 system에서 사용되는 equation 이다.

*Problem 1

주어진 초기 state $x_0\in {\mathcal{X}}^{free}$ 과 목표 지역 ${\mathcal{X}}^{goal}\subset {\mathcal{X}}^{free}$ 에 대해 다항식 궤적의 계수를 찾는다

$$\begin{array}{rl}& \underset{D,T}{\min }=J(D)+\rho T\\ s.t.\dot{x}(t)& =Ax(t)+Bu(t),\forall t\in [0,T]\\ x(0)& =x_0,x(T)\in {\mathcal{X}}^{goal}\\ x(t)& \in {\mathcal{X}}^{free},u(t)\in \mathcal{U},\forall t\in [0,T]\end{array}\text{\hspace{1em}(4)}$$

이 때 $D\in {\mathbb{R}}^{3\times (K+1)}$ 은 다항식 계수 $d_i,i=1,\dots ,K$ 가 이루는 $K\times 1$ 열벡터이다. $J$ 는 이전 Post에서처럼 control effort 이다. $\rho \ge 0$ 는 궤적 비행 시간 $T$ 와 smoothness(=control effort) $J$ 를 밸런싱하는 가중치이다.

위와 같이 목적함수를 설정한 것에 대해서는 아래 그림으로 설명하고 있다.

즉, (a)와 (b)는 소요되는 effort가 다르지만 경로 비행에 걸리는 시간은 동일하다. 둘다 적은 시간이지만 (a)가 더 우수한 경로임을 알 수 있다. effort가 훨씬 적은 (c)는 (a)보다 시간이 더 소요되었다. 따라서 저자는 두 가지를 모두 적절히 고려해야 한다고 주장한다.

Note

• 너무 heuristic한 방식이 아닐까? 고려해야 하는 요소들이 더 있거나 $\rho$ 로만 조절하기에 부적절하다거나

Problem 1은 state에 대한 constraints가 더해진 Linear Quadratic Minimum-Time problem 이다.

Quote

13. E. Verriest and F. Lewis, “On the linear quadratic minimum-time problem,” IEEE Transactions on Automatic Control, vol. 36, no. 7, pp. 859–863, 1991.

이 $x(t)\in {\mathcal{X}}^{free},u(t)\in \mathcal{U},\forall t\in [0,T]$ 부분이 풀기 어려운 부분인데, 만약 이 부분을 덜어낼 수 있다면 Pontryagin’s minimum principle에 의해 최적해를 구할 수 있게 된다.

본 논문은 이 safety constraints 부분을 deterministic shortest path problem 으로 바꿔서 해결하였다고 한다. (with $3n$ dimensional state space $\mathcal{X}$, 3 dimensional control space $\mathcal{U}$)

Quote

14. D. Bertsekas, Dynamic Programming and Optimal Control. Athena Scientific, 1995.

또한, $\mathcal{U}$ 가 3차원이고, 정해진 시간에 discretized 된 공간에서 경로 계획을 수행하므로 sampling-based 보다 search-based가 더 낫다고 한다.

Optimal Trajectory Planning

A. Motion Primitives

이전 섹션에서 dterministic shortest path problem으로 바꾸고, search-based planning을 한다는 것은 결국 lattice discretization을 한다는 의미이기도 하다.

따라서 control set $\mathcal{U}$ 를 ${\mathcal{U}}_M:=\{u_1,\dots ,u_M\}$ 으로 이산화한다. 각 축의 $[0,{\mu }_{max}]$에 대해 $\mu$ 개의 샘플을 고르면 $d_i:=u_{max}/\mu$ 의 간격이 되어 $M=(2\mu +1{)}^3$ 개의 motion primitive 들이 만들어진다.(=필요하다)

여기서 $M=(2\mu +1{)}^3$ 인 이유는 각 $[x,y.z]$ 축에 대해 $\mu$ 개의 샘플이 양수, 음수에 0까지 하여 $2\mu +1$ 개이기 때문이다.

이를 초기 state $x_0$ 을 고려하여 이전 Post 수식 (8)을 작성해보면 아래와 같다.

$$p_D(t)=u_m\frac{t^n}{n!}+\cdots +a_0\frac{t^2}{2}+v_{0}t+p_o$$

주의할 점은 이전 Post 수식 (8)에서는 $p_D(t)$ 대신 $\mathbf{x}(t)$ 를 사용하였다. (jerk control에서는 $n=3$ 이므로 이전 Post 수식(10) 참고하면 같은 수식임을 알 수 있다.)

추가적으로, control $u(t)$ 는 마지막 $n$ 번째 미분값을 사용하고 상수임을 인지하자.

본 논문에서는 $\dot{x}(t)=Ax(t)+B$ 를 이용하여 아래와 같이 일반화 하였다.

$$x(t)=e^{At}{x}_0+[{\int }_0^t{e}^{A(t-\rho )}Bd\rho ]u_m$$

B. Induced Space Discretization

Proposition 1. The motion primitives defined in the previous section induce a discretization on the state space $\mathcal{X}$

Proof. 주어진 초기 state $x_0$ 과 $k$ 개의 input $u_1,\dots ,u_k$ 가 매 $\tau$ 마다 적용된다. 그러고 난 뒤의 마지막 state $x(k\tau )$ 는 아래와 같다.

이 때 $F(\cdot )=e^{At}$ 이고 $G(\cdot )={\int }_0^t{e}^{A(t-\rho )}Bd\rho$ 이다. ($A,B$ 는 수식 (2) 참고)

Question

• 여기 증명 수식 정리 이해 못함…

결론적으로 control input이 이산화되면서 state space까지 이산화됨을 보였고, 이를 통해 $x_0$ 부터 $\tau$ 동안 primitive를 적용하여 $M$ 개의 가능한 state 들을 그래프로 구성할 수 있다.

그리고 $2\tau$ 에서는 $M^2$ 개의 state 들이 가능하므로 $k\tau$ 에서는 $M^k$ 개의 state가 가능하다.

구성한 그래프 $G(S,\mathcal{E})$ 는 이산화된 state $s$ 들의 집합 $S$ 와 이들을 연결하는 edge $e:=(u_m,\tau )\in \mathcal{E}$ 로 정의한다.

그 후 위와 같은 알고리즘로 그래프를 확장하고 cost function $C(s)$ 를 구성한다.

알고리즘은 위에서 설명한 대로 모든 control input $u_m\in {\mathcal{U}}_M$ 에 대해 primitive를 구하고 safety constraint를 만족하면 $m$ 개의 edge와 이어지는 state가 형성된다.

이를 목표 state인 $s_g\in {\mathcal{X}}^{goal}$ 까지 수행하므로 $T=N\tau$ 라고 하였을 때 ${\sum }_{i=0}^N{m}^i,\forall s_m(t)\subset {\mathcal{X}}^{free}$ 개의 노드들을 가지는 그래프가 된다…!!

본 논문에서 $s_0$ 를 $x_0$ 라고 하였고 이 수식과 Algorithm 1의 4번째 수식과 동일하므로 $x(T)=s_g$ 이다.

Note

• $t\in [0,\tau ]$ 에서의 $e_m(t)$ 를 safety constraints를 만족하면 $e_m(\tau )$ 로 고려한다…(Algorithm 6번째 라인)
• 이는 discretizaiton의 한계..?

Proposition 2 Algorithm 1의 4~6번째 라인에 대한 내용 motion primitive $u_{i,j}\in {\mathcal{U}}_M$ 을 두 연속된 state $s_i,s_j\in S$ 를 잇는 edge라고 했을 때, 이로부터 만들어진 $s_j=F(\tau )s_i+G(\tau )u_{i,j}$ 는 optimal 하다.

이 때 $F(\cdot )=e^{At}$ 이고 $G(\cdot )={\int }_0^t{e}^{A(t-\rho )}Bd\rho$ 이다. ($A,B$ 는 수식 (2) 참고)

Proof.

논문에서는 증명을 Appendix B로 하여 언급된 Proposition 3가 아직 나오지 않았다. 어차피 증명 이해를 못하였으므로…일단 패스

Question

• Proposition 1과 마찬가지로 증명 이해 못함

C. Deterministic Shortest Trajectory

앞선 A와 B 섹션에서 이산화와 그래프 구성을 통해 수식 (4)를 그래프 탐색 문제로 바꿀 수 있다.

continuous space에서의 $u(t)$ 를 $T=N\tau ,\forall N\in {\mathbb{Z}}^{+}$ 과 $u_k\in {\mathcal{U}}_M,\text{for}k=0,\dots ,N-1$ 에 대해 아래와 같이 표현할 수 있다.

$$u(t)=\sum _{k=0}^{N-1}=u_k{1}_{t\in [k\tau ,(k+1)\tau ]}$$

요약하면 control trajectory (앞선 다항식의 $n$ 차 미분)을 motion primitive의 조합으로 구성하는 것이다. 이것은 앞선 Problem 1 를 deterministic shortest path problem 으로 만든다.

Problem 2 주어진 초기 state $x_0\in {\mathcal{X}}^{free}$, 목표 지역(goal region) ${\mathcal{X}}^{goal}\subset {\mathcal{X}}^{free}$ 과 $\tau >0$ 의 시간 간격을 갖는 motion primitive의 유한 집합 ${\mathcal{U}}_M$ 에 대해 아래의 조건을 만족하는 $N$ 개의 연속된 $u_i,i=0,\dots ,N-1$ 를 선택한다.

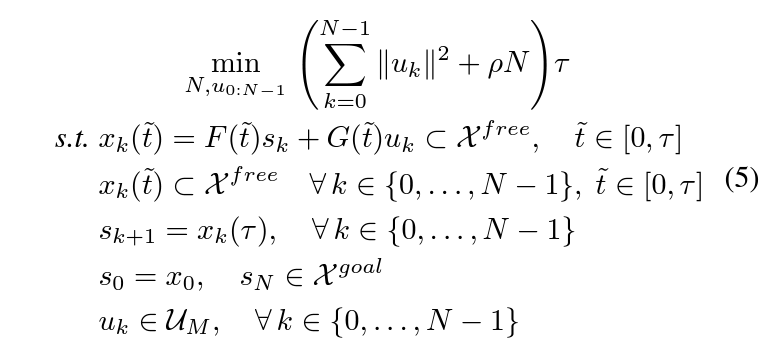
결국 Problem 1의 constrained version (=discretization)이기 때문에 Problem 2 는 최적해의 상한이 됨을 알 수 있다.

그리고 이 문제는 search-based 혹은 sampling-based로 효율적으로 풀 수 있으나, 본 논문에서는 전자인 search-based motion planning이 유한한 시간내의 최적값을 찾는 것을 보장해주므로 이 방식을 선택하고 그 중 $A^{\ast }$ 방식을 선택하였다.

D. Heuristic Function Design

Problem 2를 위한 효율적인 그래프 탐색에는 optimal cost function을 근사할 수 있는 heuristic function이 필요하다.

이 heuristic function은 admissible, informative 해야 한다.

A heuristic function $h$ is admissible if it underestimates the optimal cost-to-go from $x_0$, i.e., $0\le h(x_0)\le C^{\ast }(x_o,{\mathcal{X}}^{goal}),\forall x_0\in \mathcal{X}$.

A heuristic function $h$ is consistent if it satisfies the triangle inequality, i.e., $h(x_0)\le C^{\ast }(x_0,\{x_1\})+h(x_1),\forall x_0,x_1\in \mathcal{X}$.

이러한 조건을 이해한 바로는, optimal cost function은 cost function의 최솟값이므로 $x_0$ 부터 ${\mathcal{X}}^{goal}$ 로의 요소들인 $h(\cdot )$ 은 더 작아야 하고 각각의 부분들, 예를 들어 $x_k$ 에서 $x_{k+1}$ , 에서도 이를 계속 만족해야 한다는 것이다.

consistent 부분 조건 식을 admissible을 만족하는 함수에 대해 다시 써본다면 다음과 같다.

$$h(x_0)\le C^{\ast }(x_0,\{x_1\})+h(x_1)\le C^{\ast }(x_0,\{x_1\})+C^{\ast }(x_1,{\mathcal{X}}^{goal})=C^{\ast }(x_o,{\mathcal{X}}^{goal}),\forall x_0,x_1\in \mathcal{X}$$

이러한 heuristic $h(\cdot )$ 은 tight approximation of the optimal cost 라고 할 수 있다.

본 논문에서는 Problem 2의 하한이 Problem 1의 최적해이므로, Problem 1의 relaxed version을 풀어냄으로써 좋은 heuristic function을 얻을 수 있다고 한다.

Question

• 그렇다면 Problem 1 $\le h(\cdot )\le$ Problem 2 인 건가?

그 방법으로 본 논문은 수식 (4)의 제한조건 $x(t)\in {\mathcal{X}}^{free},u(t)\in \mathcal{U}$ 를 시간 $T$ 에 대한 조건으로 바꾸는 것을 제안하였다.

1) Minimum Time Heuristic 앞서 ${\mathcal{D}}^{free}$에 대한 constraints를 다루면서 속도, 가속도, jerk에 대한 최대값을 두었기 때문에 목표 지점에 도달하기 위한 최소 가능 시간 $\bar{T}$ 를 도입할 수 있게 된다.

예를 들어, ${\mathcal{X}}^{goal}$ 안에 있는 가장 가까운 $x_f$ 를 도달할 수 있는 최소 시간은 ${\bar{T}}_v:=\frac{\Vert p_f-p_0{\Vert }_{\infty }}{v_{max}}$ 이다. 이와 마찬가지로 최대 가속도 $a_{max}$ 를 가질 때, 아래 조건을 만족하는 시간 ${\bar{T}}_a$ 보다 더 빠르게 목표 $x_f:=[p_f^T,v_f^T{]}^T$ 에 도달할 수 없다.

$$\begin{array}{rl}& mi{n}_{{\bar{T}}_a,a(t)}{\bar{T}}_a\\ \text{s.t.}\Vert a(t)\Vert & \le a_{max},\forall t\in [0,T]\\ p(0)& =p_0,v(0)=v_0\\ p({\bar{T}}_a)& =p_f,v({\bar{T}}_a)=v_f\end{array}$$

이는 minimum-time (Brachistochrone) OCP with input constraints로 3차원에서 풀기는 어렵지만 각 축에 대해서 적용한다면 가능하다. (i.e. ${\bar{T}}_a^x,{\bar{T}}_a^y,{\bar{T}}_a^z$)

그래서 최소로 도달 가능한 시간 $\bar{T}$ 를 $\bar{T}:=\max \{{\bar{T}}_v,{\bar{T}}_a^x,{\bar{T}}_a^y,{\bar{T}}_a^z,{\bar{T}}_j,\dots \}$ 로 정의하지만 더 쉽게 계산하기 위해 $\bar{T}={\bar{T}}_v$ 로 간단히 취한다. (??)

Question

• 3차원에서 풀기 어렵다는 의미가 모든 $x,y,z$에 대하여 ${\bar{T}}_a^{\ast }$ 를 구하기 어렵다는 의미인가?
• 만약 그렇다면 각 축에 대한 값으로 바꿔서 취하는 것은 $\sqrt[3]{{\bar{T}}_a^x}$ 와 같이 변형되어야 하지 않나?
• jerk (혹은 가속도) 제어에서 $x(t)\in {\mathcal{X}}^{free},u(t)\in \mathcal{U}$ 를 $\bar{T}={\bar{T}}_v$로만 퉁치는게 가능한가?

이를 모두 정리하여 heuristic function을 찾기위한 OCP를 아래와 같이 정리할 수 있다.

$$\begin{array}{rl}& \underset{D,T}{\min }=J(D)+\rho T\\ s.t.\dot{x}(t)& =Ax(t)+Bu(t),\forall t\in [0,T]\\ x(0)& =x_0,x(T)\in {\mathcal{X}}^{goal}\\ T& \ge \bar{T}\end{array}\text{\hspace{1em}(6)}$$

Problem 1과 비교하면 $x(t)\in {\mathcal{X}}^{free},u(t)\in \mathcal{U},\forall t\in [0,T]$ 부분이 $T\ge \bar{T}$로 대체되었다.

$J(D)\ge 0$ 이므로 최적해 $C^{\ast }(\cdot )$ 의 하한을 아래와 같이 얻을 수 있다.

$$C^{\ast }(x_0,{\mathcal{X}}^{goal})=J(D^{\ast })+\rho T\ge \rho {\bar{T}}_v$$

그렇다면 이산화된 공간(discretized space)에서의 node 인 $s_0,s_f\in S$ 에서 heuristic function $h_1(s_0)=\rho {\bar{T}}_v$ 로 둘 수 있고, admissible 하고 consistent 함을 쉽게 보일 수 있다. (아래 수식과 이전 내용 참고

$$h_1(s_0)=\rho {\bar{T}}_v=\rho \frac{\Vert p_f-p_0{\Vert }_{\infty }}{v_{max}}\text{\hspace{1em}(7)}$$

admissible: $h_1(s_0)\le C^{\ast }(x_0,{\mathcal{X}}^{goal})=J(D^{\ast })+\rho T$ consistent: $todo$

2) Linear Quadratic Minimum Time $h_1(x_0)$ 은 연산하기도 쉽고 속도 조건도 고려하긴 하지만, control effort를 고려하지 않아 매우 tight lower bound 라고 하기는 어렵다.

대신, 수식 (6)이 the classical Linear Quadratic Minimum-Time Problem에 해당하므로 [15] $T\ge T^{\ast }$ 조건을 활용하여 최적해를 찾아낼 수 있다. [15, Thm.2.1]

Quote

15. E. Verriest and F. Lewis, “On the linear quadratic minimum-time problem,” IEEE Transactions on Automatic Control, vol. 36, no. 7, pp. 859–863, 1991.

위 논문을 참고하여 제시한 것으로 보이는 Proposition 3. 가 나오는데 제대로 이해하기 어려웠다. 요 내용은 앞서서도 이해하지 못한 Appendix B에서도 참조하고있다.

Proposition 3.

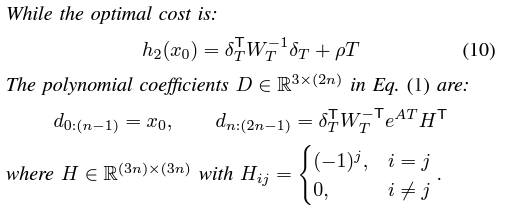
Todo

Proposition 3 이해

결론적으로는 이렇게 얻은 heuristic function $h_2(\cdot )$ 은 이전의 $h_1$ 보다 더 낫다고 할 수 있다. 또한 $h_2(x_0)\le$ Problem 1의 최적해 $\le$ Problem 2의 최적해 이므로 admissible 하다고 할 수 있다.

그리고 이것을 속도, 가속도 제어에 대해 각각 아래와 같이 풀어내었다. (jerk 제어는 RA-L ‘18 논문에 설명되어있다.)

결국 최적해는 $T$ 에 대한 다항식이므로 아래와 같이 $C^{\ast }(T{)}^{\prime }=0$ 의 양의 실수해를 찾는 문제가 된다.

$$\begin{array}{rl}& T^{\ast }=\arg \underset{T}{\min }{C}^{\ast }(T)\\ s.t.& T\ge \bar{T}\end{array}$$

E.Collision Checking

앞서 Alg. 1에서 그래프의 edge $e(t)=[p(t{)}^T,v(t{)}^T,a(t{)}^T,\dots {]}^T$ 가 $e(t)\subset {\mathcal{X}}^{free},\forall t\in [0,\tau ]$ 인지 확인해야 했다.

${\mathcal{X}}^{free}$ 는 장애물 충돌이 없는 ${\mathcal{P}}^{free}\subset {\mathbb{R}}^3$ 과 dynamics 조건 ${\mathcal{D}}^{free}\subset {\mathbb{R}}^{3(n-1)}$ 을 만족해야 한다.

${\mathcal{D}}^{free}$ 는 differential flatness를 이용하여 아래와 같이 정리된다.

$$\begin{array}{rl}& \Vert v{\Vert }_{\infty }\le v_{max},\forall t\in [0,\tau ]\\ (v,a,\dots )\subset {\mathcal{D}}^{free}⟺& \Vert a{\Vert }_{\infty }\le a_{max},\forall t\in [0,\tau ]\\ & ⋮\end{array}\text{\hspace{1em}(11)}$$

$v,a,\dots$ 모두 다항식이므로 극값을 찾아 경계값과 비교하여 쉽게 풀어낼 수 있다.

그에 반해, ${\mathcal{P}}^{free}$ 는 풀기 어려운 부분인데 본 논문에서는 Occupancy Grid Map 을 사용하였고 $\tau$ 시간 안에서 $I$ 개의 위치값을 선택하여 충돌 여부를 확인하였다.

즉 주어진 경로 $p(t),t\in [0,\tau ]$ 와 grid map resolution $R$ 에 대해 $P:=\{p(t_i)|t_i\in [0,\tau ],i=0,\dots ,I\}$ 를 아래 조건을 만족하도록 선택한다.

$$t_i:=\frac{i}{I}\tau \text{such that}\frac{\tau }{I}{v}_{max}\ge R\text{\hspace{1em}(12)}$$

Note

• weak한 Collision Checking 라고 생각하는데 어떻게 edge case를 만들고 어떻게 개선할 수 있을까?

위 조건은 두 연속된 샘플 간의 최대 거리가 지도의 resolution을 넘지 않도록 한다. 그러나 이러한 방식은 $R$ 보다 짧은 cell에 있는 원래의 궤적 $p(t)$의 일부를 놓치게 만들 수도 있다.

Trajectory Refinement

trapezoid velocity profile은 로봇이 경로를 따라가는 것을 표현하는데 널리 쓰인 방식이다. 자세한 설명은 아래 영상으로 대체.

이 방식은 전체 시간을 쉽게 파악할 수 있어 motion planning에 필요한 time allocation을 가능하게 한다. 그러나 dynamics를 고려하지 않고 particle로 근사하므로 주어진 경로과 많은 차이를 일으키기도 한다.

본 논문에서 제시한 경로 계획은 OCP를 풀어 collision-free하고 time-reaching하므로 이를 고차원에서의 경로 계획에 활용하는 방식을 제안한다. (higher dimension = smoother)

그래서 주어진 $s_0,s_g$ 와 중간 경로점 $p_k,k\in \{0,\dots ,N-1\}$ 에 대해 QP를 풀어 refined trajectory $x^{\ast }(t)$ 를 얻는다.

$$\begin{array}{rl}& \underset{D}{\min }\sum _{k=0}^{N-1}{\int }_0^{{\tau }_k}\Vert p_{Dk}^{(n)}(t){\Vert }^{2}dt\\ \text{s.t.}{x}_0(0)& =s_0,x_{N-1}({\tau }_{N-1})=s_g\\ x_{k+1}(0)& =x_k({\tau }_k),k\in \{0,\dots ,N-2\}\\ p_{Dk}({\tau }_k)& =p_k,k\in \{0,\dots ,N-1\}\end{array}\text{\hspace{1em}(13)}$$

여기서 각 경로의 요소의 시간인 ${\tau }_k$ 는 이전에 계획된 경로(lower dimension)에서 얻어진다. 수식에 대한 이해를 조금 적어보자면, 논문에서는 앞서 제시된 notation들을 모두 설명생략하였지만 $D$ 는 계수들이고 $x(\cdot )$ 은 state 이다. 그러므로, 이전에 얻은 각 waypoint 들과 그 시간 ${\tau }_k$ 를 만족하기 위한 control effort의 최소값을 찾고자 하는 것이다. ($p^{(n)}(t)$ 이 control input 이지 않나…)

수식(13)은 논문 [1]에서 풀이가 나타나있어 자세한 내용은 생략하고 결과만 아래 그림으로 보여주었다.

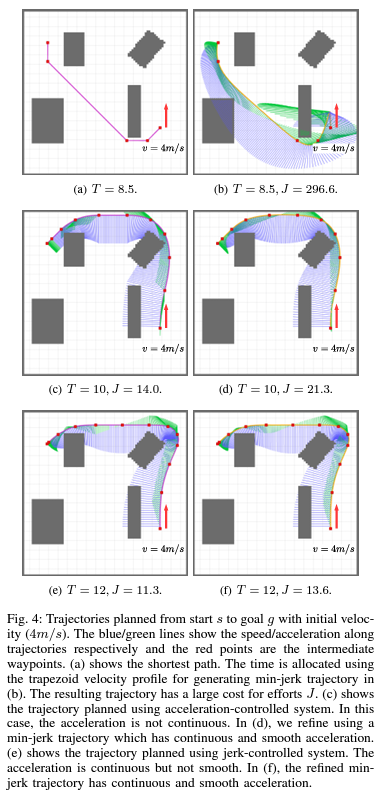
요약하면 trapezoid velocity profile로 만들어진 경로는 control effort가 크게 나왔다. 본 논문이 제시한 refinement 를 통해 적절한 시간과 훨씬 적은 control effort로 경로를 계획할 수 있으며 또한 smoother한 경로를 만들 수 있었다.

하지만 이러한 과정으로 smoother한 경로를 얻었지만 안전하지 않거나 infeasible 할 수 있다고 언급하였다.(!!)

Experimental Results

대부분 생략하고 인상깊은 내용만 요약

A. Heuristic Function

$h_1$ 과 $h_2$ 를 비교하고 Dijkstra 와 $A^{\ast }$ 를 적용.

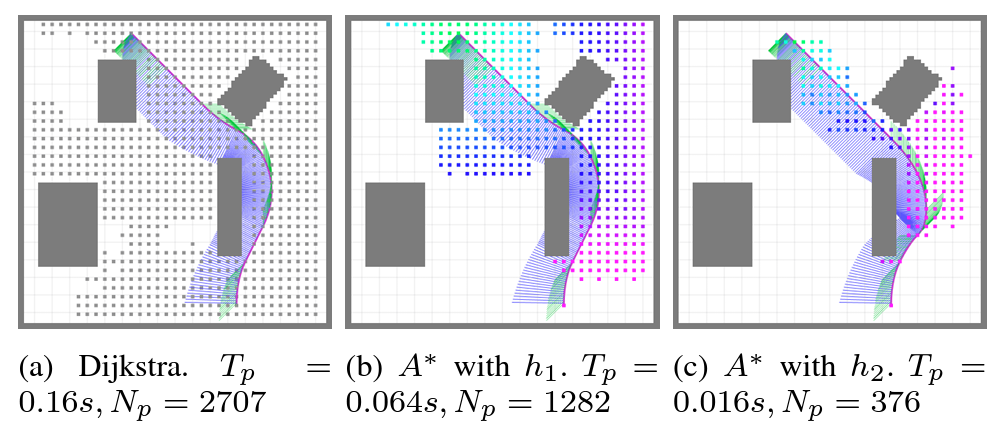
$h_2$ 가 훨씬 적은 노드들을 빠르게 탐색하였다. (without loss of optimality) 하지만 dimension 이 높아질 수록(i.e. 4 이상) 다항식의 해를 찾는게 점점 어려워진다.

최대 속도가 낮은 경우에는 $h_1$ 을 쓰는 것으로 충분하다고 한다. 앞서 $h_1$ 은 dynamics를 고려하지 않지만 충분하다고 한다.

C. Re-planning and Comparisons

널리 쓰이는 Receding Horizon Control(RHC) 방식과 본 논문이 제안한 방식을 비교하였다.

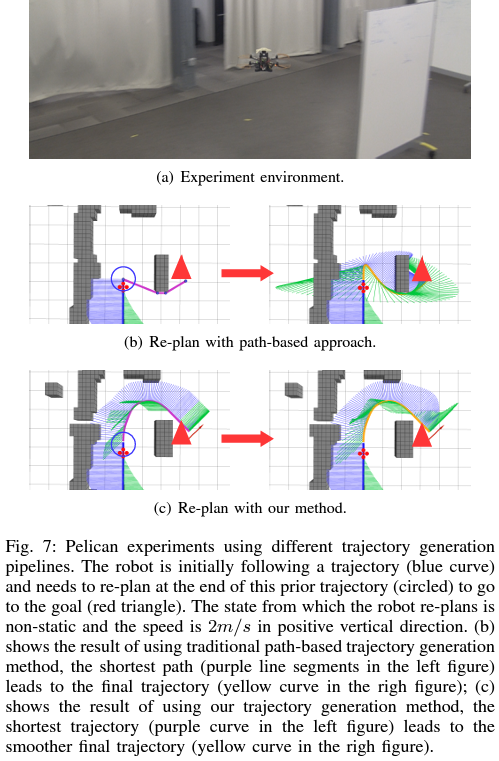
Question

• 더 smoother 한 것은 알겠지만, 걸린 시간과 control effort 는 왜 비교하지 않았을까?

논문을 보고 이전 RA-L 논문을 조금 더 잘 이해할 수 있게 되었다. 다른 후속 논문들은 더 어떻게 발전하였는지 코드로 어떻게 구현했는지 궁금해졌다.

정리 끄읏.