ACADO Toolkit study

Tutorials

A Guiding Example: Time Optimal Control of a Rocket Flight

아래는 첫번째 예제에 대한 수식이다.

x (\cdot), u (\cdot) min s.t. \overset{x}{˙} (t) x (0) \underline{u} (t) \underline{x} (t) 0 \int T (∣∣ x (t) ∣ ∣_{Q}^{2} + ∣∣ u (t) ∣ ∣_{R}^{2}) d t + ∣∣ x (T) ∣ ∣_{P}^{2} = f (x (t), u (t)), = x_{0}, \leq u (t) \leq \overline{u} (t), \leq x (t) \leq \overline{x} (t), for all t \in [0, T]

간단한 로켓 모델에 대해 differential states $s, v, m$ 은 각각 비행거리, 속도, 로켓 질량이다.

코드는 다음 링크에서 참고하도록 한다.

include/acado_gnuplot/gnuplot_window.hpp: no such file or directory

첫 예제를 빌드 할 때 바로 에러가 발생하였다.

examples/getting_started에 있는 파일에서 어떻게 plotting 하는지 보고 해당 헤더파일로 변경해줌

include/acado_gnuplot/gnuplot_window.hpp → acado_gnuplot.hpp

결과는 아래와 같다

sqp it | qp its |       kkt tol |       obj val |     merit val |      ls param | 
     1 |     11 |  4.015966e+01 |  9.950000e+00 |  5.419249e+01 |  1.000000e+00 | 
     2 |      1 |  1.306070e-01 |  9.931631e+00 |  1.006632e+01 |  1.000000e+00 | 
     3 |      1 |  2.549335e-02 |  9.906147e+00 |  9.906158e+00 |  1.000000e+00 | 
     4 |      1 |  7.484607e-02 |  9.831350e+00 |  9.831410e+00 |  1.000000e+00 | 
     5 |      2 |  3.457549e-01 |  9.487488e+00 |  9.489759e+00 |  1.000000e+00 | 
     6 |     12 |  3.045474e-01 |  9.190947e+00 |  9.200555e+00 |  1.000000e+00 | 
     7 |     19 |  5.194080e-01 |  8.691541e+00 |  8.715543e+00 |  1.000000e+00 | 
     8 |     14 |  4.739167e-01 |  8.248118e+00 |  8.284711e+00 |  1.000000e+00 | 
     9 |     17 |  3.334551e-01 |  7.927619e+00 |  7.943166e+00 |  1.000000e+00 | 
sqp it | qp its |       kkt tol |       obj val |     merit val |      ls param | 
    10 |     18 |  4.999093e-01 |  7.457878e+00 |  7.494079e+00 |  1.000000e+00 | 
    11 |     19 |  1.652661e-02 |  7.441887e+00 |  7.442529e+00 |  1.000000e+00 | 
    12 |     19 |  1.460624e-04 |  7.441741e+00 |  7.441741e+00 |  1.000000e+00 | 
    13 |     19 |  1.190096e-07 |  7.441741e+00 |  7.441741e+00 |  1.000000e+00 | 
 
Covergence achieved. Demanded KKT tolerance is 1.000000e-06.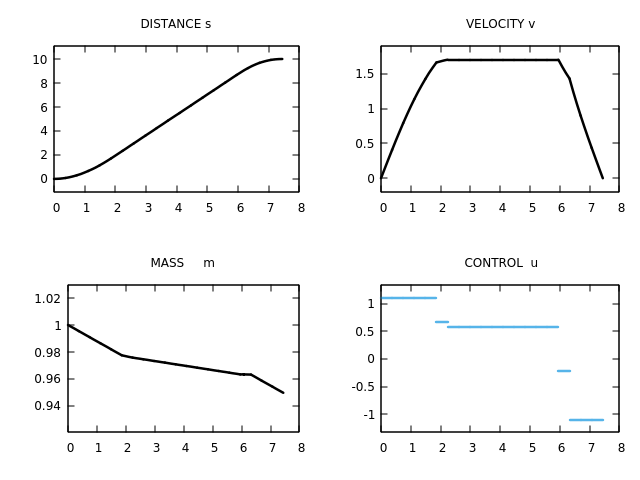

실제 튜토리얼에 나온 그래프와 동일하게 나옴.

수식은 일반적인 QP 형태라 풀어 정리할 부분은 크게 없어보이고, 코드에서 주요한 부분은 아래 파트로, 각 state에 대한 모델 equation을 <<를 통해 넣어주는 것으로 보인다.

f << dot(s) == v ;             // an implementation
f << dot(v) == (u-0.2*v*v)/m ; // of the model equations
f << dot(m) == -0.01*u*u ;     // for the rocket.

그리고 ocp.subjectTo() 함수로 state 와 control input에 대한 constraints를 넣어준다.

Tutorial의 설명에 integration 방법으로 제시된 룽게 쿠타 방법에 대해 알아보자.

Done

a Runge-Kutta method

Runge-kutta method

References

미분방정식을 크게 구분하는 상미분(ODE)와 편미분(PDE)는 의존하는 변수의 갯수로 구분된다. 즉, 상미분은 물체의 움직임을 하나의 변수로 나타낼 수 있고 편미분은 둘 이상의 변수로 표현되는 것이다.

이러한 상미분의 근사해를 구하는 수치해석 기법 중 하나가 룽게-쿠타 방법이다. 룽게-쿠타는 오일러 방식보다 Computational cost가 적으면서도 높은 정확도를 보인다.

전체 시간구간 $T$ 에 대해 시간 간격인 $Δ t$ 의 4승에 비례하는 오차를 지녀 RK4 기법으로도 불린다.

반디통에서 첨부된 이미지가 기울기 평균을 이용하는 방식을 잘 보여주는 것 같아 첨부함.

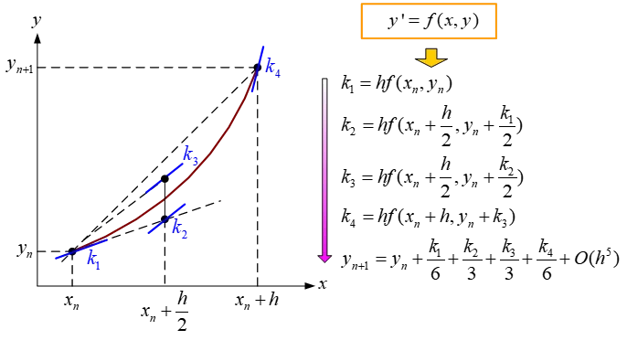
일반적인 수식에 대한 RK4 기법을 나타내보면 아래와 같다.

y^{‘} s . t = f (t, y) y (t_{0}) = y_{0}

$k 1 = f (t_{n}, y_{n})$ $k 2 = f (t_{n} + \frac{1}{2} h, y_{n} + \frac{1}{2} h k_{1})$ $k_{3} = f (t_{n} + \frac{1}{2} h, y_{n} + \frac{1}{2} h k_{2})$ $k_{4} = f (t_{n} + h, y_{n} + h k_{3})$

이렇게 계산한 k1~k4를 이용해 다음 step의 값을 예측한다.

$y_{n + 1} = y_{n} + \frac{1}{6} h (k_{1} + 2 k_{2} + 2 k_{3} + k_{4})$ $t_{n + 1} = t_{n} + h$

정리하면, 기울기를 이용해 각 구간의 값을 구하는데 시작과 끝 부분보다 중간 값에 가중치를 더 두어 이를 누적하고 평균내는 것이다.

Todo

Numerical Methods for Engineers

2번째 튜토리얼은 txt파일을 읽는 내용이고 필요할 때 찾아보면 됨.

Algorithmic Options and Numerical Accuracy

ACADO에서는 기본 설정으로 multiple-shooting SQP type method와 standard Runge-Kutta를 사용한다. 이 외에도 본인의 필요에 맞게 설정을 바꾸어 줄 수 있다.

OptimizationAlgorithm algorithm(ocp); // construct optimization algorithm,
 
algorithm.set( INTEGRATOR_TYPE , INT_RK78 );
algorithm.set( INTEGRATOR_TOLERANCE , 1e-8 );
algorithm.set( DISCRETIZATION_TYPE , SINGLE_SHOOTING );
algorithm.set( KKT_TOLERANCE , 1e-4 );
 
algorithm.solve() ; // and solve the problem.

이 전 예제에서는 첫번째와 마지막 라인만 있었다. 즉, algorithm 종류를 선언한 뒤 solve() 함수로 연산을 수행하는데, 이 사이에 set()함수로 설정을 변경해줄 수 있음.


Option Name:	Option Value:	Short Description:
MAX_NUM_ITERATIONS	int	maximum number of SQP iterations (maxNumIterations = 0: only simulation)
KKT_TOLERANCE	double	termination tolerance for the optimal control algorithm
HESSIAN_APPROXIMATION	CONSTANT_HESSIAN FULL_BFGS_UPDATE BLOCK_BFGS_UPDATE GAUSS_NEWTON EXACT_HESSIAN	constant hessian (generalized gradient method) BFGS update of the whole hessian structure exploiting BFGS update (default) Gauss-Newton Hessian approximation (only for LSQ) Exact Hessians
DISCRETIZATION_TYPE	SINGLE_SHOOTING MULTIPLE_SHOOTING COLLOCATION	single shooting discretization multiple shooting discretization (default) collocation (will be implemented soon)
INTEGRATOR_TYPE	INT_RK12 INT_RK23 INT_RK45 INT_RK78 INT_BDF	Runge Kutta integrator (adaptive Euler method) Runge Kutta integrator (order 2/3, RKF ) Runge Kutta integrator (order 4/5, Dormand Prince) Runge Kutta integrator (order 7/8, Dormand Prince) BDF (backward differentiation formula) integrator
INTEGRATOR_TOLERANCE	double	the relative tolerance of the integrator
ABSOLUTE_TOLERANCE	double	the absolute tolerance of the integrator (“ATOL”)
MAX_NUM_INTEGRATOR_STEPS	int	maximum number of integrator steps
LEVENBERG_MARQUARDT	double	value for Levenberg-Marquardt regularization
MIN_LINESEARCH_PARAMETER	double	minimum stepsize of the line-search globalization

위와 같이 지원해주는 내용을 set(<Option Name>, <Option Value>로 해주면 된다.

Storing the Results of Optimization Algorithms

ACADO에서는 알고리즘을 풀어낸 결과를 plotting하는 것 외에도 결과를 따로 저장하는 기능을 제공한다.

텍스트파일로 저장하기

// ... (IMPLEMENTATION OF THE OPTIMIZATION PROBLEM) ...
 
OptimizationAlgorithm algorithm(ocp);
algorithm.solve()                   ;
 
algorithm.getDifferentialStates("states.txt"    );
algorithm.getParameters        ("parameters.txt");
algorithm.getControls          ("controls.txt"  );

우리가 처음 코드를 작성할 때 state, control, parameters를 아래와 같이 선언을 해준다.

USING_NAMESPACE_ACADO
 
DifferentialState s,v,m ; // the differential states
Control u ; // the control input u
Parameter T ; // the time horizon T
DifferentialEquation f( 0.0, T ); // the differential

. 선언된 변수들이 OptimizationAlgorithm으로 들어가고 이를 get~으로 받아오는 방식이다.

VariablesGrid로 받아오기 Initialization of Nonlinear Optimization Algorithms 에서 생략한 내용 중 VariablesGrid로 명칭된 자료구조를 활용해 Initialization을 할 수 있었는데 마찬가지로 결과값도 이와 같은 형식으로 얻어올 수 있다
```
Variables Grid states, parameters, controls;
 
algorithm.getDifferentialStates(states    );
algorithm.getParameters        (parameters);
algorithm.getControls          (controls  );
 
states.print();
parameters.print();
controls.print();
```
. 이렇게 선언된 변수들로 다른 함수에서 사용할 수 있어, 굳이 파일을 읽어오지 않더라도 변수들을 real-time으로 받아와 사용할 수 있다.
LogRecord 로 저장하기 LogRecord는 ACADO에서 제공하는 로깅 툴로 앞선 텍스트 파일이나 콘솔 프린트 형식 외에도 여러 옵션을 설정하여 저장할 수 있는 기능이다. 자세한건 홈페이지 참고.

기본적인 내용은 모두 살펴보았고, MPC 관련 예제로 넘어가자. 앞선 Multi-Ojbective OCP(MOOCP)는 plotting이 안되거나 에러뜨는게 있어서 조금 돌려보다가 패스. Github Issues에도 아무도 관련 언급이 없었음.

Setting-Up a Process for MPC Simulations

A Guiding Example: Simulation of a Quarter Car

이번 예제에서는 MPC 시뮬레이션을 위한 셋업으로, active suspension을 가진 간단한 quarter car model을 다룬다. body와 wheel의 position, velocity를 각각 $x B, v B, x W, v W$ 로 하고 외란으로 작용하는 도로는 $R$ 로 한다. control input은 body와 wheel 사이의 damping force $F$ 로 정의하면, 아래와 같이 dynamic equation을 정의할 수 있다. 자세한 수식 유도를 찾아보고 싶었으나 state space가 딱 매칭되는 설명을 찾지 못하였음. 모델 방정식은 내가 사용하려는 것에 맞게 짜야하므로 깊게 파지 않고 패스함.

f : \overset{x}{˙}_{B} (t) \overset{x}{˙}_{W} (t) \overset{v}{˙}_{B} (t) \overset{v}{˙}_{W} (t) = v_{B} (t) v_{W} (t) \frac{1}{m _{B}} (- k_{S} x_{B} (t) + k_{S} x_{W} (t) + F (t)) \frac{1}{m _{W}} (- k_{T} x_{B} (t) - (k_{T} + k_{S}) x_{W} (t) + k_{T} R (t) - F (t))

g : (g_{1} (t) g_{2} (t)) = (x_{B} (t) 500 v_{B} (t) + F (t))

코드를 통해 수식과 매칭시켜보자.

// INTRODUCE THE VARIABLES:
// -------------------------
DifferentialState xB;
DifferentialState xW;
DifferentialState vB;
DifferentialState vW;
 
Disturbance R;
Control F;
 
Parameter mB;
double mW = 50.0;
double kS = 20000.0;
double kT = 200000.0;

위와 같이 우리가 사용하는 변수를 선언한다.

// DEFINE THE DYNAMIC SYSTEM:
// --------------------------
DifferentialEquation f;
 
f << dot(xB) == vB;
f << dot(xW) == vW;
f << dot(vB) == ( -kS*xB + kS*xW + F ) / mB;
f << dot(vW) == ( kS*xB - (kT+kS)*xW + kT*R - F ) / mW;
 
OutputFcn g;
g << xB;
g << 500.0*vB + F;
 
DynamicSystem dynSys( f,g );

그리고 ODE와 Output 함수로 Dynamic System을 선언해준다. DynamicSystem Class를 살펴보면, DifferentialEquation만 넣어주거나 DE와 OutputFcn을 같이 넣어서 Construct해줄 수 있다.

// SETUP THE PROCESS:
// ------------------
Process myProcess;
  
myProcess.setDynamicSystem( dynSys,INT_RK45 );
myProcess.set( ABSOLUTE_TOLERANCE,1.0e-8 );
  
Vector x0( 4 );
x0.setZero( );
x0( 0 ) = 0.01;

그 후 선언한 dynamic system을 intergrator와 tolerance를 설정해준다. initial state 중 $x B$ 를 0.01로 해주고 나머지는 0으로 해주기로 하였으므로 마지막 세 줄과 같이 선언.

여기까지는 Differential Equation을 풀어 Output Function을 구하기 위한 내용이다.

Setting-Up an MPC Controller

이제 이 모델에 대한 MPC 제어를 하도록 OCP를 정의해보도록 하자. Notation은 일반적인 $x, u, p, T$ 를 따른다. ( $p$ 는 time-constant 변수이다.)

Mathematical Formulation of Model Predictive Control Problems

x (\cdot), u (\cdot), p min \int_{t_{0}}^{t_{0} + T} s . t x (t_{0}) \forall t \in [t_{0}, t_{0} + T] : 0 \forall t \in [t_{0}, t_{0} + T] : 0 0 ∥ h (t, x (t), u (t), p) - η (t) ∥_{Q}^{2} d t + ∥ m (x (t_{0} + T), p, t_{0} + T) - μ ∥_{P}^{2} = x_{0} = f (t, x (t), \overset{x}{˙} (t), u (t), p) \geq s (t, x (t), u (t), p) = r (x (t_{0} + T), p, t_{0} + T)

$s$ 는 경로에 대한 constraints이고 $r$ 은 종료 시점에 대한 constraints이다.

이제 위에서 정의한 Dynamic System에 더해 Optimal control problem을 정의하고 풀어내는 코드를 살펴보자.

// DEFINE LEAST SQUARE FUNCTION:
// -----------------------------
Function h;
  
h << xB;
h << xW;
h << vB;
h << vW;
h << F;
  
// LSQ coefficient matrix
Matrix Q(5,5);
Q(0,0) = 10.0;
Q(1,1) = 10.0;
Q(2,2) = 1.0;
Q(3,3) = 1.0;
Q(4,4) = 1.0e-8;
  
// Reference
Vector r(5);
r.setAll( 0.0 );

Objective function에 넣어줄 내용을 정의한다. LSQ coefficient는 weighting factor이다. 궁금한 점은 terminal reference에 대한 내용은 튜토리얼에 왜 없는지 모르겠음. 아마도 한 time-step에 대해 control input을 구하기 때문으로 추측했음.

// DEFINE AN OPTIMAL CONTROL PROBLEM:
// ----------------------------------
const double tStart = 0.0;
const double tEnd = 1.0;
  
OCP ocp( tStart, tEnd, 20 );
  
ocp.minimizeLSQ( Q, h, r );
  
ocp.subjectTo( f );
  
ocp.subjectTo( -200.0 <= F <= 200.0 );
ocp.subjectTo( R == 0.0 );

이제 minimizeLSQ()로 weighting matrix, objective function, reference를 선언해주고 constraints를 정의해준다. 자세한 클래스 함수는 링크를 참조한다.

// SETTING UP THE REAL-TIME ALGORITHM:
// -----------------------------------
RealTimeAlgorithm alg( ocp,0.025 );
alg.set( MAX_NUM_ITERATIONS, 1 );
alg.set( PLOT_RESOLUTION, MEDIUM );
  
GnuplotWindow window;
window.addSubplot( xB, "Body Position [m]" );
window.addSubplot( xW, "Wheel Position [m]" );
window.addSubplot( vB, "Body Velocity [m/s]" );
window.addSubplot( vW, "Wheel Velocity [m/s]" );
window.addSubplot( F, "Damping Force [N]" );
window.addSubplot( R, "Road Excitation [m]" );
  
alg << window;
  
  
// SETUP CONTROLLER AND PERFORM A STEP:
// ------------------------------------
StaticReferenceTrajectory zeroReference( "ref.txt" );
  
Controller controller( alg,zeroReference );
  
Vector y( 4 );
y.setZero( );
y(0) = 0.01;
  
controller.init( 0.0,y );
controller.step( 0.0,y );

이후에는 위와 같이 알고리즘을 설정해주는데, MPC에서는 RealTimeAlgorithm 클래스로 선언하고, 최적제어 문제인 ocp와 샘플링 시간을 변수로 넣어준다. LSQ를 풀기위해 넣는 reference는 텍스트파일로 읽어서 넣어 줄 수 있다.

Controller에서 사용하는 init()함수와 step()함수는 각각 시작 시간과 initial state 벡터를 넣어주면 된다. 자세한 내용은 클래스 설명을 참고.

Performing a Basic Closed-Loop MPC Simulation

이제 MPC를 사용하는 closed-loop 형태의 시뮬레이션을 해보도록 한다.

Implementation of the MPC Simulation in ACADO

앞서 사용한 the simple quarter car model with active actuator를 사용한다.

모델에 대한 ODE 방정식을 세우고, 앞서 했던 대로 Process와 Controller을 선언해준다. 이번에는 Output Function에 별다른 수식을 넣지 않는다.

OCP를 정의하기 위한 LSQ 와 constraints도 그대로 들어간다. Controller에서는 OCP를 풀게 되고, SimulationEnvironment에는 startTime, endTime, Process, Controller를 차례로 넣어준다.

initial state를 넣고 run()하면 매 step마다의 값들을 얻을 수 있다.

Tutorial과 동일한 내용이지만 한줄 씩 따라서 작성해보았다.

Debugging

튜토리얼과 방정식들을 바탕으로 코드를 작성하였는데, 여러 에러와 문제점이 발생하였다.

우선, 튜토리얼에서 사용한 헤더파일 #include <acado_optimal_control.hpp>은 #include <acado_toolkit.hpp>로 변경되었다.

튜토리얼에서 작성한 LSQ와 constraints, solver 세팅이 코드 예제로 주어진 getting_started/simple_mpc와 상이하였다.

주요하게 다른 부분을 살펴보면

Tutorial page

Disturbance R;
Control F;
 
VariablesGrid disturbance = readFromFile( "road.txt" );;
process.setProcessDisturbance( disturbance );
 
// DEFINE LEAST SQUARE FUNCTION:
// -----------------------------
Function h;
 
h << xB;
h << xW;
h << vB;
h << vW;
h << F;

simple_mpc

Control R;
Control F;
 
// DEFINE LEAST SQUARE FUNCTION:
// -----------------------------
Function h;
 
h << xB;
h << xW;
h << vB;
h << vW;

튜토리얼에서는 Disturbance를 별도로 선언하고 VariablesGrid에도 disturbance를 선언하였다. 그리고 이를 텍스트파일로 불러와 setProcessDisturbance()로 설정해주었는데,

simple_mpc에서는 road인 $R$ 도 Control 변수로 사용하였다.

그리고 LSQ 함수의 dimension도 다르기 때문에 이후 coefficient나 reference의 dimension도 맞게 달라졌다.

Tutorials

// MPC Controller
RealTimeAlgorithm alg(ocp, 0.025);
alg.set(INTEGRATOR_TYPE, INT_RK78);
// alg.set(MAX_NUM_ITERATIONS, 2);
  
StaticReferenceTrajectory zeroReference;
Controller controller(alg, zeroReference);
  
// Simulation
SimulationEnvironment sim(0.0, 2.5, process, controller);

simple_mpc

// SETTING UP THE MPC CONTROLLER:
// ------------------------------
RealTimeAlgorithm alg( ocp,0.05 );
alg.set( MAX_NUM_ITERATIONS, 2 );
 
StaticReferenceTrajectory zeroReference;
Controller controller( alg,zeroReference );
 
// SETTING UP THE SIMULATION ENVIRONMENT, RUN THE EXAMPLE...
// ----------------------------------------------------------
SimulationEnvironment sim( 0.0,3.0,process,controller );

그리고 sampling time이나 전체 시뮬시간인 $T$ 도 상이하였다. 가장 크게 다른 것은 solver 세팅에서 튜토리얼은 INTEGRATOR_TYPE을 RK78로 하였고, simple_mpc에서는 integrator 대신 최대 iterations를 설정해주었다.

마지막으로 Tutorials

VariablesGrid diffStates;
sim.getProcessDifferentialStates(diffStates);
  
VariablesGrid feedbackControl;
sim.getFeedbackControl(feedbackControl);
  
GnuplotWindow win;
win.addSubplot(diffStates(0), "Body Position(m)");
win.addSubplot(diffStates(1), "Wheel Position(m)");
win.addSubplot(diffStates(2), "Body Velocity(m/s)");
win.addSubplot(diffStates(3), "Wheel Velocity(m/s)");

simple_mpc

VariablesGrid sampledProcessOutput;
sim.getSampledProcessOutput( sampledProcessOutput );
  
VariablesGrid feedbackControl;
sim.getFeedbackControl( feedbackControl );
  
GnuplotWindow window;
window.addSubplot( sampledProcessOutput(0), "Body Position [m]" );
window.addSubplot( sampledProcessOutput(1), "Wheel Position [m]" );
window.addSubplot( sampledProcessOutput(2), "Body Velocity [m/s]" );
window.addSubplot( sampledProcessOutput(3), "Wheel Velocity [m/s]" );

plotting을 위해 받아오는 VariablesGrid에서 튜토리얼은 getProcessDifferentialStates를 사용해서 state $x$ 를 받아왔는데, simple_mpc에서는 getSampledProcessOutput을 이용해서 받아왔다.

그래서 튜토리얼을 코드가 돌아갈 수 있도록 하여 작성해본 것과 sim_mpc, 튜토리얼 페이지에서 제공한 plot을 비교해보았다.

작성한 코드는 링크에 있다.

먼저 튜토리얼 결과

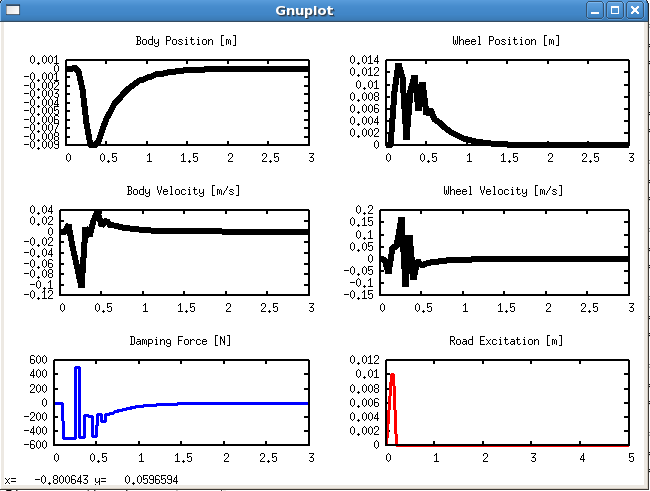
튜토리얼 코드를 현재 acado에서 돌아가도록 작성한 결과

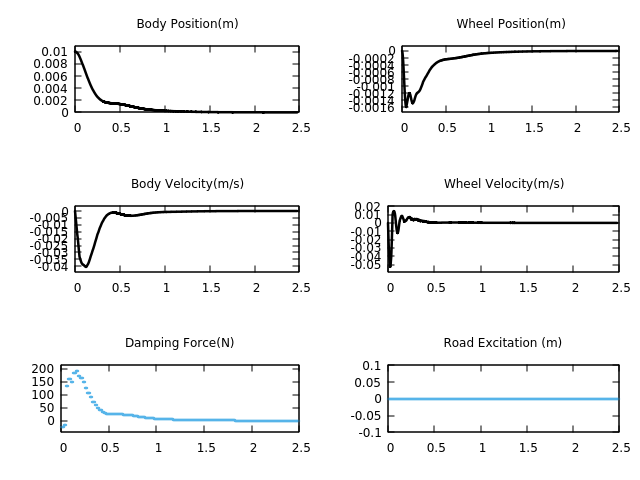
마지막으로 현재 getting_started에 있는 simple_mpc

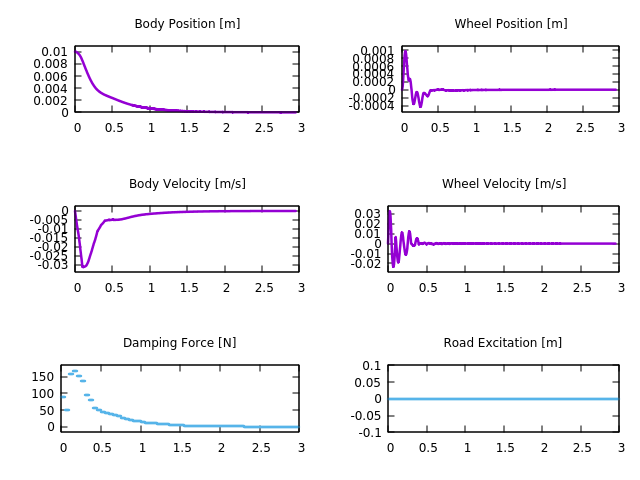
내 코드와 simple_mpc는 대부분 유사하고 $x W, v W$ 만 차이를 보인다. 아마 LSQ에 coefficient가 매우 작긴 해도 Control input인 $F$ 가 들어가 있어서 차이를 보인 것 같다. 하지만 MAX_NUM_ITERATIONS를 쓴 simple_mpc보다 INTEGRATOR_TYPE으로 RK78을 사용하며 sampling time을 더 작게 가져간 내 코드가 Body Position/Velocity인 $x B, v B$ 그래프를 보았을 때 더욱 세밀하게 나온 것을 알 수 있다.

ChanJoon

Recent notes

OpenVINS Study 2주차

Bang-bang and Bang-singular control

[T-Mech '24] SGS-Planner: A Skeleton-Guided Spatiotemporal Motion Planner for Flight in Constrained Space

Pontryagin' Minimum Principle

Mount Google Drive on Ubuntu 20.04

Ventoy

ACADO Toolkit study