Implementing MPCC with ACADO

Implementing MPCC with ACADO

Todo

Update 이전 todo로 작성한 목록들을 업데이트

• Gauss-Newton Hessian approximation
• [-] Explicit Runge-Kutta (ERK) / Implicit Runge-Kutta (IRK)
• Variational Differential Equations (VDE)
• [-] LSQ에서 coefficient matrix를 어떤 식으로 설정하는지 → coefficient matrix는 Q-norm을 QP로 바꿔주면서 각 state vector에 맞도록 생긴다.
• 전체 time horizon $T$를 linear하거나 exponential하게 고려하는 것으로 알고 있는데, 이러한 경우에 scaling을 어떻게 하는지

Goal

1. Implement Model Predictive Contouring Control(MPCC) on quadrotor with ACADO+qpOASES by referencing CMPCC
2. Experiment MPCC on ROS by using the source code of PAMPC

Differences between each papers(MPC or MPCC on quadrotor)

	CMPCC	PAMPC	MPCC	Ours
OCP	MPCC	MPC	MPCC	MPCC
Solver	OSQP	ACADO	ACADO	ACADO
code	open(GPLv3)	open(GPLv3)	None
ODE	No	Yes	Yes	Yes

As we can see above, the easiest way of implementing MPCC is migration solver of CMPCC to ACADO. But CMPCC does not consider quadrotor dynamic model on their control. the MPCC paper considered quadrotor dynamic model well, and they used ACADO for experiments. but they didn’t open their source code.

So based on CMPCC, we need to reformulate optimal control problem and the cost function of MPCC.

Brief Summarization of CMPCC

the Objective function

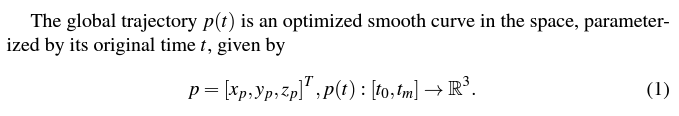
By introducing re-timing function $t(\tau )$, minimize tracking error between global trajectory $p(t)$ and local trajectory $s(\tau )$.

the System

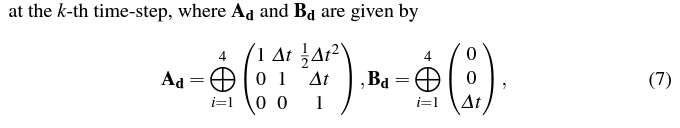
They used 3rd-order integral model instead of general quadrotor dynamic model.

The state and inputs of the system is given by

$$\begin{array}{c}\text{x}=[x,v_x,a_x,y,v_y,a_y,z,v_z,a_z,t,v_t,a_t{]}^T\\ \text{u}=[{\dot{J}}_x,{\dot{J}}_y,{\dot{J}}_z,{\dot{J}}_t{]}^T\end{array}$$

With linear state-transfer equation, they update their 3rd-oder inegral model to the next time step.

$$x^{(k+1)}=\left[\begin{array}{ccccc}{A}_{d1}& & & & \\ & A_{d2}& & & \\ & & A_{d3}& & \\ & & & A_{d4}& \end{array}\right]{\left[\begin{array}{c}x\\ v_x\\ a_x\\ y\\ v_y\\ a_y\\ z\\ v_z\\ a_z\\ t\\ v_t\\ a_t\end{array}\right]}^{(k)}+\left[\begin{array}{ccccc}& & & & \\ & & & & \\ \Delta t& & & & \\ & & & & \\ & & & & \\ & \Delta t& & & \\ & & & & \\ & & & & \\ & & & & \\ & & \Delta t& & \\ & & & & \\ & & & & \\ & & & \Delta t& \end{array}\right]{\left[\begin{array}{c}{\dot{J}}_x\\ {\dot{J}}_y\\ {\dot{J}}_z\\ {\dot{J}}_t\end{array}\right]}^{(k)}={\left[\begin{array}{c}x+\Delta t\cdot v_x+\frac{1}{2}\Delta t^2\cdot a_x\\ v_x+\Delta t\cdot a_x\\ a_x+\Delta t\cdot \dot{J_x}\\ y+\Delta t\cdot v_y+\frac{1}{2}\Delta t^2\cdot a_y\\ v_y+\Delta t\cdot a_y\\ a_y+\Delta t\cdot \dot{J_y}\\ z+\Delta t\cdot v_z+\frac{1}{2}\Delta t^2\cdot a_z\\ v_z+\Delta t\cdot a_z\\ a_z+\Delta t\cdot \dot{J_z}\\ t+\Delta t\cdot v_t+\frac{1}{2}\Delta t^2\cdot a_t\\ v_t+\Delta t\cdot a_t\\ a_t+\Delta t\cdot \dot{J_t}\end{array}\right]}^{(k)}=\left[\begin{array}{c}{x}^{(k+1)}\\ v_x^{(k+1)}\\ a_x^{(k+1)}\\ y^{(k+1)}\\ v_y^{(k+1)}\\ a_y^{(k+1)}\\ z^{(k+1)}\\ v_z^{(k+1)}\\ a_z^{(k+1)}\\ t^{(k+1)}\\ v_t^{(k+1)}\\ a_t^{(k+1)}\end{array}\right]$$

OCP Formulation

Most of MPCC suffers from getting the reference state of global trajectory ${\mu }_p(t^{(k)})$. They solved this problem by introducing the equation (9) which linearizes ${\mu }_p(t^{(k)})$ using the result of the last horizon $t^{(k+1)}$.

Detailed expansions from the equation (8) to (10) as follows.

$$\begin{array}{rl}J& =\sum _{k=1}^N\{({\mu }^{(k)}-{\mu }_p(t^{(k)}){)}^2-\rho \cdot v_t^{(k)}\}\\ & =\sum _{k=1}^N\{({\mu }^{(k)}-{\mu }_p({\theta }^{(k)})-v_p({\theta }^{(k)})\cdot (t^{(k)}-{\theta }^{(k)}){)}^2-\rho \cdot v_t^{(k)}\}\\ & =\sum _{k=1}^N\{f^{(k)}\}\end{array}$$

and convert $f^{(k)}$ to $x^{T}Qx$ form which is widely used in Quadratic Programming(QP).

$$\begin{array}{rl}{f}^{(k)}& =\{{\mu }^{(k)}-{\mu }_p({\theta }^{(k)})-v_p({\theta }^{(k)})\cdot (t^{(k)}-{\theta }^{(k)}){\}}^2-\rho \cdot v_t^{(k)}\\ & ={\mu }^2-2\mu {\mu }_p(\theta )+{\mu }_p^2(\theta )-2\mu v_p(\theta )(t-\theta )+2{\mu }_p(\theta )v_p(\theta )(t-\theta )+v_p^2(\theta )(t-\theta {)}^2-\rho \cdot v_p\\ & ={\left[\begin{array}{c}\mu \\ 1\end{array}\right]}^T\left[\begin{array}{cc}1& -v_p(\theta )(t-\theta )\\ -v_p(t-\theta )& v_p^2(\theta )(t-\theta {)}^2\end{array}\right]+{\left[\begin{array}{c}-2v_p(\theta )\\ {\mu }_p^2(\theta )+2{\mu }_p(\theta )v_p(\theta )(t-\theta )-\rho \cdot v_t\end{array}\right]}^T\left[\begin{array}{c}\mu \\ 1\end{array}\right]\\ & ={\left[\begin{array}{c}\mu \\ t\end{array}\right]}^T\left[\begin{array}{cc}1& -v_p(\theta )\\ -v_p(\theta )& v_p^2(\theta )\end{array}\right]\left[\begin{array}{c}\mu \\ t\end{array}\right]+{\left[\begin{array}{c}-2{\mu }_p(\theta )+2v_p(\theta )\cdot \theta \\ v_p^2(\theta )(-2t\cdot \theta +{\theta }^2)+{\mu }_p^2(\theta )+2{\mu }_p(\theta )v_p(\theta )(t-\theta )-2{\mu }_p{v}_p\cdot \theta -\rho \cdot v_t\end{array}\right]}^T\left[\begin{array}{c}\mu \\ 1\end{array}\right]\\ & ={\left[\begin{array}{c}\mu \\ t\end{array}\right]}^T\left[\begin{array}{cc}1& -v_p(\theta )\\ -v_p(\theta )& v_p^2(\theta )\end{array}\right]\left[\begin{array}{c}\mu \\ t\end{array}\right]+{\left[\begin{array}{c}2(-{\mu }_p(\theta )+v_p(\theta )\cdot \theta )\\ -2v_p(\theta )(-{\mu }_p(\theta )+v_p(\theta )\cdot \theta )\\ -\rho \end{array}\right]}^T\left[\begin{array}{c}\mu \\ t\\ v_t\end{array}\right]\end{array}$$

this paper skips $({\mu }_p(\theta )-v_p(\theta )\cdot \theta {)}^2$(may be consider as 0) and select $x,y,z$ in $\mu$.

Now we can rearrange $J={\sum }_{k=1}^N{f}^{(k)}={\sum }_{k=1}^N{\bar{\text{x}}}^T{Q}_k\bar{\text{x}}+q_k^T\bar{\text{x}}$ by selecting $\bar{\text{x}}=\left[\begin{array}{ccccc}x& y& z& t& v_t\end{array}\right]$

---

Eigen::Matrix<float, kCostSize-kStateSize, kSamples>::Zero();
kCostSize-kStateSize = -13; // kCostSize = 5, kStateSize = 13;