Pontryagin' Minimum Principle

Pontryagin’s Minimum Principle

Quote

The structure of a transition maneuver is obtained by Pontryagin’s minimum principle and then a numerical algorithm is proposed to solve the boundary value problem induced by the minimum principle to compute maneuvers for arbitrary initial and final states.

M. Fässler, “Quadrotor control for accurate agile flight,” University of Zurich, 2018. doi: 10.5167/UZH-152425.

참고한 Thesis 외에도 여러 최적제어 논문들에서 언급되는 Pontryagin’s minimum principle 에 대해 알아보도록 하자.

What is Pontryagin’s minimum principle(PMP)?

Pontryagin’s Minimum Principle(PMP)은 제어 이론에서 Hamiltonian을 최소화하는 방식으로 사용되어, 종종 Pontryagin’s Maximum Principle로도 불리지만 일반적으로는 PMP로 더 잘 알려져 있다. PMP는 무한 차원을 갖는 Optimal Control Problem(OCP) 을 직접 해결하는 것보다, Hamiltonian을 최소화하거나 최대화하는 방식이 더 간단하다는 점에서 도입된다.

PMP는 최적 제어 문제에서 최적 해의 필요 조건을 제공하지만, 최적 해의 충분 조건은 아니다. 이는 PMP가 최적 해를 직접적으로 제공하는 것은 아니지만, 최적이 될 수 없는 경우를 배제할 수 있는 도구로 작용한다. 즉, Hamiltonian을 최소화하지 못하는 제어 입력은 최적이 아니며, 이를 통해 최적 제어 입력의 범위를 좁힐 수 있다.

반면, Hamilton-Jacobi-Bellman(HJB) 방정식은 전체 상태 공간에서 최적의 cost-to-go와 optimal policy를 제공하여, 필요충분 조건을 만족하는 최적 해를 구할 수 있다. 하지만 HJB는 상태 공간 전체에서 방정식을 해결해야 하므로 계산이 매우 복잡하고 비용이 많이 든다. 이에 비해, PMP는 특정 궤적에서만 필요 조건을 만족하면 되기 때문에 계산적으로 더 간편하고 효율적일 수 있다.

Note

• 간단히 수식적으로 표현하면 $\delta J(u^{\ast },\delta u)=0$ 를 만족하는 제어 입력을 구하는 대신 $\delta J(u^{\ast },\delta u)\ge 0$ 를 만족하는 제어 입력을 찾는 것.

Notation

Lemma *Let $F(t,x,u)$ be a continuously differentiable function of $t\in \mathbb{R},x\in {\mathbb{R}}^n,u\in {\mathbb{R}}^m$ and let $\mathcal{U}\subset {\mathbb{R}}^m$ be a convex set. Furthermore, assume ${\mu }^{\ast }(t,x):=\arg {\min }_{u\in \mathcal{U}}F(t,x,u)$ exists and is continuously differentiable. Then for all $t$ and $x$, *

$$\begin{array}{rl}\frac{\partial ({\min }_{u\in \mathcal{U}}F(t,x,u))}{\partial t}& =\frac{\partial F(t,x,u)}{\partial t}{|}_{u={\mu }^{\ast }(t,x)}\\ \frac{\partial ({\min }_{u\in \mathcal{U}}F(t,x,u))}{\partial x}& =\frac{\partial F(t,x,u)}{\partial x}{|}_{u={\mu }^{\ast }(t,x)}\end{array}$$

Proof. We prove this for when $\mathcal{U}\in {\mathbb{R}}^m$. Let $G(t,x):={\min }_{u\in \mathcal{U}}F(t,x,u)=F(t,x,{\mu }^{\ast }(t,x)$. Then,

$$\frac{\partial G(t,x)}{\partial t}=\frac{\partial F(t,x,{\mu }^{\ast }(t,x))}{\partial t}=\frac{\partial F(t,x,u)}{\partial t}{|}_{u={\mu }^{\ast }(t,x)}+\frac{\partial F(t,x,u)}{\partial u}{|}_{u={\mu }^{\ast }(t,x)}\frac{\partial {\mu }^{\ast }(t,x)}{\partial t}$$

이와 같이 $x$ 에 관해서도 편미분을 보일 수 있다.

위 Lemma 이 어떤 의미인지 아래 예제를 살펴보자.

Example

Let $F(t,x,u):=(1+t)u^2+ux+1,t\ge 0$. Then,

$$\underset{u\in \mathbb{R}}{\min }F(t,x,u):2(1+t)u+x=0,u=-\frac{x}{2(1+t)}$$ $$\therefore {\mu }^{\ast }(t,x)=-\frac{x}{2(1+t)}$$ $$\therefore \underset{u\in \mathbb{R}}{\min }F(t,x,u)=\frac{(1+t)x^2}{4(1+t{)}^2}-\frac{x^2}{2(1+t)}+1=-\frac{x^2}{4(1+t)}+1$$

이 예제를 우선 $t$ 에 관해 미분해보자.

$$\frac{\partial ({\min }_{u\in \mathbb{R}}F(t,x,u))}{\partial t}=\frac{\partial F(t,x,{\mu }^{\ast }(t,x))}{\partial t}=\frac{x^2}{4(1+t{)}^2}$$

그리고 Lemma 을 적용해보면 위와 같게 나오는 것을 알 수 있다.

$$\begin{array}{rl}\frac{\partial ({\min }_{u\in \mathbb{R}}F(t,x,u))}{\partial t}& =\frac{\partial F(t,x,u)}{\partial t}{|}_{u={\mu }^{\ast }(t,x)}\\ & =u^2{|}_{u=-\frac{x}{2(1+t)}}\\ & =\frac{x^2}{4(1+t{)}^2}\end{array}$$

그리고 $x$ 에 관해 미분하는 경우도 만족함을 알 수 있다.

$$\frac{\partial ({\min }_{u\in \mathbb{R}}F(t,x,u))}{\partial x}=\frac{\partial F(t,x,{\mu }^{\ast }(t,x))}{\partial x}=-\frac{x}{2(1+t)}$$

마찬가지로 Lemma 10.1 을 적용한 경우에도 아래와 같이 만족한다.

$$\begin{array}{rl}\frac{\partial ({\min }_{u\in \mathbb{R}}F(t,x,u))}{\partial x}& =\frac{\partial F(t,x,u)}{\partial x}{|}_{u={\mu }^{\ast }(t,x)}\\ & =u{|}_{u=-\frac{x}{2(1+t)}}\\ & =-\frac{x}{2(1+t)}\end{array}$$

The Principle

이제 PMP 를 수식적으로 알아보자.

Dynamics

time $t\in {\mathbb{R}}_{\ge 0}$ 와 state $x(t)\in \mathcal{S}:={\mathbb{R}}^n,\forall t\in [0,T]$, control $u(t)\in \mathcal{U}\subset {\mathbb{R}}^m,\forall t\in [0,T]$ 라고 하자. 이 때, $\mathcal{U}$ 는 control constraint set 이다.

$$\dot{x}(t)=f(x(t),u(t)),0\le t\le T$$

Cost

$$h(\mathbf{x}(t_f),t_f)+{\int }_{t_0}^{t_f}g(\mathbf{x}(t),\mathbf{u}(t),t)dt$$

종단 시점 $T$ 에서의 cost function $h$ 와 $t\in [0,T]$ 에서의 cost function $g$ 를 통해 위와 같이 일반적으로 표현할 수 있다.

Objective

따라서 이러한 system dynamics 를 고려하였을 때 OCP 를 아래와 같이 정의할 수 있다.

$$\begin{array}{rl}\min J(\mathbf{u}(t))& =h(\mathbf{x}(t_f),t_f)+{\int }_{t_0}^{t_f}g(\mathbf{x}(t),\mathbf{u}(t),t)dt\\ \text{subject to}\dot{\mathbf{x}}(t)& =f(\mathbf{x}(t),\mathbf{u}(t),t)\end{array}$$

여기서 $f,g,h$ 는 모두 $\mathbf{x}$ 에 대해 연속적이고 미분가능하다.

이러한 OCP 는 HJB 를 통해 ${\mu }^{\ast }(t,x)$ 를 얻을 수도 있지만 일반적으로는 이러한 방식을 사용하기 어렵다.

Theorem

For a given initial condition $x(0)=\mathbf{x}\in \mathcal{S}$, let $u(t)$ be an optimal control trajectory with associated state trajectory $x(t)$ for the system $\text{(10.1)}$. Then there exists a trajectory $p(t)$ such that:

$$\begin{array}{rl}\dot{p}(t)& =-\frac{\partial H(x,u,p)}{\partial x}{|}_{x(t),u(t),p(t)}^{⊺},p(T)=\frac{\partial h(x)}{\partial x}{|}_{x(T)}^{⊺}\\ u(t)& =\arg \underset{u\in \mathcal{U}}{\min }H(x(t),u,p(t))\\ H(x(t),u(t),p(t))& =\text{constant}\forall t\in [0,T]\\ \text{where}H(x,u,p):=g(x,& u)+p^{⊺}f(x,u).\end{array}$$

여기서의 $H(\cdot ,\cdot ,\cdot )$ 은 Hamiltonian 이다.

Proof.

HJB & Hamiltonian 연결

$$0=\underset{u\in \mathcal{U}}{\min }\underset{=:F(t,x,u)}{\underbrace{(g(x,u)+\frac{\partial J(t,x)}{\partial t}+\frac{\partial J(t,x)}{\partial x}f(x,u))}}$$

• 위의 HJB 방정식에 Hamiltonian 을 도입하여 계산가능한 문제로 변환시킬 것임.
• 이를 통해 HJB 최소화 문제를 Hamiltonian 최소화 문제로 변환하여 최적 제어입력 $u(t)$ 를 유도할 것임.

증명에 앞서 목적함수 $J(t,x)$ 와 최적 policy $\mu (\cdot ,\cdot )$ 모두 연속하고 미분가능하다. 또한, Lemma 10.1 을 위해 $\mathcal{U}$ 는 convex 하다.

연속이고 미분가능한 $J$ 에 대해 HJB 는 최적해의 필요조건이다.

$$\begin{array}{rl}0& =\underset{u\in \mathcal{U}}{\min }\underset{=:F(t,x,u)}{\underbrace{(g(x,u)+\frac{\partial J(t,x)}{\partial t}+\frac{\partial J(t,x)}{\partial x}f(x,u))}},\forall t\in [0,T],\forall x\in \mathcal{S}\\ & =\underset{u\in \mathcal{U}}{\min }F(t,x,u)\\ J(T,x)& =h(x),\forall x\in \mathcal{S}\end{array}\text{\hspace{1em}(1)}$$

수식 (1) 을 $t$ 와 $x$ 에 대해 각각 미분하고, Lemma 를 적용해보자.

$$\begin{array}{rl}0& =\frac{\partial ({\min }_{u\in \mathcal{U}}F(t,x,u))}{\partial t}=\frac{\partial F(t,x,u)}{\partial t}{|}_{\mu (t,x)}\\ & =\frac{{\partial }^{2}J(t,x)}{\partial t^2}+\frac{{\partial }^{2}J(t,x)}{\partial t\partial x}f(x,\mu (t,x))\end{array}\text{\hspace{1em}(2)}$$ $$\begin{array}{rl}0& =\frac{\partial ({\min }_{u\in \mathcal{U}}F(t,x,u))}{\partial x}=\frac{\partial F(t,x,u)}{\partial x}{|}_{\mu (t,x)}\\ & =\frac{\partial g(x,u)}{\partial x}{|}_{\mu (t,x)}+\frac{{\partial }^{2}J(t,x)}{\partial x\partial t}+f(x,\mu (t,x){)}^{⊺}\frac{{\partial }^{2}J(t,x)}{\partial x^2}+\frac{\partial J(t,x)}{\partial x}\frac{\partial f(x,u)}{\partial x}{|}_{\mu (t,x)}\end{array}\text{\hspace{1em}(3)}$$

우리는 다음과 같은 조건을 만족하는 optimal trajectory $u(t):=\mu (t,x(t))$ 를 얻고자 한다.

Conditions

$$\begin{array}{rl}\dot{x}& =f(x(t),u(t))={\frac{\partial H(x,u,p)}{\partial p}}^{⊺}{|}_{x(t),u(t)}\\ x(0)& =\mathbf{x}\end{array}$$

이를 만족하도록 수식 (2-3) 을 다시 적어보자.

$$\begin{array}{rl}0& =\frac{{\partial }^{2}J(t,x)}{\partial t^2}{|}_{x(t)}+\frac{{\partial }^{2}J(t,x)}{\partial t\partial x}{|}_{x(t)}\dot{x}(t)\\ & =\frac{d}{dt}\left(\underset{=:r(t)}{\underbrace{\frac{\partial J(t,x)}{\partial t}}}\right)\\ 0& =\frac{\partial g(x,u)}{\partial x}{|}_{x(t),u(t)}+\frac{{\partial }^{2}J(t,x)}{\partial x\partial t}{|}_{x(t)}+\dot{x}(t{)}^{⊺}\frac{{\partial }^{2}J(t,x)}{\partial x^2}{|}_{x(t)}+\frac{\partial J(t,x)}{\partial x}{|}_{x(t)}\frac{\partial f(x,u)}{\partial x}{|}_{x(t),u(t)}\\ & =\frac{\partial g(x,u)}{\partial x}{|}_{x(t),u(t)}+\frac{d}{dt}\left(\underset{=:p(t{)}^{⊺}}{\underbrace{\frac{\partial J(t,x)}{\partial x}}}\right)+\frac{\partial J(t,x)}{\partial x}{|}_{x(t)}\frac{\partial f(x,u)}{\partial x}{|}_{x(t),u(t)}\end{array}\text{\hspace{1em}(4)(5)}$$

Derivation of Equation (5)

• 다변수 함수의 미분은 모든 변수를 고려하므로 chain rule 을 적용한다.

$$\frac{dJ(t,x(t))}{dt}=\frac{\partial J(t,x)}{\partial t}+\frac{\partial J(t,x)}{\partial x}\cdot \frac{dx(t)}{dt}$$

• 따라서 수식 (5)의 유도에서 두 번째 텀과 세 번째 텀을 합쳐서 $\frac{d}{dt}(\frac{\partial J(t,x)}{\partial x})$ 로 표현한 것이다.

$r(t):=\frac{\partial J(t,x)}{\partial t}{|}_{x(t)}$ 로 표현하면 수식 (4) 는 아래와 같이 정리된다.

$$\dot{r}(t)=0\Rightarrow r(t)=\text{constant}\forall t$$

그리고 trajectory(=co-state) $p(t):=\frac{\partial J(t,x)}{\partial x}{|}_{x(t),u(t)}^T$ 로 두면 수식 (5) 는 아래와 같이 정리된다.

$$\begin{array}{rl}\dot{p}(t)& =-\frac{\partial g(x,u)}{\partial x}{|}_{x(t),u(t)}^{⊺}-\frac{\partial f(x,u)}{\partial x}{|}_{x(t),u(t)}^{⊺}p(t)\\ & =-\frac{\partial H(\mathbf{x},\mathbf{u},\mathbf{p})}{\partial \mathbf{x}}{|}_{x(t),u(t),p(t)}^{⊺}\end{array}$$

Boundary condition 으로 주어진 수식 (1) 은 cost-to-go $J$ 가 종단 시점 $T$ 에서 최종 시점의 cost 인 $h$ 와 동일하게 만들어주는 것이다.

이를 $x$ 에 대해 편미분을 취하면 $\frac{\partial J(T,x)}{\partial x}=\frac{\partial h(x)}{\partial x},\forall x\in \mathcal{S}$ 가 되고 이는 아래와 같이 정리된다.

$$p(T)=\frac{\partial J(T,x)}{\partial x}{|}_{T,x(T)}^{⊺}=\frac{\partial h(x)}{\partial x}{|}_{x(T)}^{⊺}$$

수식 (1) 을 정리해서 다음과 같이 Bellman 의 최적성 원리 에서 Hamiltonian 을 이용한 수식으로 표현할 수 있다.

$$\begin{array}{rl}0& =\underset{u\in \mathcal{U}}{\min }\underset{=:F(t,x,u)}{\underbrace{(g(x,u)+\frac{\partial J(t,x)}{\partial t}+\frac{\partial J(t,x)}{\partial x}f(x,u))}}\\ -\frac{\partial J(t,x)}{\partial t}& =\underset{u\in \mathcal{U}}{\min }(g(x,u)+\frac{\partial J(t,x)}{\partial x}f(x,u))\\ & =\underset{u\in \mathcal{U}}{\min }H(x,u,{\frac{\partial J(t,x)}{\partial x}}^{⊺})\end{array}$$

따라서 다음과 같은 optimal trajectory 을 얻음을 알 수 있다.

$$-r(t)=H(x(t),u(t),p(t))=\text{constant}$$

그리고 optimal control input $u(t)$ 는 아래와 같다.

$$\begin{array}{rl}u(t)& =\arg \underset{u\in \mathcal{U}}{\min }F(t,x(t),u)\\ & =\arg \underset{u\in \mathcal{U}}{\min }(g(x(t),u)+\frac{\partial J(t,x)}{\partial x}{|}_{x(t)}f(x(t),u))\\ & =\arg \underset{u\in \mathcal{U}}{\min }(g(x(t),u)+p(t{)}^{⊺}f(x(t),u))\\ & =\arg \underset{u\in \mathcal{U}}{\min }H(x(t),u,p(t))\end{array}$$

Examples

Minimum Time Control

아래와 같은 선형 시스템의 상태방정식을 고려해보자.

$$\dot{x}=Ax+Bu$$

이 때의 목적함수를 표현해보자.

$$\begin{array}{rl}\min J& ={\int }_{t_0}^{t_f}dt\\ \text{subject to}\dot{x}& =Ax+Bu\\ |u|& \le u_{max}\end{array}$$

이 때의 $H,p$ 를 통해 최적 제어 조건을 알아보고 $u^{\ast }$ 를 구하자.

$$\begin{array}{rl}\text{Hamiltonian}H& =1+p^T[Ax+Bu]\\ \text{Co-state}\dot{p}& =-{\frac{\partial H}{\partial x}}^{⊺}=-A^{⊺}p\\ \text{State}\dot{x}& =\frac{\partial H}{\partial p}=Ax+Bu\\ \text{Optimal condition}& \\ H(x^{\ast },u^{\ast },p^{\ast },t)& \le H(x^{\ast },u^{\ast }+\delta u,p^{\ast },t)\\ p^{T}B{u}^{\ast }& \le p^{T}Bu\end{array}$$ $$p^{⊺}Bu=\left[\begin{array}{cccc}{p}^T{b}_1& p^T{b}_2& \dots & p^T{b}_m\end{array}\right]\left[\begin{array}{c}u1\\ u2\\ ⋮\\ u_m\end{array}\right]$$

따라서 최적 제어입력 $u^{\ast }$ 는 아래와 같이 결정된다.

$$\begin{array}{r}{u}^{\ast }=\left[\begin{array}{c}{u}_1^{\ast }\\ u_2^{\ast }\\ ⋮\\ u_m^{\ast }\end{array}\right]\end{array}$$ $$\begin{array}{r}\text{where}{u}_i^{\ast }=\{\begin{array}{ll}-sign(p^T{b}_i)|u_{max,i}|& p^T{b}_i\ne 0\\ \text{undetermined}& p^T{b}_i=0\end{array}\end{array}$$

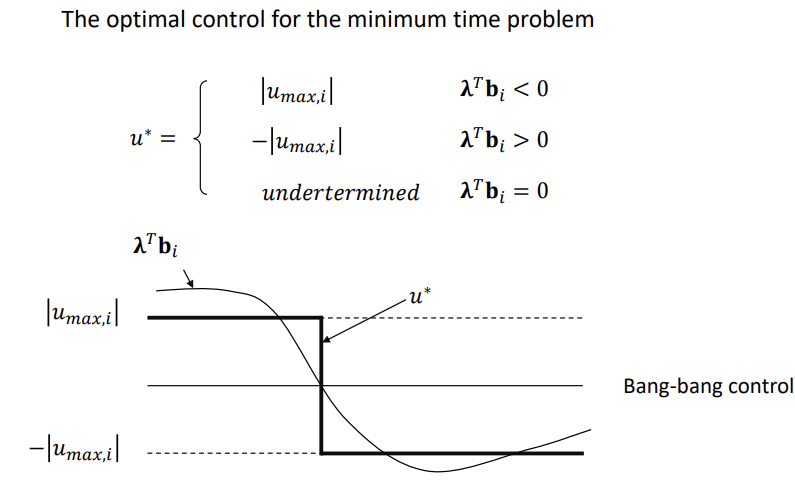
추가적인 예제는 KOCW 최적제어 이론의 10강 PDF 에서 더 확인해볼 수 있다.

References

.

• Lecture 10: Pontryagins Minimum Principle
• KOCW 최적제어이론
• Ch 15.2.3 of Planning Algorithms by Steven M. LaValle (p.g 875~879)
• ECE276B: Planning & Learning in Robotics